2.14　求数组的子数组之和的最大值

一个有N个整数元素的一维数组（A[0]，A[1]，…，A[n－2]，A[n－1]），这个数组当然有很多子数组，那么子数组之和的最大值是什么呢？

这是一道看似简单，实际上也挺简单，但是却难倒了不少学生的题目。这也是很多公司面试的题目，微软亚洲研究院曾在2006年的笔试题中出过这道题，只有20％的人能够写出正确的解法，能做到最优O（N）解法的同学非常少。事实上这个题目及相关解答在网上都能够找到，不过散布于网上的几个版本似乎都有不正确的地方，我们在这里总结一下。

分析与解法

【解法一】

我们先明确题意：

1．题目说的子数组，是连续的。

2．题目只需要求和，并不需要返回子数组的具体位置。

3．数组的元素是整数，所以数组可能包含有正整数、零、负整数。

举几个例子：

数组：[1，-2，3，5，-3，2]应返回：8

数组：[0，-2，3，5，-1，2]应返回：9

数组：[-9，-2，-3，-5，-3]应返回：-2，这也是最大子数组的和。

这几个典型的输入能帮助我们测试算法的逻辑。在写具体算法前列出各种可能输入，也可以让应聘者有机会和面试者交流，明确题目的要求。例如：如果数组中全部是负数，怎么办？是返回0，还是最大的负数？这是面试和闭卷考试不一样的地方，要抓住机会交流。

了解了题意之后，我们试验最直接的方法，记Sum[i，…，j]为数组A中第i个元素到第j个元素的和（其中0＜＝i＜＝j＜n），遍历所有可能的Sum[i，…，j]，那么时间复杂度为O（N³）：

代码清单2-24

如果注意到Sum[i，…，j]＝Sum[i，…，j－1]＋A[j]，则可以将算法中的最后一个for

循环省略，避免重复计算，从而使得算法得以改进，改进后的算法如下，这时复杂度为O（N²）：

代码清单2-25

能继续优化吗？

【解法二】

如果将所给数组（A[0]，…，A[n－1]）分为长度相等的两段数组（A[0]，…，A[n/2－1]）和（A[n/2]，…，A[n－1]），分别求出这两段数组各自的最大子段和，则原数组（A[0]，…，A[n－1]）的最大子段和为以下三种情况的最大值：

1．（A[0]，…，A[n－1]）的最大子段和与（A[0]，…，A[n/2－1]）的最大子段和相同。

2．（A[0]，…，A[n－1]）的最大子段和与（A[n/2]，…，A[n－1]）的最大子段和相同。

3．（A[0]，…，A[n－1]）的最大子段跨过其中间两个元素A[n/2－1]到A[n/2]。

1和2两种情况事实上是问题规模减半的相同子问题，可以通过递归求得。

至于第3种情况，我们只要找到以A[n/2－1]结尾的和最大的一段数组和s₁＝（A[i]，…，A[n/2－1]）（0＜＝i＜n/2－1）A[]和以A[n/2]开始和最大的一段和s₂＝（A[n/2]，…，A[j]）（n/2＜＝j＜n）。那么第3种情况的最大值为s₁＋s₂＝A[i]＋…＋A[n/2－1]＋A[n/2]＋…＋A[j]，只需要对原数组进行一次遍历即可。

其实这是一种分治算法，每个问题都可分解成为两个问题规模减半的子问题，再加上一次遍历算法。该分治算法的时间复杂度满足典型的分治算法递归式，总的时间复杂度为T（n）＝O（n*log₂N）。

【解法三】

解法二中的分治算法已经将时间复杂度从O（N²）降到了O（n*log₂N），应该说是一个不错的改进，但是否还可以进一步将时间复杂度降低呢？答案是肯定的，从分治算法中得到提示：可以考虑数组的第一个元素A[0]，以及最大的一段数组（A[i]，…，A[j]）跟A[0]之间的关系，有以下几种情况：

1．当0＝i＝j时，元素A[0]本身构成和最大的一段；

2．当0＝i＜j时，和最大的一段以A[0]开始；

3．当0＜i时，元素A[0]跟和最大的一段没有关系。

从上面三种情况可以看出，可以将一个大问题（N个元素数组）转化为一个较小的问题（n－1个元素的数组）。假设已经知道（A[1]，…，A[n－1]）中和最大的一段之和为All[1]，并且已经知道（A[1]，…，A[n－1]）中包含A[1]的和最大的一段的和为Start[1]。那么，根据上述分析的三种情况，不难看出（A[0]，…，A[n－1]）中问题的解All[0]是三种情况的最大值max{A[0]，A[0]＋Start[1]，All[1]}。通过这样的分析，可以看出这个问题符合无后效性，可以使用动态规划的方法来解决。

代码清单2-26

新方法的时间复杂度已经降到O（N）了。

但一个新的问题出现了：我们又额外申请了两个数组All[]、Start[]，能否在空间方面也节省一点呢？

观察这两个递推式：

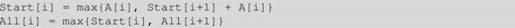
第一个递推式：Start[i]＝max{A[i]，Start[i＋1]＋A[i]}。如果Start[i＋1]＜0，则Start[i]＝A[i]。而且，在这两个递推式中，其实都只需要用两个变量就可以了。Start[k＋1]只有在计算Start[k]时使用，而All[k＋1]也只有在计算All[k]时使用。所以程序可以进一步改进一下，只需O（1）的空间就足够了。

代码清单2-27

改进的算法不仅节省了空间，而且只有寥寥几行，却达到了很高的效率，是不是很美呢？

我们还可以换一个写法：

代码清单2-28

扩展问题

1．如果数组（A[0]，…，A[n－1]）首尾相邻，也就是我们允许找到一段数字（A[i]，…，A[n－1]，A[0]，…，A[j]），请使其和最大，怎么办？

可以把问题的解分为两种情况：

（1）解没有跨过A[n－1]到A[0]（原问题）。

（2）解跨过A[n－1]到A[0]。

对于第二种情况，只要找到从A[0]开始和最大的一段（A[0]，…，A[j]）（0＜＝j＜n），以及以A[n－1]结尾的和最大的一段（A[i]，…，A[n－1]）（0＜＝i＜n），那么，第二种情况中，和的最大值M_2为：

M_2＝A[i]＋…＋A[n－1]＋A[0]＋…＋A[j]

如果i＞j，则

M_2＝A[0]＋…＋A[n－1]

否则

M_2＝A[0]＋…＋A[j]＋A[i]＋…＋A[n－1]

最后，再取两种情况的最大值就可以了，求解跨过A[n－1]到A[0]的情况只需要遍历数组一次，故总的时间复杂度为O（N）＋O（N）＝O（N）。

2．如果题目要求同时返回最大子数组的位置，算法应如何改变？还能保持O（N）的时间复杂度么？