1.15　构造数独

数独（日语：数独，sudoku）是一个历史悠久，最近又特别流行的数学智力游戏。它不仅具有很强的趣味性，而且能锻炼我们的逻辑思维能力。数独的“棋盘”是由九九八十一个小方格组成的。玩家要在每一个小格中，分别填上1至9的任意一个数字，让整个棋盘每一列、每一行以及每一个3×3的小矩阵中的数字都不重复。

据说“数独”游戏在日本非常流行，在地铁车厢和候车室里，每天都可以看到人们埋头于游戏的情景，甚至有专门的“数独”游戏机出现。

现在很多杂志和报纸上的游戏专版也有数独栏目，一般的方式是提供一个不完整的数独，让读者填完所有数字。

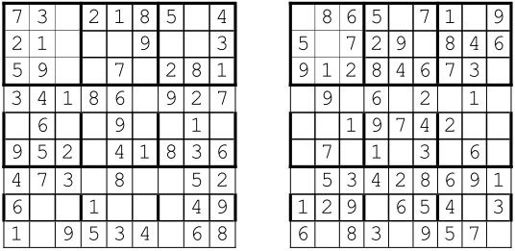
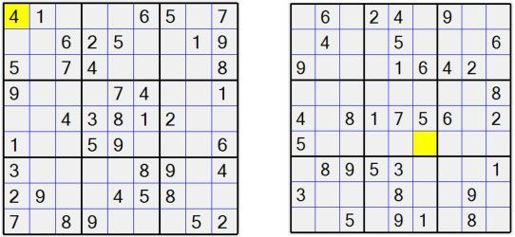
既然数独这个游戏这么好玩，我们也写一个吧！图1-19是作者写的一个数独游戏的初始画面：

图1-19

在面试中，由于时间的限制，面试者不会期望应聘者会写出全部程序，一般会要求回答设计中的几个关键问题，例如：

程序的大致框架是什么？用什么样的数据结构存储数独游戏中的各种元素？如何生成一个初始局面？

分析与解法

看到数独游戏，大家应该都会想到用一个二维的数组来存储，每个元素对应数独中的一个数。但考虑到每一个格子又具有若干个属性（是否可以修改等），我们可以把每一个格子抽象为一个对象，可以把整体看成9×9的格子对象。为什么不使用9个3×3的形式来存储呢？这主要取决于，数据结构是否方便我们去计算游戏的规则（每行每列的每个3×3块都刚好含有数字1～9各一个）。

确定数据结构后，我们的任务就是要生成一个游戏的初始局面。如果随机地把1～9的数字散布在9×9的格子上，这看起来也是可以的，但我们不能保证这个初始局面有解，粗略计算一下，随机生成的数字能满足数独条件的几率还是很低的，大约远远小于10^－20，估计这样的程序运行几天也不一定能产生一个合法的数独！反过来想一下，我们可以先生成一个完整而合法的解，然后再随机去掉一些格子中的数字，这样比较可行。

【解法一】

假设，我们使用下面的结构来存储数独游戏：

下面的GenarateValidMatrix()函数用经典的深度优先搜索来生成一个可行解。我们从（0，0）开始，对于没有处理过的格子，首先调用GetValidValueList(coCurrent)来获得当前格子可能的取值选择，并从中取一个为当前格子的取值，接着搜索下一个格子。在搜索过程中，若出现某个格子没有可行的取值，则回溯，修改前一个格子的取值。直到所有的格子都找到可行的取值为止，这个时候我们就找到了一个可行解。

代码清单1-23

一个可行解生成之后，我们可以随机删去一些格子中的数值。我们删除的数字越少，游戏就越简单；删除的数字越多，游戏就越难，而且可能有多种解法，但是这也没有什么关系——我们判断一个游戏是否结束，不是根据用户填写的数字是否等于我们原来生成的数据，而是根据：

（a）所有的格子都填完；

（b）所有的行、列、小矩阵都符合条件。

【解法二】

上面提到的解法虽然经典，但是并不是唯一的正解，还有许多别的解法。例如，假设已经有一个3×3的矩阵是排列好了的，具体数字姑且用字母代替，如图1-20所示：

图1-20

把整个数独矩阵的各个小矩阵分别命名为B₁，B₂，…，B₉，如图1-21所示：

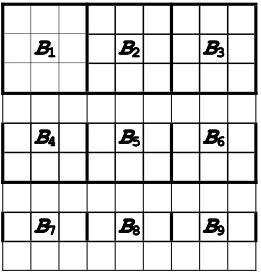
图1-21

那么，可以把这个矩阵放在数独的中央（B₅）的位置上，然后看看有没有一种办法能“生成”其他格子内的合法排列，如图1-22所示：

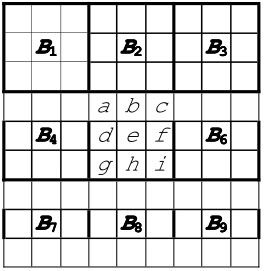
图1-22

第一步，先通过置换行的办法，把B₄和B₆矩阵填好，可以看出abc这一行被移到了另外两个矩阵中不相同的行上。def、ghi这两行也一样，如图1-23所示。

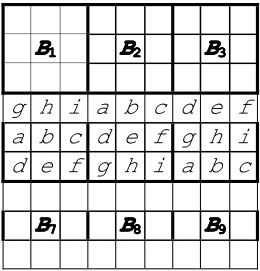
图1-23

第二步，对中央小矩阵的每一列做同样的变换，把B₂和B₈都解决了，如图1-24所示。

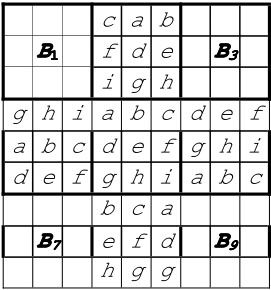
图1-24

第三步，对4个角上的小矩阵，能通过对其相邻矩阵进行类似置换得到么？试试看，通过列置换的方式，用B₄生成B₁和B₇，用B₆生成B₃和B₉，如图1-25所示。

图1-25

看起来这整个数独矩阵是合乎规定的！

这么说，可以用{1，2，3，4，5，6，7，8，9}随机映射到{a，b，c，d，e，f，g，h，i}上，这样会生成9！个不同的数独。需要说明的是，这并不包括所有合法的数独，差得很远^⑭。但是对于一般玩数独的游戏爱好者来说，已经足够他们玩一阵的了。还可以通过部分行或列的局部对换来增加变化的数目。这种办法的优点是程序非常简单，简单到不值得印在纸上。

扩展问题

在应用程序中，有很多大大小小的窗口／按钮／控件。我们经常要判断鼠标点击的位置是不是在某一个窗口／按钮／控件上，或者某个控件跟某个窗口的关系（该控件是否在窗口中，是否跟窗口相交等）。而这些窗口／按钮／控件，可以把它们抽象为一个跟屏幕的长宽平行的大小不同的矩形。为了方便地完成上面这些经常性的操作，应该如何表示这些窗口？

附：下面是笔者用程序生成的几个数独游戏，难度由浅入深，读者不妨一试：