1.4　买书问题

在节假日的时候，书店一般都会做促销活动。由于《哈利波特》系列相当畅销，店长决定通过促销活动来回馈读者。在销售的《哈利波特》平装本系列中，一共有五卷，用编号0，1，2，3，4来表示。假设每一卷单独销售均需要8欧元^⑦。如果读者一次购买不同的两卷，就可以扣除5％的费用，三卷则更多。假设具体折扣的情况如下：

在一份订单中，根据购买的卷数以及本书，就会出现可以应用不同折扣规则的情况。但是，一本书只会应用一个折扣规则。比如，读者一共买了两本卷一，一本卷二。那么，可以享受到5％的折扣。另外一本卷一则不能享受折扣。如果有多种折扣，希望能够计算出的总额尽可能的低。

要求根据这样的需求，设计出算法，能够计算出读者所购买一批书的最低价格。

分析与解法

怎么购买比较省钱呢？第一个感觉，当然是先优先考虑最大折扣，然后再次之。

这的确是一个有效的办法。那么这个算法是不是最省钱的呢？如果我们要买两本第一卷，两本第二卷，两本第三卷，一本第四卷，一本第五卷。

按照优先考虑最大折扣的策略，我们先买各卷各一本，花去5×8×（1－25％）＝30，再买第一，二，三卷，花去3×8×（1－10％）＝21.6，总共51.6欧元。但是如果我们换一个策略，先买第一、二、三、四卷，然后再买第一、二、三、五卷，那么总共花去2×（4×8×（1－20％）＝51.2欧元。

从上面我们可以发现，这些折扣有一定的规律。在同样是买8本书的情况下，选择分别按照3本和5本，以及按照两个4本的付法，费用会不一样。也就是说，针对这个问题试图用贪心策略行不通。

【解法一】

那么针对这种问题的解法，动态规划是一个不错的选择。那么，不妨试一下动态规划的方法。

首先，在使用动态规划之前，得考虑怎么表达购买中间出现的状态。假设我们用X_n来表示购买第n卷书籍的数量。如果要买X₁本第一卷，X₂本第二卷，X₃本第三卷，X₄本第四卷，X₅本第五卷，那么我们可以用（X₁，X₂，X₃，X₄，X₅）表示我们要买的书，而F（X₁，X₂，X₃，X₄，X₅）表示我们要买这些书需要的最少花费。

如果我们要买X₃本第一卷，X₂本第二卷，X₁本第三卷，X₄本第四卷，X₅本第五卷呢？是否需要用F（X₃，X₂，X₁，X₄，X₅）来表示呢？其实不难看出，因为各卷的价格一样，需要的最少花费仍然等于F（X₁，X₂，X₃，X₄，X₅）。也就是说，F（X₁，X₂，X₃，X₄，X₅）等价于F（X₃，X₂，X₁，X₄，X₅）。因此我们没有必要区分不同的卷。那么对于所有跟（X₁，X₂，X₃，X₄，X₅）等价的情况，我们用什么来表示呢？F（X₁，X₂，X₃，X₄，X₅）还是F（X₁，X₂，X₃，X₅，X₄）？还是……

根据排列组合的规则，最多有5！种可选择的表示方法，我们可以选择一种特别的表示（Y₁，Y₂，Y₃，Y₄，Y₅）（其中，Y_n用来表示购买第n卷书籍的数量，Y₁，Y₂，Y₃，Y₄，Y₅是X₁，X₂，X₃，X₄，X₅的重新排列，满足Y₁＞＝Y₂＞＝Y₃＞＝Y₄＞＝Y₅），我们称它为所有跟（X₁，X₂，X₃，X₄，X₅）等价的情况的“最小表示”。

接下来，就需要考虑怎么把一个大问题转化为小一点的问题。

假定要买的书为（Y₁，Y₂，Y₃，Y₄，Y₅）。如果第一次考虑为5本不同卷付钱（当然这里需要保证Y₅＞=1），那么剩下还要再付钱的书集合为（Y₁－1，Y₂－1，Y₃－1，Y₄－1，Y₅－1）。如果第一次考虑买4本不同卷（Y₄＞=1），那么我们接下来还需要买的书集合为（Y₁－1，Y₂－1，Y₃－1，Y₄－1，Y₅）。

根据题意，只要是不同卷的书组合起来就能享受折扣，至于具体是哪几卷，并不要求。因此，就可以不用考虑其他可能比如（Y₁－1，Y₂－1，Y₃－1，Y₄，Y₅－1）。

其他同理，根据如上的推理可以得到状态转移方程：

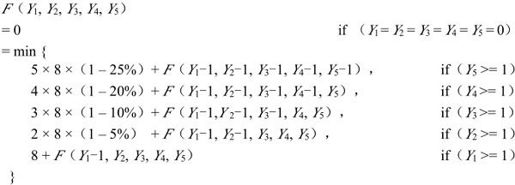
状态转化之后得到的（Y₁－1，Y₂－1，Y₃－1，Y₄－1，Y₅）等可能不是“最小表示”，我们需要把它们转化为对应的最小表示。比如：

从上面的表示公式中可以看出，整个动态规划的算法需要耗费O（Y₁×Y₂×Y₃×Y₄×Y₅）的空间来保存状态的值，所需要的时间复杂度也为O（Y₁×Y₂×Y₃×Y₄×Y₅）。

【解法二】

对于上面的算法，时间复杂度仍然很大。那么，对于这个问题还有没有别的办法呢？贪心策略是否有办法成功呢？

该贪心策略会在买5＋3本的时候出错。因为

5×8×（1－25％）＋3×8×（1－10％）＞4×8×（1－20％）＋4×8×（1－20％）。实际上就是说，在购买8本书的情况下：5×25％＋3×10％＜8×20％。

回过头对比一下：

在小于5本的情况下，直接按折扣买就好了：

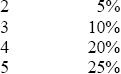
那么如果大于5本呢。

首先，对于大于5本的情况，我们不应该考虑按一本付钱的情况，因为没有折扣。

注明：上面的分解并不适用于所有情况。我们仅考虑的是理论上可能的最大分法，对于不能进行分解的情况，比如购买6本卷一，没有办法享受折扣，因此其折扣将小于上述的讨论情况。同样地，对于购买5本卷一，1本卷二的情况，最多只能享受一种折扣，其折扣也会小于上述的分解情况。对于以下的分解情况，同样适用。

由于折扣的规则仅针对2到5本的情况。对于大于10本的情况，我们可以提出如下的一个假设：

假设在分解的过程中，可以找到如下的一种分法：可以把10本以上的书籍分成小于10的多组（X₁₁，X₁₂，X₁₃，X₁₄，X₁₅），（X₂₁，X₂₂，X₂₃，X₂₄，X₂₅）…（X_n1，X_n2，X_n3，X_n4，X_n5），并且使得只要把每组的最优解相加，就可以得到全局的最优解。

那么，对于大于10的情况，都可以分解为小于10的情况。

假设这样的分法存在，那么就可以按照小于10的情况考虑求解。如果要买的书为（Y₁，Y₂，Y₃，Y₄，Y₅）（其中Y₁＞＝Y₂＞＝Y₃＞＝Y₄＞＝Y₅），贪心策略建议我们买Y₅本五卷的，Y₄－Y₅本四卷，Y₃－Y₄本三卷，Y₂－Y₃本两卷和Y₁－Y₂本一卷。由于贪心策略的反例，我们把K本五卷和K本三卷重新组合成2×K本四卷（K＝min{Y5，Y3－Y4}）。结果就是我们买Y5－K本五卷的，Y₄－Y₅本四卷，Y₃－Y₄－K本三卷，Y₂－Y₃本两卷和Y₁－Y₂本一卷（K＝min{Y₅，Y₃－Y₄}）。比如我们要买3本第一卷，2本第二卷，6本第三卷，1本第四卷和7本第五卷，像前面所说的，我们要买的书可以用（7，6，3，2，1）表示。新的经过调整的贪心策略告诉我们应该买三本四卷，三本两卷和一本一卷。

那么这种分法是正确的吗？有办法证明或者找到反例吗？读者可以直接和我们联系。