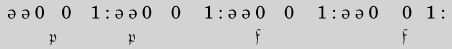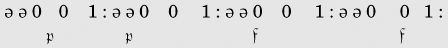毫无疑问,图灵意识到了,在一篇数学论文中介绍一台想象中的计算机器,这种做法既新颖又大胆。就像一位优秀的数学家所做的那样,他给出了这些机器的定义和形式化的描述。他并不需要给出什么例子,但我猜测,他也知道读者们必定不会仅仅满足于抽象的内容,他们需要实实在在的东西。他现在就来满足大家的这一期望。
3. Examples of computing machines.
I. A machine can be constructed to compute the sequence 010101….
3. 计算机器示例
Ⅰ. 可以构造一台计算序列010101…的机器。
这台机器打印出来的纸带会是这样:

但也不完全是这样。就像图灵后面要解释的,他更希望他的机器只使用相间的方格来打印数字序列。第一台样机实际上打在纸带上的是这样:

图灵使用了德国哥特式字体的小写字母表示机器的m-格局。这些字母需要花点时间来适应,因此我会注意指出一些可能会带来麻烦的字母。图灵在他的第一台样机中使用的字母是b、c、k和e。(注意:德文的k看起来像f。)
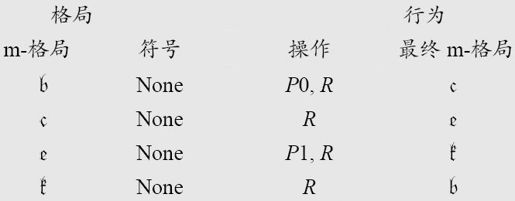
The machine is to have the four m-configurationsand is capable of printing “0” and “1”. The behaviour of the machine is described in the following table in which “R” means “the machine moves so that it scans the square immediately on the right of the one it was scanning previously”. Similarly for “L”. “E” means “the scanned symbol is erased” and “P” stands for “prints”.
这台机器有四种m-格局:并且可以打印0和1。下表描述了机器的行为,其中“R”指“移动机器使其扫描紧跟在刚才扫描的方格右边的那个方格”。类似的,“L”就指移动到左边一格,“E”表示“擦除扫描符”,“P”指“打印”。
在表中,P后面总是跟着要打印的字符。例如,P0指打印一个0,P1指打印一个1,而Px则表示打印一个x。
This table (and all succeeding tables of the same kind) is to be understood to mean that for a configuration described in the first two columns the operations in the third column are carried out successively, and the machine then goes over into the m-configuration described in the last column.
可以这样理解这个表(以及接下来所有这类表):对于前两列中描述的格局,第三列的操作会被陆续执行。然后机器会转到最后一列的m-格局。
表有四列,分为两对

机器的行为取决格局,也就是m-格局和被扫描方格中的符号。第三列包含了各项操作(只能是P、E、L和R)。第四列则是下一个m-格局。
通常,第二列明确表示了一个特定的扫描符,如0或1,但是图灵也使用了“Any”这个词表示任何符号,也使用了“None”一词表示没有符号,也就是一个空白的方格。(对现在的程序员来说,这可能有点让人困惑,因为现在程序员已经习惯于将空格视为与其他字符一样的符号了。而当图灵使用“Any”时,他通常意指“任何非空格”的符号。)对于任何符号包括空格在内的情况,我们这样处理:
When the second column is left blank, it is understood that the behaviour of the third and fourth columns applies for any symbol and for no symbol.
如果第二列留空,则理解为第三列和第四列的行为适用于任何符号以及没有符号的情形。
幸运的是,引发歧义的可能性非常小。
The machine starts in the m-configurationwith a blank tape.
机器装上一条空白纸带后,从m-格局开始运行。
图灵的机器总是以m-格局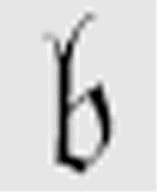 (意为begin,或者更恰当地,
(意为begin,或者更恰当地,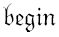 )开始。下面便是我们期待已久的机器。
)开始。下面便是我们期待已久的机器。
可以像这样读这些行:对于m-格局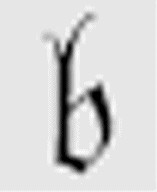 ,当扫描格为空(符号“None”)时,打印0,将读写头向右移动一格,然后转换到m-格局
,当扫描格为空(符号“None”)时,打印0,将读写头向右移动一格,然后转换到m-格局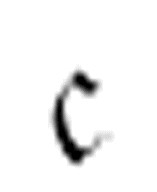 。
。
让我们启动这台机器,观察一下它是如何工作的。我们以m-格局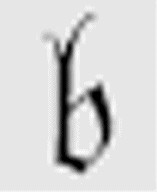 和一条空白纸带开始。尽管理论上纸带两头都是无限延伸的,但是图灵这篇论文中描述的机器只需要纸带无限向右延伸即可,可计算序列中的数字就打在这些地方。
和一条空白纸带开始。尽管理论上纸带两头都是无限延伸的,但是图灵这篇论文中描述的机器只需要纸带无限向右延伸即可,可计算序列中的数字就打在这些地方。

读写头可以用很多种记号来表示。我这里选择了一个围绕当前被扫描方格的粗边框。初始时可以把读写头放置在纸带的任意位置:

扫描格里面没有符号。上表告诉我们,对于m-格局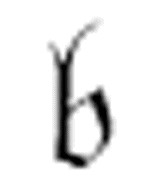 ,如果没有符号,则机器打印0,然后右移一格。
,如果没有符号,则机器打印0,然后右移一格。

新的m-格局是 。如果方格为空,右移一格,转到m-格局
。如果方格为空,右移一格,转到m-格局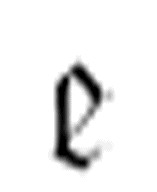 :
:

对于m-格局 ,如果方格里没有符号,打印1,然后右移:
,如果方格里没有符号,打印1,然后右移:

现在我们来到了m-格局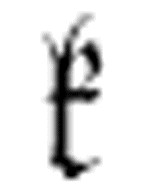 。右移:
。右移:

机器现在到达了m-格局 ,回到了初始状态,并重新开始这样的循环。机器将以这样的方式打印一个由0和1组成的无限序列。
,回到了初始状态,并重新开始这样的循环。机器将以这样的方式打印一个由0和1组成的无限序列。
把表中四行的每一行都视为一个指令,这听上去很诱人,而且事实上,图灵后来也采用了这个术语。但是,我们要认识到这些行并不是给机器的指令,它们只是对机器的描述。这就是为什么采用“状态”这一术语更好的原因。如果我们认为这些行是指令,那也就是在暗示我们可以用其他指令来代替它们,从而让同一台机器表现出不同的行为,但那就意味着机器是在解释那些指令,而事实并不是这样(至少现在还不是)。这个机器只执行一个特定的任务。机器真正的工作原理并不重要,重要的是我们可以使用基于格局、符号和操作这些术语的标准方式来表示机器的工作情况。
这台机器能选出来吗?这种特定的机器可以用多种不同的方式制造出来。它可能有一个转轮,转轮的圆周上是一个能交替打印0和1的自动回墨型橡皮印章。创造一台完全按上述方式工作的图灵机——一台真的要去扫描并解读字符的机器——需要的内部逻辑结构恐怕比其外部所展示出来的要复杂得多。图灵机最常见的“制造”方式,则是用计算机来模拟。
图灵机根据扫描符在m-格局之间跳转。这种“条件分支”(计算机科学中很常见)并不是这个时代中的早期计算机所擅长的。康拉德·楚泽利用在35毫米胶片上打孔的方式来编码他的机器指令。在他的第一台机器Z1中,所有的指令必须按顺序执行;Z3可以实现跳转,但是条件分支显得非常笨拙。直到计算机开始在内存中存储程序(“储存程序型计算机”),条件分支才变得简单而常规。
在前面那个表中,符号一列总是“None”,意思是只有方格为空时格局才起作用。如果这台机器碰巧扫描到一个有符号的方格,机器将不知所措。它可能会停住,可能会崩溃,也可能会烧掉,还可能会重新格式化硬盘驱动器。我们不知道会发生什么。不过,无论发生什么,这样的机器将不再被认为是“非循环的”。然而,只要这台机器以一条空白纸带开始,那就不是问题。
图灵通过定义一台可以打印序列
01010101…
的机器,来说明这是一个可计算序列。在这个序列前加一个点可将其转换成一个可计算数:
.01010101…
现在我们就知道了,机器正在计算的是有理数1/3的二进制等价形式。如果你把它们的顺序调换一下(先是1再是0),那么机器将计算下面的二进制数
.10101010…
这实际上是2/3。
下面我所展示的机器将计算1/4,其二进制形式为:
.01000000…
这台机器遵循图灵的约定,使用德文字体b、c、d、e和f来表示m-格局:
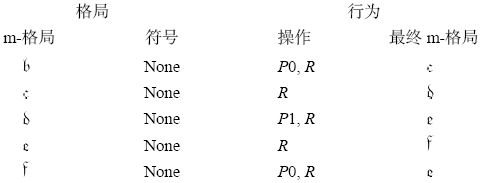
特别注意最后两个m-格局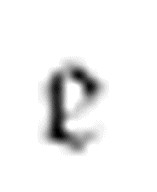 和
和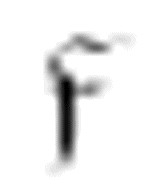 。它们反复交替,便能让机器打印无限的0。机器必须要不断地打印0,才能符合图灵对于“非循环”的定义。
。它们反复交替,便能让机器打印无限的0。机器必须要不断地打印0,才能符合图灵对于“非循环”的定义。
现在应该非常非常明显,我们可以定义类似的计算机器来计算任何有理数。此处,有理数完全不用考虑。
图灵在之前(第1节的第二段)说:“机器也可以改变正被扫描的方格,但只能移到左边或右边一格。”现在,他想要把这条规定变得稍微灵活点。
[234]
If (contrary to the description in §1) we allow the letters L, R to appear more than once in the operations column we can simplify the table considerably.
如果(与§1中描述的不同)我们允许字母L、R在操作列中多次出现,那么我们可以大大地简化表格。
(很快,图灵也将允许在一个格局中出现多个P操作。)现在,表中只有一个m-格局,所有的操作都依赖于扫描符。如果扫描符为None(只有当机器开始运行时出现),那么机器仅仅打印一个0。

读写头不移动。机器的m-格局仍保持不变,但现在扫描符为0,于是机器就向右移动两格然后打印1:

现在扫描符为1,那么机器向右移动两格然后打印0:

又一次,机器在相间的方格中打印0和1了。
这里,我们有一个重要的收获:任何一个特定的序列都可以由各种不同的机器计算出来。不过,某个以空白纸带开始的自动机总是计算出相同的序列。(当然,我这里指的是自动机,因为选择机允许人为操作干涉,这样就可以创造出不同的序列。图灵在论文中几乎没有考虑选择机。)向图灵的自动机中插入任何不确定的或者随机的因素,或者获得来自“外部世界”的信息(比如时间和日期、经度和纬度、或者一个网页),都是不可能的。
在一个格局中使用多个L、R和P操作可以大大简化机器,但要牢记的是,这些简化的表总是可以转化到之前那个严格的每个状态只允许有一个操作的表。现在看来这仅仅是一个不足为谈差别,但之后它就会变得非常重要。
II. As a slightly more difficult example we can construct a machine to compute the sequence 001011011101111011111…
Ⅱ. 再举个稍微困难点的例子:构造一台机器来计算序列001011011101111011111…
“稍微”困难点?注意图灵现在想要做的是什么。这个序列里包含了越来越长的连续的1,它们之间由0相隔。开始时是一个1,之后是两个1,然后三个1,等等。图灵明显已经厌倦计算有理数了,现在他想处理的是一个无理数,很可能还是一个超越数。
当这台新机器打印连续的1时,它必须用某种办法“记住”之前一轮中打印了多少个1,然后在这一轮多打印一个。通过来回扫描,这台机器总能访问前一轮的内容,从而能够利用这一信息打印下一轮。图灵究竟是如何做到这一点的,研究起来会非常有意思。
图灵又一次使用德文字体中的小写字母来表示m-格局,这次的字母是o、q、p、f和b。
The machine is to be capable of five m-configurations, viz.and of printing “ә”, “x” “0” “1”. The first three symbols on the tape will be “әә0”; the other figures follow on alternate squares.
这台机器具备5个m-格局,即和
, 并能打印“ә”,“x”,“0”,“1”。纸带上的最前面三个符号会是“әә0”,其他数字在后面相间的方格中出现。
这是图灵首次提到在相间的方格中打印数字(0、1,或者其他第一类符号)。假设最左边的符号出现在纸带的左端,则他想要纸带最后变成:

当然,纸带永远不会在“最后”变成什么,因为机器会永远运转下去。要使它符合“非循环”的要求,它必须永远不停地打印。
在语音学和语言学领域中,字符ә是大家熟悉的中央元音。图灵使用这个中央元音代表程序员们所说的哨兵(sentinel)。在这个例子中,它是一个指明数字边界的特殊字符。只要方格中的扫描符不是中央元音,读写头就一直向左移动,这样机器可以把读写头移到纸带的最开始处。(为什么这里有两个中央元音?这个例子中只需要一个就够了,但是图灵之后构造的机器需要两个中央元音作为哨兵。他在这个例子中加入第二个中央元音可能是为了保证前后一致。)
在第一台样机中,0和1之间的空格是没有用的,而在这个例子里,空格会扮演着非常重要的角色。
On the intermediate squares we never print anything but “x”. These letters serve to “keep the place” for us and are erased when we have finished with them.
在中间的方格中,我们只打印x,不打印别的东西。它们用来帮我们“记位置”,用完之后就被擦除。
图灵将纸带上的方格分为两类。机器在每隔一格的地方打印0和1。除了“哨兵”字符,这些方格中没有其他的符号。图灵把中间夹着的方格作为某种临时便笺使用。因此,我们现在可以将其分别称为“数字格”(包含0和1)和“非数字格”(包含其他的字符)。(图灵后来把他们称为F格和E格,分别代表figures和erasable。)
We also arrange that in the sequence of figures on alternate squares there shall be no blanks.
我们还要求,相间方格里的数字序列中没有空格。
机器逐步算出0和1的同时,也把它们从左到右顺次打印出来。机器计算出来的每个新数字都被打印到下一个可用的空的数字格中,不会跳过任何数字格。这些限制构成了一整套规则(有些明显表述出来了,有些则是暗示出来的),后来被埃米尔·波斯特称作“图灵规范机器”。[1]这比一般的“图灵机”约束更多。图灵规范机器从不擦除数字格,也不在一个已有数字的数字格上覆盖一个不同的数字。在后文中,这些隐含的规则将变得非常重要。
下面是图灵的格局表,用来计算他定义的无理数。
和前面一样,机器以m-格局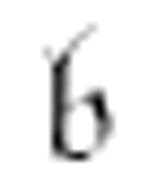 开始。它首先打印两个中央元音和两个0。纸带将变成:
开始。它首先打印两个中央元音和两个0。纸带将变成:

m-格局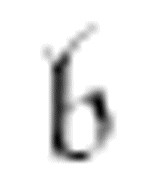 执行的是程序员称为初始化的任务,此后机器再也不会进入m-格局
执行的是程序员称为初始化的任务,此后机器再也不会进入m-格局 。
。
在我们翻看机器内部弄得满手是油之前,先来大致体会一下其他m-格局是干什么的。在一些格局(特别是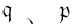 和
和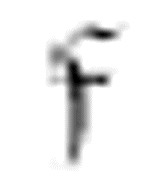 )中,操作列展示了一次移动两格的情况:R,R或者L,L。在这些情况下,机器能够有效地沿着数字格(
)中,操作列展示了一次移动两格的情况:R,R或者L,L。在这些情况下,机器能够有效地沿着数字格( 和
和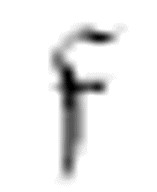 的情况)或非数字格(
的情况)或非数字格( 的情况)移动。
的情况)移动。
除了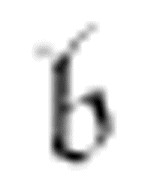 之外,其他m-格局还会在遇到特定的扫描符时转回到自身。程序员通常称这样的操作为循环。循环可以实现重复性的工作,甚至包括寻找某个特定的符号这样简单的操作。
之外,其他m-格局还会在遇到特定的扫描符时转回到自身。程序员通常称这样的操作为循环。循环可以实现重复性的工作,甚至包括寻找某个特定的符号这样简单的操作。
m-格局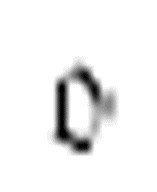 在数字格上穿过一连串的1自右向左移动,机器在这个过程中每发现一个1,就会在这个1的右边打印一个x,然后向左移动检查下一个数字格。结束时,它将转换到m-格局
在数字格上穿过一连串的1自右向左移动,机器在这个过程中每发现一个1,就会在这个1的右边打印一个x,然后向左移动检查下一个数字格。结束时,它将转换到m-格局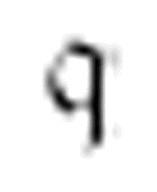 。
。
m-格局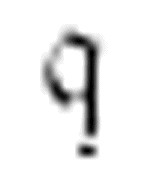 从左至右沿着数字格移动,直到它遇到一个空格。这是当前序列结束的地方。然后它打印一个1,向左移动(至一个非数字格),转到m-格局
从左至右沿着数字格移动,直到它遇到一个空格。这是当前序列结束的地方。然后它打印一个1,向左移动(至一个非数字格),转到m-格局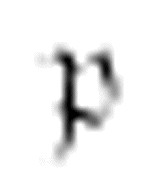 。
。
类似地,m-格局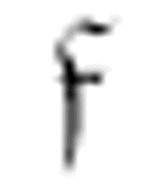 也沿着数字格向右移动,直到遇到一个空格,然后打印一个0,向左移动两格,再转换到m-格局
也沿着数字格向右移动,直到遇到一个空格,然后打印一个0,向左移动两格,再转换到m-格局 。
。
m-格局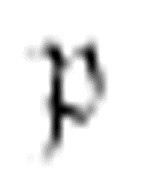 相当于一个调度员。绝大多数时间里,它都是在非数字格上向左移动寻找x符号。当发现一个x,它就将其擦除,向右移动,并转到m-格局
相当于一个调度员。绝大多数时间里,它都是在非数字格上向左移动寻找x符号。当发现一个x,它就将其擦除,向右移动,并转到m-格局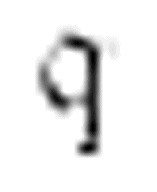 。如果它遇到一个中央元音便向右移动,并且转换到m-格局
。如果它遇到一个中央元音便向右移动,并且转换到m-格局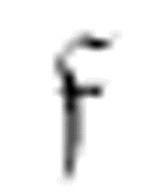 。
。
图灵使用符号x的方式很聪明。当构造一串新的连续数字1时,机器先在前一串连续数字1中的每一个1后打印一个x,随后在已有序列的最后打印一个1,然后每有一个x就再打印一个1,从而让串的长度增加了1。
尽管我们可以在每一个操作之后说明纸带的情况,但是对于这个例子,最好还是在每一个格局结束时查看一下纸带。
机器从m-格局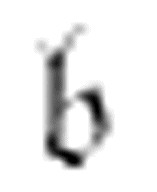 至
至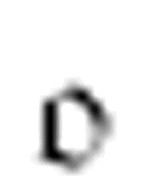 。但是,对于扫描符0,
。但是,对于扫描符0,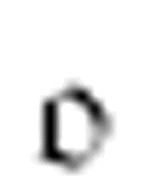 不做任何事,而是直接转到m-格局
不做任何事,而是直接转到m-格局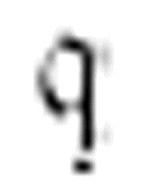 。对于m-格局
。对于m-格局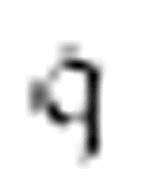 ,如果扫描符是0或1,读写头向右移动两格并仍处于相同的m-格局。但若碰到一个空格,它将在打印一个1后向左移动。总而言之,m-格局
,如果扫描符是0或1,读写头向右移动两格并仍处于相同的m-格局。但若碰到一个空格,它将在打印一个1后向左移动。总而言之,m-格局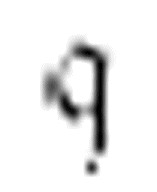 沿着数字格向右移动,直到它遇到一个空格,然后打印一个1,再向左移动。
沿着数字格向右移动,直到它遇到一个空格,然后打印一个1,再向左移动。

下一个m-格局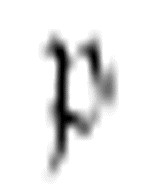 一般沿着非数字格移动。它向左移动两格,直到遇到一个包含x或中央元音的非数字格。在这个例子中,它遇到的是中央元音,于是向右移动:
一般沿着非数字格移动。它向左移动两格,直到遇到一个包含x或中央元音的非数字格。在这个例子中,它遇到的是中央元音,于是向右移动:

m-格局是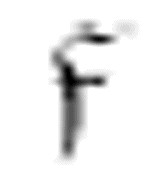 时,读写头沿着数字格移动。它保持每次向右移动两格,直到扫描到空格。这时候它就会打印一个0,然后向左移动两格:
时,读写头沿着数字格移动。它保持每次向右移动两格,直到扫描到空格。这时候它就会打印一个0,然后向左移动两格:

这就是在连续数字1之间打印0的方法。
现在我们来到了m-格局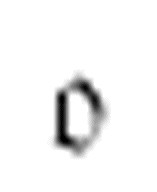 。这个m-格局总是开始于一连串数字1中最右边的那个1。它的任务是在每一个1的后面打印一个x,在这串连续数字1的左侧的0处停止。
。这个m-格局总是开始于一连串数字1中最右边的那个1。它的任务是在每一个1的后面打印一个x,在这串连续数字1的左侧的0处停止。

回到m-格局 。这个m-格局沿着数字格向右移动直到遇到空格,在打印一个1后向左移动。
。这个m-格局沿着数字格向右移动直到遇到空格,在打印一个1后向左移动。

m-格局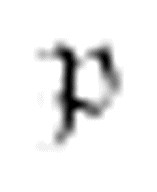 沿着非数字格向左移动,直到遇到一个x或者中央元音。当它遇到一个x,就擦除这个x,并向右移动。
沿着非数字格向左移动,直到遇到一个x或者中央元音。当它遇到一个x,就擦除这个x,并向右移动。

又一次回到m-格局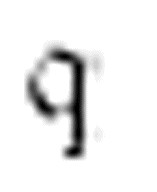 。沿着数字格向右移动,直到碰到一个空格,在打印完一个1后向左移动。
。沿着数字格向右移动,直到碰到一个空格,在打印完一个1后向左移动。

现在我们处于了m-格局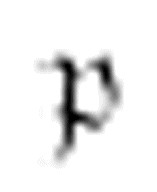 中。沿着非数字格向左移动,直到扫描到中央元音,之后向右移动。
中。沿着非数字格向左移动,直到扫描到中央元音,之后向右移动。

m-格局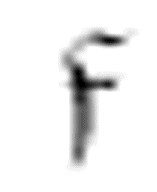 在数字格上向右移动,直到它遇到一个空格,它打印完一个0后向左移动两格。
在数字格上向右移动,直到它遇到一个空格,它打印完一个0后向左移动两格。

这样看起来确实奏效。我们现在有了连续的一个1和连续的两个1,我们来看一下它能否继续按我们的期望工作下去。
m-格局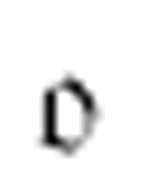 的工作是在最后那串连续数字1的每一个1后打印一个x。
的工作是在最后那串连续数字1的每一个1后打印一个x。

m-格局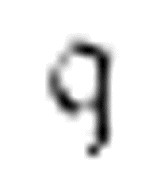 沿着数字格向右移动,直到遇到一个空格。然后,它打印一个1,向左移动。
沿着数字格向右移动,直到遇到一个空格。然后,它打印一个1,向左移动。

注意,现在这里有两个x,并且现在这串连续数字1还差两个1。对于每一个要被擦除的x,都会有一个1打印出来。m-格局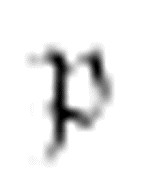 沿着非数字格向左移动,直到遇到一个x,然后擦除x并向右移动。
沿着非数字格向左移动,直到遇到一个x,然后擦除x并向右移动。

m-格局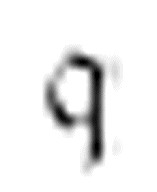 沿着数字格向右移动,直到遇到一个空格,打印一个1后向左移动。
沿着数字格向右移动,直到遇到一个空格,打印一个1后向左移动。

回到m-格局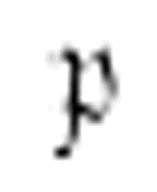 ,继续向左移动,直到遇到x,擦除x后向右移动。
,继续向左移动,直到遇到x,擦除x后向右移动。

m-格局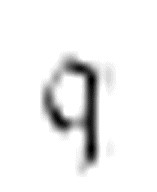 在结尾处再打印一个1。
在结尾处再打印一个1。

现在是m-格局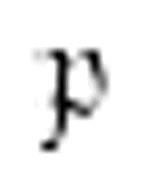 ,读写头向左移动,直到遇到一个中央元音。
,读写头向左移动,直到遇到一个中央元音。

m-格局 沿着数字格向右移动,直到序列的末端,打印一个0。
沿着数字格向右移动,直到序列的末端,打印一个0。

现在机器已经成功地打印了包含三个1的连续数字串和一个0。
图灵是如何想到这台机器所使用的技巧的呢?我猜他抵住了直接去数的诱惑,而是尝试手动计算这个序列。他可能发现了,可以通过在数字上标注小标记来追踪连续的数字串。这些小标记变成了机器打印在非数字格中的字符x。
纸带的示意图并没有出现在图灵的论文中,他没有兴趣为机器或其操作提供这种赤裸的“写实”图示。相反,他有一种别的方法来表示机器的工作状态。
在其论文的第二部分(本书第67页),图灵说:“在机器运转中的任何阶段,被扫描方格的标号、纸带上所有符号构成的序列以及m-格局,共同描述了这个阶段的完全格局。” 尽管图灵提到的“被扫描方格的标号”有点怪,因为方格并没有明确的编号,不过对于只在一个方向无限延伸的纸带,方格有隐含的编号。
图灵将要展示一种用完全格局——即纸带的快照加上当前m-格局和扫描格——来表示机器工作状态的方法。
To illustrate the working of this machine a table is given below of the first few complete configurations. These complete configurations are described by writing down the sequence of symbols which are on the tape, [235]
with the m-configuration written below the scanned symbol. The successive complete configurations are separated by colons.
为了说明机器的运作,我们给出下表,表中包括了最初的几个完全格局。我们写下纸带上的符号序列,并把m-格局写在扫描符下面,以此来描述这些完全格局。后续的完全格局用冒号隔开。
在论文中,接下来是一个“表”的四个条目。每个条目各有两行,初看起来非常令人费解。下面是第一个条目。
注意这些冒号!每一对冒号之间的是纸带的连续快照。一些0和0以及(后面)0和1之间的空隙比正常的空格要大一点。这种偏大的空隙代表一个空格。与显示在纸带下的m-格局一起,它们构成了机器的前六个完全格局,显示了目前已经打印在纸带上的所有符号。
第一个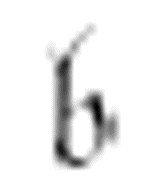 表明起始格局。开始时,纸带是空白的。这个格局打印出了最初两个冒号间的序列,和前面显示的一样:
表明起始格局。开始时,纸带是空白的。这个格局打印出了最初两个冒号间的序列,和前面显示的一样:

之前使用黑框来表示读写头的位置在下一个扫描符处,现在图灵在下一个扫描符的下面给出了下一个m-格局:

因为当扫描符是0时,m-格局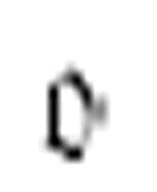 不做任何操作,所以下一个纸带的快照和之前的一样,但是m-格局已经转换成了
不做任何操作,所以下一个纸带的快照和之前的一样,但是m-格局已经转换成了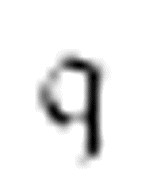 :
:
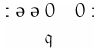
当m-格局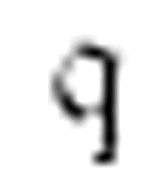 扫描到一个0时,读写头向右移动两格,下一个m-格局仍然是
扫描到一个0时,读写头向右移动两格,下一个m-格局仍然是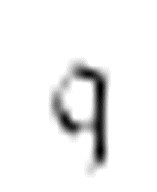 :
:
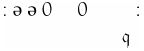
这次的扫描符又是0。读写头向右移动两格, m-格局仍然是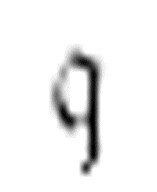 :
:
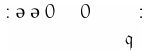
注意,当读写头超过上次打印的字符后,纸带是如何变得更宽点的。现在,扫描符是空格,因此机器打印一个1,向左移动一格,转换到格局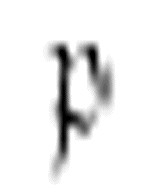 :
:
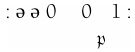
虽然这样做的视觉满足感不及真实的纸带,但是图灵的方法提供了更多的信息,特别是在读写头的当前位置下面指明了下一个m-格局。这些连续的完全格局展现了机器操作的全部历史记录。我们很容易查看其中任何一个完全格局,将m-格局和扫描符与机器的状态匹配起来,最终得到下一个完全格局。
图灵给出的下一个序列展示了m-格局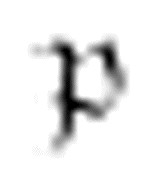 往回搜索,直到找到中央元音,然后转换到格局
往回搜索,直到找到中央元音,然后转换到格局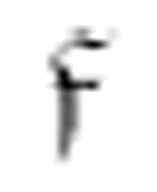 ,转而向右寻找空格。
,转而向右寻找空格。
下一个条目:仍然是m-格局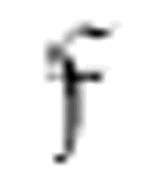 ,机器找到一个空的数字格(注意冒号之间的空间是如何再次加宽的),打印一个0,向左移动两格后转换到格局
,机器找到一个空的数字格(注意冒号之间的空间是如何再次加宽的),打印一个0,向左移动两格后转换到格局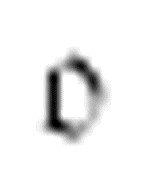 。
。
m-格局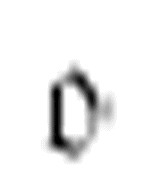 再遇到扫描字符1后向右移动,打印一个x后向左移动三格。
再遇到扫描字符1后向右移动,打印一个x后向左移动三格。
图灵就展示了这么多。如果你觉得这种纸带操作的表示法并不简洁明了,图灵也给出了另外一种方法。
This table could also be written in the form
in which a space has been made on the left of the scanned symbol and the m-configuration written in this space.
这个表也可以写成
在这里,扫描符的左侧留出了一块空隙,m-格局被写在这个空隙里。
图灵使用字母C(代表Configuration,格局)来标识这种格式,他将在第6节中提到。之前展示的完全格局:
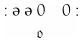
现在可以表示为:

现在,我们可以看出图灵使用德文字体表示m-格局至少有一个原因:以这种格式,m-格局可能没那么容易与机器打印出的符号区别开了。在每一对冒号之间的字符序列将不再同纸带上一模一样,因为需要为下一个m-格局预留一个空格。图灵也承认它有点奇怪。
This form is less easy to follow, but we shall make use of it later for theoretical purposes.
这个形式比较难明白,但出于理论目的,我们后面会用到它。
事实上,使用这种形式是必需的,不过我们还会对此形式再做一下修改。图灵已经着手组装,开始准备后面的一个主要成果展示了:他将展示一个通用计算机器——现在通常称图灵机或者UTM(Universal Turing Machine)——功能上(抛开商业意义不算)等价于现代计算机。
注意最后这个格式的优点:机器的整个操作都被排成一个字符流,这是程序员非常喜爱的形式。当读写文件或者进行数字通信时,理想的方法是读或写字符流,从头到尾一个接着一个,从不向前或向后跳跃。
我们同样注意到,图灵将下一个m-格局移到了下一个扫描符的前面。图灵将这两项合起来定义为格局,并且这两项在完全格局中出现的顺序,与它们在机器表前两列中出现的顺序一致。你可以把这个m-格局和符号配成一对,并通过扫描机器表的m-格局和符号列来寻找匹配项。(很明显,当机器表中的符号列包含的是实际的字符,而不是“Any”、“None”或空白时,这样的查找更简单。)实际上,图灵会在构造他的通用机时让这个搜索过程实现自动化。
图灵接下来讨论了他选择在相间的方格打印数字序列的理由。
The convention of writing the figures only on alternate squares is very useful: I shall always make use of it. I shall call the one sequence of alternate squares F-squares and the other sequence E-squares. The symbols on E-squares will be liable to erasure. The symbols on F-squares form a continuous sequence. There are no blanks until the end is reached.
将数字只写在相间的方格中,这个约定会非常有用,我会一直用到它。我会将其中一个由相间的方格组成的序列称为F-格,另一个这样的序列称为E-格。E-格中的符号可以擦除。F-格中的符号形成一个连续的序列。在到达纸带末端之前,将不会出现空格。
之前我提及这些格时,称它们是数字格和非数字格。只需要记住figures(数字,即0和1)和erasable(可擦除的)这两个单词,你就能分清它们分别是哪个了。“在到达纸带末端之前,将不会出现空格”,这句话只针对F-格。一个可计算序列的数字总是从左至右按次序打印的,从不跳过一个F-格,也不改写F-格中的数字。这些是图灵的通用机所必须遵守的规则。
E-格是一种便笺式存储器,某种程度上可能等价于人类的记忆。
There is no deed to have more than one E-square between each pair of F-squares: an apparent need of more E-squares can be satisfied by having a sufficiently rich variety of symbols capable of being printed of E-squares.
在每对F-格的中间只需要一个E-格:明显需要多个E-格时,可以允许在E-格中打印足够多样的字符。
图灵的第二台机器采用了一种技巧,即通过在E-格中打印x符号来实现字符识别。这是他经常采用的一般性技巧,因而给这一技巧命了名。
If a symbol β is on an F-square S and a symbol α is on the E-square next on the right of S, then S and β will be said to be marked with α. The process of printing this α will be called marking β (or S) with α.
如果符号β在F-格S中,符号α在紧邻S右侧的E-格中,那么S和β就叫做是用α标记的。打印这个α的过程称为用α来标记β(或S)。
下图中的0(在F-格上)称为用x标记的:
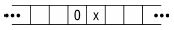
事实说明,这些标记非常方便,这也是图灵最棒的发明之一。
尽管如此,标记并不是强求的。定义一台只使用两个字符的机器,或者只区分空格和被标记格的机器,都是可能的。数学家埃米尔·波斯特在一篇有意思的论文[2]中探讨过这个方法,这篇论文独立地给出了一种设置,它与图灵定义的类似。波斯特设想有一个“工人”和一些“盒子”,这些盒子被排成了一个序列。这个工人能够完成以下工作:
(a) 标记他所在的盒子(假设盒子为空);
(b) 擦除他所在盒子的标记(假设盒子已标记);
(c) 移动到他右侧的盒子里;
(d) 移动到他左侧的盒子里;
(e) 判断他所在的盒子是否被标记。
波斯特其实并没有展示他的工人是如何完成实际应用的。如果方格或者盒子只有被标记和不被标记两种状态,工作起来明显比图灵的捷径费力得多。