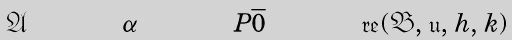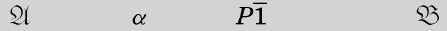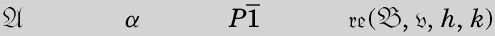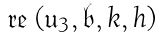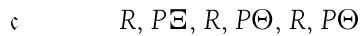we replace by

然后，做进一步的替换。对于以下形式的任何一行

我们将其替换为

被替换的行原来打印0，而不是。格局和，以及扫描符α在此处仅仅是占位符。你可能想到是一个“替换”函数，这里用k替换了纸带上的第一个h，然后转向格局。如果它不能找到一个h，那么转向格局。

正如第4节的定义，函数使用了依赖于中央元音哨兵的函数。这个函数不能调整为用来寻找Θ哨兵的函数。

这就是新机器对原始机器打印每一个数位时的操作方式。当新机器以新数目的F字符开始运作时，纸带上h字符的个数会比F字符的个数多一。因此，机器在转入格局u前会打印h次的，而不是0。

and any line of the form

by

并将以下形式的任何一行

替换为

格局u和需要打印没有上划线的真正的0和1字符，然后为下一数目的F字符准备纸带，并重启机器。图灵将揭示格局和其实是非常相似的。

and we add to the table the following lines:

并且我们在表中增加以下几行：

在格局打印了一个真正的0后，₁打印一个k和两个Θ，对于机器来说这是一个新的哨兵。格局₂和₃用h替换每个k。（在前一轮的调整中，h字符被替换为k。）对于每一个转换为h的k，在其末尾同样会打印一个F。在图灵的表中，存在一个无限的循环，因为₂总是跳转到₃，而₃又总是跳转到₂。替换函数的形式是：

如果没有了可以转换为h的字符k，机器就需要从格局重新开始，格局是原机器的初始格局。格局与之非常相似，除了打印的是1而不是0。

and similar lines with for u and 1 for 0 together with the following line

同样用替代u，1替代0，并加上下面一行：

遗憾的是，这里还存在另一个错误。不应该打印h，应该打印新式的哨兵符：

We then have the table for the machine ′ which computes β. The initial m-configuration is , and the initial scanned symbol is the second ә.

这样我们就为计算β的机器′制定了格局表。初始的m-格局是，初始扫描符是第二个ә。

我们来看看它是否能运作。机器′是的修改版，′主要计算它从纸带上读到的F字符数目的立方根。机器′以有两个中央元音开头的纸带，从格局开始：

格局打印一个和两个Θ。

并没有在任何地方用到。现在机器跳到格局上，两个Θ代替之前的中央元音作为哨兵。这里没有读到F字符，因此计算的是0的立方根。当它需要打印第一个时，它也尝试着将第一个h替换为k。因为没有h字符，所以机器转到格局。这个格局在纸带上打印一个真正的0，后跟一个k和两个Θ：

格局₂和₃组成了一个小循环来将每个k替换为h，并打印一个F：

这里没有可转换为h的k了，因此机器转向格局，并且彻底重新开始计算1的立方根。第一个数字是1，因此机器打印一个，并且把h变为k，就这样持续下去。下一个数字是0，因此它打印一个。这时没有h字符了，因此机器又一次转向格局打印真正的0及一个k和两个Θ。

现在对于每一个k，k都转换为了h，并且紧接着打印一个F：

这里还有一个错误，但我之前并没有修改。F字符需要位于F-格中，因此它们之间需要有空格。不管怎样，已经没有可以转换为h的k字符了，因此机器将会转到格局计算2的立方根。

有了第10节的总结，图灵很满意于他所定义的计算模型，这个模型形式化地包含了所有算法可能需要的东西。现在他已经准备好，要阐述判定性问题无解了。