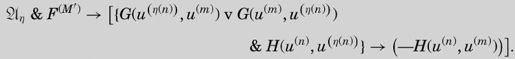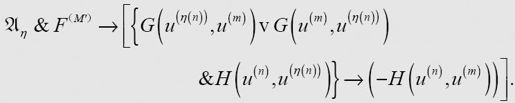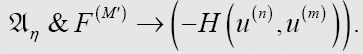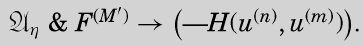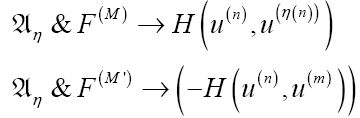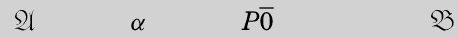and
    and - 图1
    并且
    and - 图2
    第一个蕴涵符的右边是对and - 图3η公理的最后一个表达式的重新描述，只是稍做了调整，以u(n), u(m)和u(η(n))分别代替了w、t和z。将这两个公式合并，
    Hence and - 图4
    The conditions of our second definition of a computable function are therefore satisfied.
    因此 and - 图5
    对于可计算函数的第二个定义的条件也满足了。
    这里的“第二个定义”是指本书第220页以“一种等价的定义是这样的”开始的等价定义。他已经表明，可以创建以下形式的两个命题：
    and - 图6
    对于每一个n和m，其中一个是可证明的。
    Consequently η is a computable function.
    因此，η是一个可计算函数。
    下一个证明包含了论文（及本书）中关于图灵机最后出现的那个表。这台机器将用来证明图灵的定理(iii)。该定理声称，如果ø(m, n)是一个两个整数变量的可计算函数，那么ø(n, n)是n的可计算函数。
    这个证明展示了计算一个定义域为自然数而值域为实数的函数的技巧。对相继的参数（n等于0、1、2等）开始计算这个函数，而当计算完n个数位后，这个函数的计算就停止了。
    Proof of a modified form of (iii).
    Suppose that we are given a machine and - 图7 which, starting with a tape bearing on it әә followed by a sequence of any number of letters “F” on F-squares and in the m-configuration b, will compute a sequence γn depending on the number n of letters “F”.
    对于(iii)变式的证明
    假设给定一个机器and - 图8，该机器初始时的m-格局为b，配备一条以әә开始且在后面的F-格中有任意个字母“F”的纸带，将会根据“F”的个数n来计算序列γn。
    纸带看起来如下：
    and - 图9
    这台机器最有趣的地方在于，它是图灵在这篇文章中提到的与克莱尼和戴维斯描述的重构图灵机的工作方式最接近的一次。这台机器读入纸带上以一类字母“F”编码的非负整数，然后计算此整数的函数。克莱尼和戴维斯的机器执行的是数论函数，但在图灵永远运行机器的精髓里，他隐含地假定γm序列更加复杂——可能是n的立方根。如果机器以读取5个“F”字符开始（像上面展示的纸带中那样），它将会计算5的立方根。
    If øn(n) is the m-th figure of γn then the sequence β whose n-th figure is øn(n) is computable.
    如果øn(m)是γn第m个数字，那么第n个数字为øn的β序列是可计算的。
    例如，函数ø5返回5的立方根的第12个二进制数字。图灵给出了一个新的可计算序列β，对每一个n包含了øn的一个数字。在我举的例子中，β序列的第一个数字是1的立方根的第一个数字，第二个数字是2的立方根的第二个数字，以此类推。
    图灵一开始已经假设了这台机器（无论是一个立方根机还是其他不同的东西）是存在的。接下来他将改造这台机器，通过改变一些现有的指令并增加一些新的指令，来创造一台稍微不同的机器。
    新的机器必须能够以可变数目的F字符运作：一开始没有字符，然后是一个F，两个F字符，等等。在计算了n个（n是字符F的个数加1）数位后，它必须停止计算，然后以一个额外的管理其行为的F字符重新开始。新的机器不会在连续的F-格中打印数字0和1。虽然它们将从左至右按顺序打印，但会淹没在机器的其他输出中。
    图灵希望他的原始机器是一个标准形式，这样修改起来就容易了。
    We suppose that the table fir and - 图10 has been written out in such a way that in each line only one operation appears in the operations column.
    同样假设and - 图11的格局表写成了如下的形式：每一行的操作列中只有一个操作。
    对于这些改动，图灵需要引入一些新的字符，包括希腊大写字母Ξ（读为xi）和Θ（读为theta）。他同时需要替换表中出现的三个字母。
    We also suppose that Ξ, Θ, and - 图12, and and - 图13 do not occur in the table, and we replace ә throughout by Θ, 0 by and - 图14, and 1 by and - 图15.
    同样假设Ξ、Θ、and - 图16和and - 图17都没有出现在表中，并将ə替换为Θ，0替换为and - 图18，1替换为and - 图19。
    当图灵说“将ə替换为Θ”，并不是指在纸带上替换。纸带上仍然需要以两个中央元音哨兵开始。他意指在格局表中，读到ə时就将其改为Θ。
    图灵在这里并没有交代，但机器的修改还要求在机器中并没有用到h和k，且格局 and - 图20对新的定义是适用的。
    Further substitutions are then made. Any line of form
    and - 图21