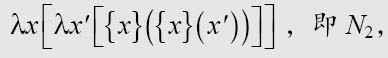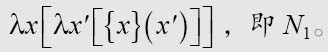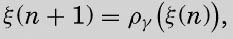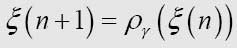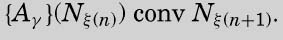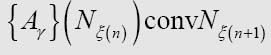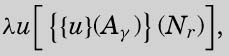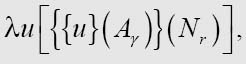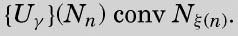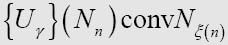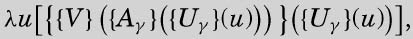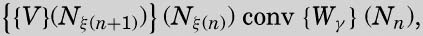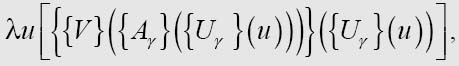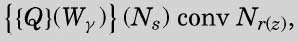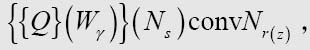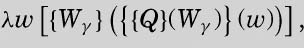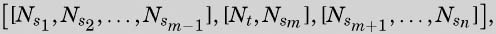and with

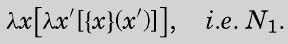
    and with - 图1

    and with - 图22是机器and with - 图3的一部分。提供公式Mγ时，and with - 图4的操作可以划分为很多部分，其中第n部分用来寻找γ的第n位。第n部分的第一阶段是公式{Mγ}(Nn)。这个公式接下来提供给and with - 图52用来将公式连续地转换为其他公式。每一个可转换的公式都会最终出现，并与下列公式进行比较：
    and with - 图6
    及and with - 图7

    这就是数字2和1的冗长的表达式。为了实现一个可以转换λ表达式的机器，你必须在表示法中保持一致，而不包含语法捷径的方法实际上是最简单的。

    If it is identical with the first of these, then the machine prints the figure 1 and the n-th section is finished. If it is identical with the second, then 0 is printed and the section is finished. It it is different from both, then the work of and with - 图82 is resumed. By hypothesis, {Mγ}(Nn) is convertible into one of the formulae N2 or N1; consequently the n-th section will eventually be finished, i.e. the n-th figure of γ will eventually be written down.
    如果与第一个完全一样，那么机器打印1，第n部分完成。如果与第二个相同，那么打印0，这部分也结束了。如果与这两个都不一样，那么and with - 图92的工作就要重新开始。根据假设，{Mγ}(Nn)是可以转换为公式N2或者N1，因此第n部分最终是会结束的，也就是说，γ的第n位最终会写出来。

    在开始更加复杂的变换证明之前，图灵空了一行：如何设计一个能包括特定机器运转情况的λ表达式。

    To prove that every computable sequence γ is λ-definable, we must show how to find a formula Mγ such that, for all integers n,
    and with - 图10
    为了证明每一个可计算序列γ都是λ可定义的，我们必须先说明如何找到一个公式Mγ，对于所有的整数n，
    and with - 图11

    这个公式正好和之前那个一样，只是最后那个N的下标被重排了。现在，要做的不是描述一个操作λ函数的机器，而是定义一个模拟机器的λ函数。

    Let and with - 图12 be a machine which computes γ and let us take some description of the complete configurations of and with - 图13 by means of numbers, e.g. we may take the D.N of the complete configuration as described in §6.
    假设and with - 图14是一台计算γ的机器，我们来用数字描述一下and with - 图15的完全格局。正如§6中描述的，我们可以得到完全格局的描述数。

    在下面的讨论中，我将会引用到“格局数”，这其实就是简单的连续整数0, 1, 2, 3等，这个数字随机器运转而递增。对于任何一个特定的机器，对每个格局数，存在一个与完全格局对应的描述数。这些是非常大的数字，包括了描述纸带上已打印数字及下一个m-格局的代码。

    Let and with - 图16(n) be the D.N of the n-th complete configuration of and with - 图17.
    令and with - 图18(n)为and with - 图19的第n个完全格局的描述数。

    图灵在这里使用的n是我所指的格局数，而and with - 图20(n)是一个描述数。

    The table for the machine and with - 图21 gives us a relation between and with - 图22(n+1) and and with - 图23(n) of the form
    and with - 图24

    where ργ is a function of very restricted, although not usually very simple, form: it is determined by the table for 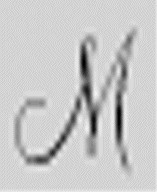and with - 图25.

    从and with - 图26的格局表中，我们可以得到and with - 图27(n+1)及and with - 图28(n)之间的如下关系：
    and with - 图29
    其中ργ是一个严格受限的函数，尽管通常不是很简单：其形式由and with - 图30的格局表决定。

    ργ函数将一个描述数转换为下一个描述数。一般来讲，输入是一个长的数字，输出是另一个长的数字。这个函数基本上必须在这个长输入数中，寻找一组对应于m-格局和扫描符的特定模式的数字，并基于格局表构造下一个完全格局，有可能包含一个新的打印符号，并改变m-格局和下一个扫描符。

    图灵对于这个函数的“通常不是很简单”的描述切中目标。这个函数需要将描述数拆分为单个数位并验证它们。因为描述数是十进制数，所以这个函数可以通过先将数字除以10的幂，忽略分数部分，再除以另一个10的幂，保留余数，来抽取其中任意长度的部分。尽管ργ函数毫无疑问是很复杂的，但它肯定是能被想到的。

    ργ is λ-definable (I omit the proof of this), i.e. there is a W.F.F.Aγ such that, for all integers n,
    and with - 图31
    ργ是λ可定义的（我略去了这部分的证明），即存在一个合式公式Aγ，对于所有的整数n：
    and with - 图32

    Aγ本质上是与ργ一样的函数，只不过是用λ演算的语言表示的。它用来进行描述数间的转换。

    Let U stand for
    and with - 图33
    where r=and with - 图34(0);
    令U表示
    and with - 图35
    其中r=and with - 图36(0);

    这句开头的大写U应该有一个下标γ，因为它是基于一个特定可计算序列的。Nr是机器开始时的完全格局的描述数——数字313。这个数字对应于标准描述DAD，意思是m-格局q1（DA）和扫描一个空格（D）。变量u是格局数，随着机器运行依次是0、1、2等。包含u的是个花括号，通常意味着是个函数，虽然看起来似乎没什么意义，但很快你就将看到它很有效。

    then, for all integers n,
    and with - 图37
    那么，对于所有的整数n，
    and with - 图38

    Uγ函数的参数是格局数（0，1，2等）。图灵认为，这个函数可以转换为那个格局的描述数。我们使用描述数4来验证一下，其中需要涉及转换表达式{Uγ}(N4)，即：

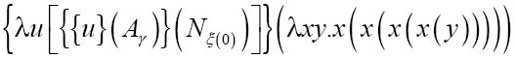
    and with - 图39

    在Uγ函数中，我使用了Nand with - 图40(0)而不是Nr，正因如此，我们不会忘记下标代表了描述数。用4的表达式替换函数中的u：

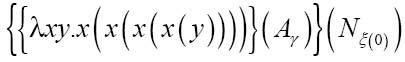
    and with - 图41

    现在将x替换为Aγ：

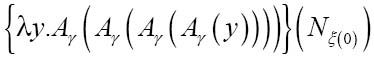
    and with - 图42

    最后我们用Nand with - 图43(0)替换y：

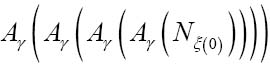
    and with - 图44

    Aγ在Nand with - 图45(0)上第一个应用的结果是Nand with - 图46(1)，下一次得到Nand with - 图47(2)，等等，因此最后的结果就是Nand with - 图48(4)，这和图灵预想的一样。现在，你就可以看出为什么将u定义为Uγ中的函数是有意义的了：它可以在根本上将出现在Aγ函数中的u混合嵌套。

    It may be proved that there is a formula V such that
    and with - 图49
    可以证明，对于公式V，有
    and with - 图50

    函数V基本上分析了连续两个完全格局的描述数，并确定打印0或者1，或者什么都不打印，这又是一个复杂但可以想到的函数。

    Let Wγ stand for
    and with - 图51
    so that, for each integer n,
    and with - 图52
    令Wγ表示
    and with - 图53
    因此，对于任意一个整数n，
    and with - 图54

    这个命题左侧的公式可以转换为N1、N2或 N3中的一个。描述这种变换比较容易，可以先描述转换后的结果：

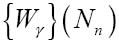
    and with - 图55

    将Wγ替换为图灵刚刚给出的那个表达式

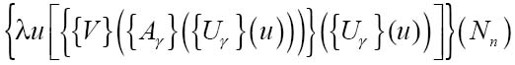
    and with - 图56

    用Nn代替u：

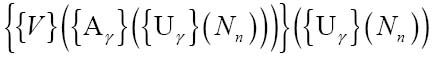
    and with - 图57

    表达式{Uγ}(Nn)可以转换为Nand with - 图58(n), 因此：

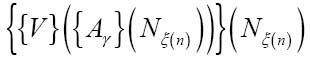
    and with - 图59

    表达式{Aγ}(Nand with - 图60(n))可以转换为Nand with - 图61(n+1)，这正是我们所求的：

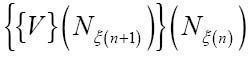
    and with - 图62

    通过这个简短的证明，我们可以知道{Wγ}(Nn)可以转换为N1、N2或 N3，这取决于第n个完全格局转换为第n+1个时打印的是0还是1，或是什么都不打印。

    and let Q be a formula such that
    and with - 图63
    where r(s) is the s-th integer q for which {Wγ}(Nq) is convertible into either N1 or N2.
    令Q是一个公式，使得
    and with - 图64
    其中r(s)是第s个整数q，其中{Wγ}(Nq)转换为N1或N2。

    在上面的公式中，最后一个N的下标明显应该是r(s)而不是r(z)。只有一部分的完全格局才会打印0或者1，函数r(s)就是用来揭示这些完全格局的。例如，如果在1、4、6、7等完全格局中打印了0或者1，那么r(1)返回1，r(2)返回4，r(3)返回6，r(4)返回7，等等。

    Then, if Mγ stands for
    and with - 图65
    it will have the required property†.
    † In a complete proof of the λ-definability of computable sequences it would be best to modify this method by replacing the numerical description of the complete configurations by a description which can be handled more easily with our apparatus. Let us choose certain integers to represent the symbols and the m-configurations of the machine. Suppose that in a certain complete configuration the numbers representing the successive symbols on the tape are s1s2…sn, that the m-th symbol is scanned, and that the m-configuration has the number t; then we may represent this complete configuration by the formula
    and with - 图66