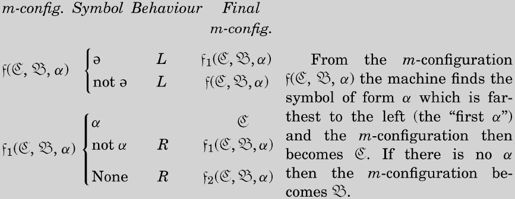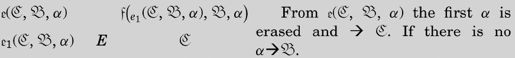每个程序员都在几乎所有的编程工作中频繁遇到某些类型的任务。有时候,这些任务是完全相同的;更多情况下,它们是有些许区别的。甚至在我们前面提到的计算2的平方根的机器中,若干m-格局都是相当相似的。例如下面三种m-格局:

在一次循环中,这些m-格局都把读写头向左移动,直到遇到一个哨兵。然后,把读写头向右移动一个位置(在最左边的数字上),接着机器转换到另一个m-格局。
预先确定机器中需要的某些相似的m-格局,并且为那些困难的工作预定义特殊的m-格局,是很有好处的。它可以帮助阐明设定图灵机时用到的策略,从而简化最终的工作。
我们把将读写头移回哨兵的m-格局称为goto-sentinel。于是,当写入某个特定机器的状态,并且想要把读写头置于哨兵右侧的数字上时,只需要给出m-格局goto-sentinel,而不用重复地阐明如何去做。这样不仅简化了机器描述,而且(从理论上)可以帮助任何查看该机器的人理解它。
我们可以就其自身来定义goto-sentinel:
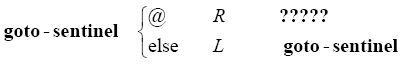
而且马上就会发现了那一连串问号指出的问题。机器在找到哨兵之后,必须转向另一个m-格局,但事实上,只有我们真的使用了goto-sentinel,机器才能知道要转向哪一个m-格局。我们需要某种指明最终m-格局的方法,以保持goto-sentinel的灵活性。
解决方法是将goto-sentinel定义成非常类似数学函数的形式,其中最终m-格局就是这一函数的参数:
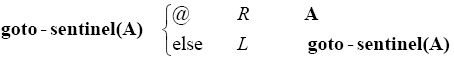
现在,我们可以不再使用new、new-digit-is-zero和new-digit-is-one这些m-格局了。在进行平方根运算的机器运行的最开始,我们不用把begin转向new,再把new转向mark-digits,可以指定:
begin none P@, R, P1 goto - sentinel(mark - digits) 也不用像下面这样把carry定义成转向new-digit-is-zero:
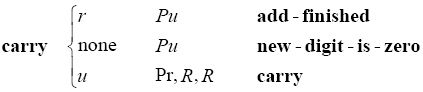
而是使之指向goto-sentinel,然后再转到print-zero-digit:

说到print-zero-digit,你是否发现它与print-one-digit相比,除了打印的数位不同,功能上是完全相同的?更好的做法是定义一般的print-digit函数,其参数就是要打印的字符:
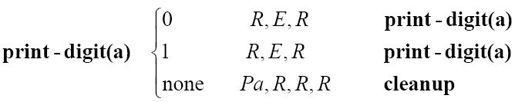
注意,最后一行的Pa操作表明,被打印的字符是print-digit的参数。此时,m-格局carry变成了:

m-格局print-new-y(用来检测什么时候应该转向格局new-digit-is-one)变为:
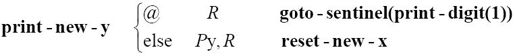
现在的程序员很快就会了解这个概念。不同的编程语言对此有着不同的说法,如程序、函数或方法,最一般性的说法是子程序。近几十年来,子程序已成为计算机程序中最通用的结构单元。
阅读本书的程序员在把他们对子程序的理解应用到这些带参数的格局上时,需要谨慎些。这些格局最初主要用来阐明图灵机的结构,并且写起来更容易。这里没有“调用”某一格局或者从一个格局中“返回”概念。
图灵在选定“m-函数”这个相对更好的术语前,把这些带参数的格局称为“骨架表”,并把使用“骨架表”的机器表叫做“缩略表”。
4. Abbreviated tables.
There are certain types of process used by nearly all machines, and these, in some machines, are used in many connections. These processes include copying down sequences of symbols, comparing sequences, erasing all symbols of a given form, etc. Where such processes are concerned we can abbreviate the tables for the m-configurations considerably by the use of “skeleton tables”. In skeleton tables there appear capital German letters and small Greek letters.
4. 缩略表
有些过程几乎所有的机器都使用,并且在一些机器中,这些过程会在很多情况下使用。这些过程包括复制符号序列、比较序列、删除某一形式的所有符号等。在使用这些过程的地方,我们可以使用“骨架表”来大大简化表中的m-格局。骨架表里通常使用大写德文字母和小写希腊字母。
令人惊讶的是,大写德文字母比它们相应的小写字母更难读。所幸,图灵只使用了A到E之间的字母,不过借助大号字体来熟悉这些大写字母还是会有帮助的:

要特别注意,字母A看上去更像U,也要留意C和E之间的细微差别。图灵在本节中使用的希腊字母是斜体的α、β和γ。
These are of the nature of “variables”. By replacing each capital German letter throughout by an m-configuration
[236]
and each small Greek letter by a symbol, we obtain the table for an m-configuration.
这些是“变量”的性质。把每一个大写德文字母用一个m-格局代替,每一个小写希腊字母用一个符号代替,我们就可以得到一个关于m-格局的表。
我在例子中使用大写拉丁字母表示m-格局,而图灵使用了大写的德文字母。我使用小写拉丁字母表示一个符号,而图灵使用的都是小写希腊字母。他的例子中通常包含多个参数。
现在的子程序(比如sqrt)保存在称为库的文件中,程序员通过指定名字来使用它们。甚至可以说,整个操作系统,比如Unix、Windows或者Mac操作系统,都主要由可供运行在该操作系统上的应用程序使用的子程序组成。
然而,对图灵来说,骨架表的存在仅仅是为了让其更大的机器更易于构建(从他的角度),并且更易于阅读和理解(从我们的角度)。
The skeleton tables are to be regarded as nothing but abbreviations: they are not essential. So long as the reader understands how to obtain the complete tables from the skeleton tables, there is no need to give any exact definitions in this connection.
骨架表仅仅是个缩略表,它们并不是必不可少的。只要读者明白了如何从骨架表中得到完整的表,这里就没有必要给出任何明确的定义了。
图灵说,骨架表不是必不可少的,的确如此。如果骨架表只是作为一个有趣的概念而提出,并且只限于论文的这一节,那么很容易被略过。然而,图灵正在为他的通用机创造条件,而通用机广泛采用了本节阐述的骨架表。如果没有这些表,对通用机的说明可能更冗长也更复杂。
因此,了解图灵的最终意图,就更容易理解这些表。正如他会在第7节要论述的,通用机解释了一条包含编码成一系列字母的计算机器的纸带。最左端是中央元音的哨兵。纸带在F-格和E-格间交替变化。E-格依然是可擦除的。在通用机中,F-格包含更多的是字母而不是数字。尽管如此,机器总是顺序地从左往右地打印F-格,且不擦除之前的符号。因此,一行中若出现两个空格,则表明那个点的右边没有F-格。
Let us consider an example:
我们来看个例子:
他本可从更简单的例子开始,但是这个例子的优点在于,它可以展示出所有的特性。图灵在表的右边给出了解释。(图灵在定义通用机的时候也把解释放在了表的右边。)
尽管图灵真正定义的是一个名为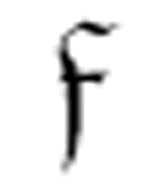 的函数,但是这个函数要求了其他两个函数
的函数,但是这个函数要求了其他两个函数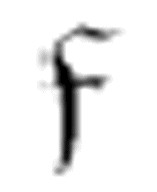 1和
1和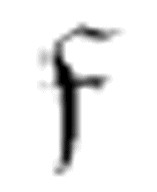 2。它们都有三个相同的参数:两个m-格局和一个符号。
2。它们都有三个相同的参数:两个m-格局和一个符号。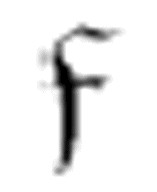 把读写头向左移动,直到遇到一个中央元音,此时m-格局转向
把读写头向左移动,直到遇到一个中央元音,此时m-格局转向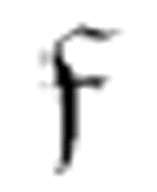 1。只要方格内不是α,读写头就向右移。(注意,α是
1。只要方格内不是α,读写头就向右移。(注意,α是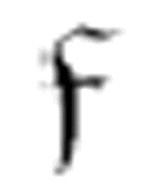 的第三个参数。)如果遇到一个α,它转到m-格局
的第三个参数。)如果遇到一个α,它转到m-格局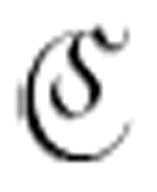 ――
――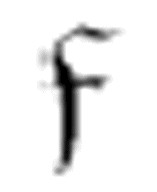 的第一个参数。m-格局
的第一个参数。m-格局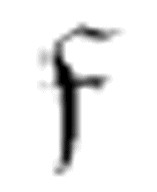 1和
1和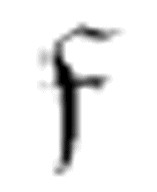 2很相似。它们一起可以有效地找到一行里连续的两个空格。当
2很相似。它们一起可以有效地找到一行里连续的两个空格。当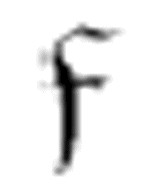 1遇到一个空格的时候,它转换成
1遇到一个空格的时候,它转换成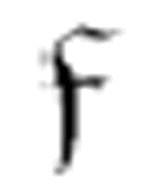 2。如果接下来的字符不是空格,它又转换回
2。如果接下来的字符不是空格,它又转换回 1。只有当
1。只有当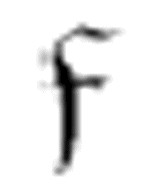 2再遇到一个空格(这个空格一定是一行中连续的第二个空格)时,则停止,并且转向m-格局
2再遇到一个空格(这个空格一定是一行中连续的第二个空格)时,则停止,并且转向m-格局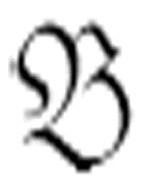 ,
,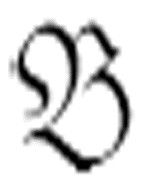 是
是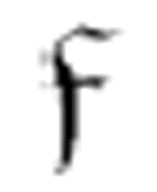 的第二个参数。在这种情况下是没有α的。
的第二个参数。在这种情况下是没有α的。
因此,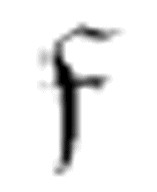 代表了find。如果它找到了α,则转向m-格局
代表了find。如果它找到了α,则转向m-格局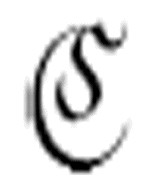 ,读写头将设置在第一个(最左边的)α处。如果它找不到α,就会转向m-格局
,读写头将设置在第一个(最左边的)α处。如果它找不到α,就会转向m-格局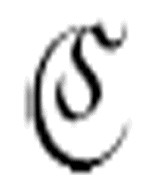 。
。
事实上,这个表里有令人困惑的地方。在两个m-格局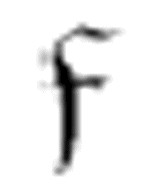 1和
1和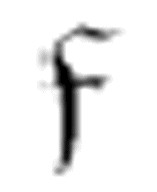 2中,“not α”的意思看上去像是“任何不是α的非空格”,因为另一个格局考虑到了“None”即空格的情况。然而,第一个m-格局不包含“None”情况,为一致起见,它应该包含这一情况。“None”应该和“not ә”[1]的情况是一样的。
2中,“not α”的意思看上去像是“任何不是α的非空格”,因为另一个格局考虑到了“None”即空格的情况。然而,第一个m-格局不包含“None”情况,为一致起见,它应该包含这一情况。“None”应该和“not ә”[1]的情况是一样的。
在一个完整机器的表里,应该采用类似下面最终m-格局列中的条目来指示骨架表:
| m-格局 | 符号 | 操作 | 最终m-格局 |
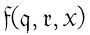
其中,m-格局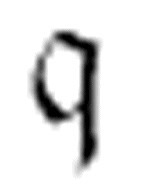 和
和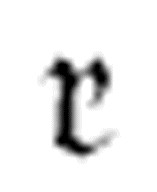 应该在机器的其他地方定义,x应该是机器使用的一个符号。
应该在机器的其他地方定义,x应该是机器使用的一个符号。
If we were to replacethroughout by
(say),
by
, and α by x, we should have a complete table for the m-configuration
.
假设把所有的用
代替,
用
代替,α用x代替,那么我们会得到m-格局
的一个完整表。
在完整机器的上下文中,这个骨架表可以有效地扩展为下表:

由于同一个机器可能多次使用函数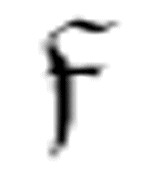 ,因此,m-格局
,因此,m-格局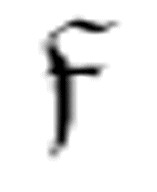 、
、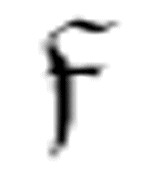 1和
1和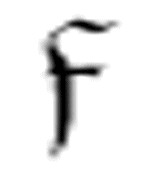 2的扩展版在每次使用时都需要不同的名字。
2的扩展版在每次使用时都需要不同的名字。
is called an “m-configuration function” or “m-function”.
被称作 “m-格局函数”或“m-函数”。
这是一个比“骨架表”更好的名字。一般情况下,我会把它们简称为函数,希望不会引起读者的困惑。
The only expressions which are admissible for substitution in an m-function are the m-configurations and symbols of the machine. These have to be enumerated more or less explicitly: they may include expressions such as; indeed they must if there are any m-functions used at all.
m-函数中允许被替换的表达式只有机器的m-格局和符号。或多或少地还是有必要明确地把它们列举出来,它们可能包括这样的表达式。事实上,如果使用了任何m-函数,则一定会包含这样的表达式。
如果已经定义了一个名为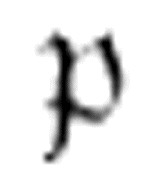 的m-函数,并且一台机器在它的最终m-格局列中引用到该函数,那么必须将
的m-函数,并且一台机器在它的最终m-格局列中引用到该函数,那么必须将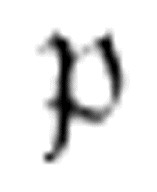 作为这台机器的m-格局来考虑。
作为这台机器的m-格局来考虑。
令图灵焦虑的是,一个m-函数的参数可以是其他m-函数。换句话说,m-函数可以嵌套。(不要担心,你会看到很多这样的例子。)问题来自隐含地允许无限递归。无限递归是指一个函数可以指向本身,或者指向第二个函数,而第二个函数又反过来指向第一个函数。如果允许无限递归,那么一个机器最后会包含无穷个m-格局,而这违背了图灵对计算机器的最初定义。
If we did not insist on this explicit enumeration, but simply stated that the machine had certain m-configurations (enumerated) and all m-configurations obtainable by substitution of m-configurations in certain m-functions, we should usually get an infinity of m-configurations; e.g., we might say that the machine was to have the m-configurationand all m-configurations obtainable by substituting an m-configuration for
in
. Then it would have
… as m-configurations.
如果我们不坚持这样明确地列举,而只是简单地声称这个机器有某些特定的m-格局(并列举出来),以及所有可以通过代换某些特定m-函数中的m-格局得到的m-格局,那么通常情况下,我们会得到无穷个m-格局。例如,假设机器拥有m-格局,以及所有可以通过代换
里的m-格局
得到的m-格局,则我们会得到如下无穷个m-格局:
,
…。
我们必须保证,在机器中代换所有的m-格局之后,得到的仍然是有限数量的m-格局。
Our interpretation rule then is this. We are given the names of the m-configurations of the machine, mostly expressed in terms of m-functions.
这便是我们的解释规则。已知的机器m-格局的名字大多数以m-函数的形式给出。
图灵又提前考虑到了他的通用机,后面可以看到,大部分通用机的确是按照本节定义的m-函数来表达的。
We are also given skeleton tables. All we want is the complete table for the m-configurations of the machine. This is obtained by repeated substitution in the skeleton tables.
骨架表也给出了。我们需要的是一张机器的m-格局的完整表,它可以通过对骨架表的重复代换操作得到。
或许在这一点上,图灵稍微有点偏执了。通常情况下,我们不需要显式地列举出机器的所有m-格局,而只需要知道有限个m-格局即可。
[237]
Further examples.
(In the explanations the symbol “rarr;” is used to signify “the machine goes into the m-configuration…”)
更多例子
(解释中的符号“→”用来表示“机器转向某个m-格局……”)
图灵把出现在骨架表右边,看上去常常很隐秘的描述称为“解释”。这些表的列都杂乱地排列在一起,而且没有列标题。有些表只包含m-格局和最终m-格局,而其他的表包含扫描字符列和操作列,它们必须根据内容的不同而有所区分。
图灵在下一个例子中,给出了一个m-函数作为另一个m-函数的参数出现的情况。
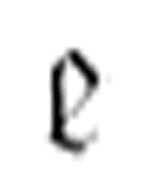 表示“擦除”。这个函数首先使用
表示“擦除”。这个函数首先使用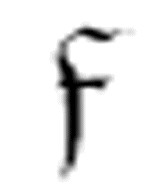 寻找(最左边)第一次出现的α,如果找到了,那么将读写头将置于这个字符上。注意,
寻找(最左边)第一次出现的α,如果找到了,那么将读写头将置于这个字符上。注意,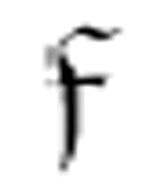 的第一个参数是函数
的第一个参数是函数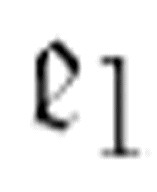 。这意味着如果
。这意味着如果 找到了字符α,它将转向
找到了字符α,它将转向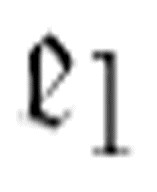 ,
,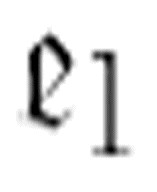 只是简单地擦除这个字符,然后转向m-格局
只是简单地擦除这个字符,然后转向m-格局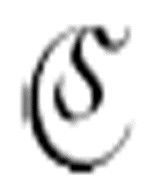 。如果
。如果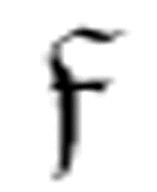 没有找到α,那么它将转向m-格局
没有找到α,那么它将转向m-格局 。
。
如果你确实仔细检查了这些情况,而不仅仅是接受图灵关于它们可以运行的说法,那么你可能会质疑为什么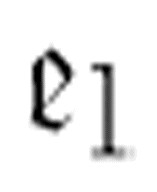 需要这么多的参数。它确实不需要这么多,它可以被更简单地定义为
需要这么多的参数。它确实不需要这么多,它可以被更简单地定义为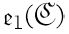 。
。
提醒程序员们:你们可能因为知道太多而不能准确地理解m-函数的嵌套。尽管难以抵制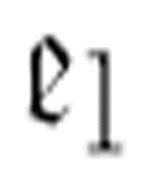 在传递给
在传递给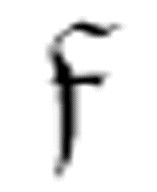 前必须以某种方式“被执行”的想法,但是我们还是要抵制这样的倾向,要把
前必须以某种方式“被执行”的想法,但是我们还是要抵制这样的倾向,要把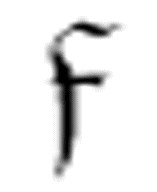 的第一个参数看作是给出了
的第一个参数看作是给出了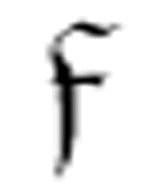 在找到α后最终转向的目的地。
在找到α后最终转向的目的地。
图灵定义了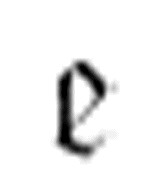 函数的第二版本,它包含两个参数,而不是三个:
函数的第二版本,它包含两个参数,而不是三个:
定义两个拥有相同的名字但根据不同数目的参数进行了区分的不同函数,是一种非常高级的编程技术,称为函数过载,这在很多老式程序设计语言中是不允许的。
两参数版本的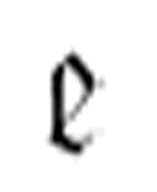 函数调用三参数版本的
函数调用三参数版本的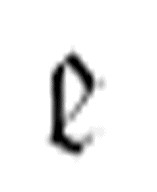 函数来擦除第一个α,但是注意,前者也可以作为后者的第一个参数。后者成功地找到并且擦除了第一个α,然后转向前者,前者继续调用后者来擦除下一个α。这个过程一直持续进行,直到所有的字符α被擦除。
函数来擦除第一个α,但是注意,前者也可以作为后者的第一个参数。后者成功地找到并且擦除了第一个α,然后转向前者,前者继续调用后者来擦除下一个α。这个过程一直持续进行,直到所有的字符α被擦除。
现在,图灵有效地利用嵌套和递归表示了重复任务的执行,这种做法是很明智的。
然而,使用两参数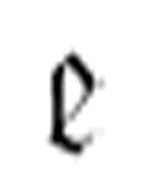 作为三参数
作为三参数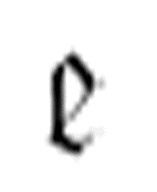 的一个参数来执行两参数
的一个参数来执行两参数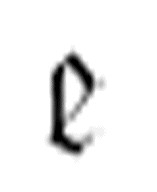 ,这样的做法看上去会让我们最担心出现m-格局无限嵌套的情形。
,这样的做法看上去会让我们最担心出现m-格局无限嵌套的情形。
The last example seems somewhat more difficult to interpret than most. Let us suppose that in the list of m-configurations of some machine there appearssay).
最后的例子看上去比其他例子更难解释。假设某个机器的m-格局列表中出现(
, x)(或许会=
)。
m-函数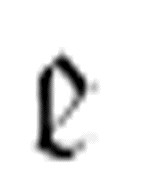 只有出现在机器的最终m-格局列中时才能在机器运行过程中发挥作用。如
只有出现在机器的最终m-格局列中时才能在机器运行过程中发挥作用。如 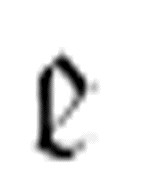 (
(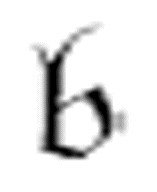 , x),其中
, x),其中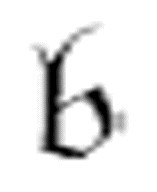 是机器中使用的m-格局。现在我们可以说
是机器中使用的m-格局。现在我们可以说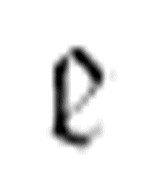 ,(
,(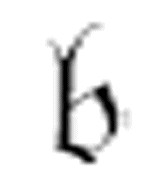 , x)是机器的另一个m-格局,并且只要我们不使用
, x)是机器的另一个m-格局,并且只要我们不使用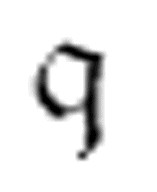 代表机器中任何其他的m-格局,我们就还可以用
代表机器中任何其他的m-格局,我们就还可以用 来表示这个新的m-格局。
来表示这个新的m-格局。
实质上,通过在机器的最终m-格局列中使用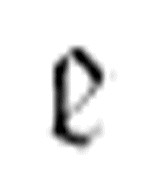 (
(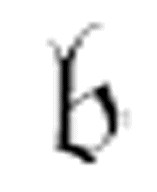 , x),我们已经给机器增加了另一个状态。图灵用两种不同的形式给出它的定义。
, x),我们已经给机器增加了另一个状态。图灵用两种不同的形式给出它的定义。