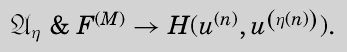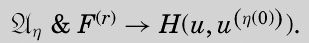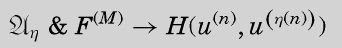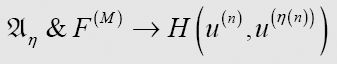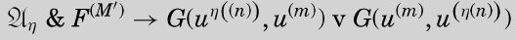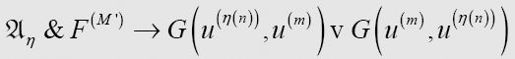and

并且，

在第一个蕴涵符的右侧是_η公理的倒数第二个表达式，用 u⁽ⁿ⁾、 u^(n-1)、u^(η(n))和u^(η(n-1))的值分别替换w、v、z和x。将这两个公式合并

Hence

因此，。

这就完成了证明的归纳部分。图灵还未证明公式在0处为真，下面就开始证明。

Also

同样，。

这仅仅是将公理的项η(0)替换成了r。现在我们知道，对于任何n公式为真。

Hence for each n some formula of the form

is provable.

因此，对于每一个n，符合下列形式的公式

是可证明的。

现在有必要证明，对于（不是图灵在下一句话中说的η(u)），公理蕴涵着H的否定。

Also, if M′ ≥ m and M′ ≥ m and m ≥ η(u), then

同样，如果 M′，那么

也就是说，如果 m≠η(n)，那么m或者大于或者小于η(n)。

[258]