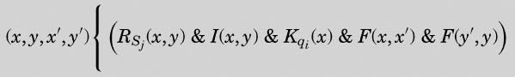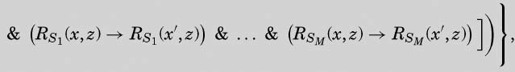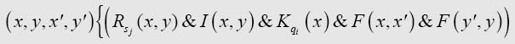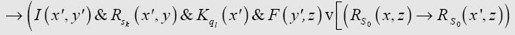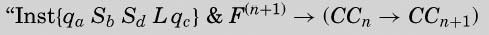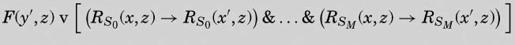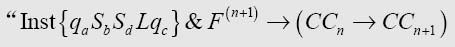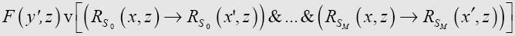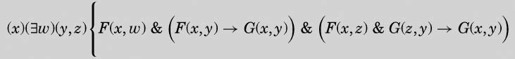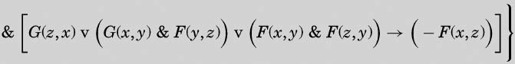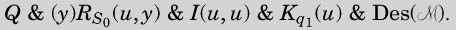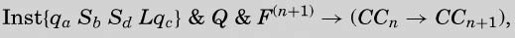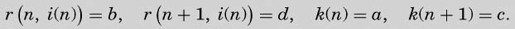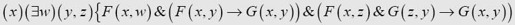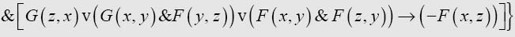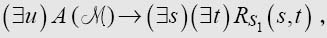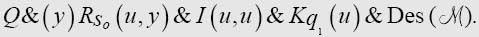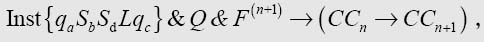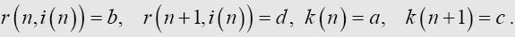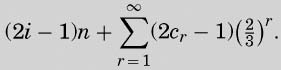第16章

对连续统的设想

历史总是试图用一系列连贯的语句和段落来捕捉生活，然而现实生活通常杂乱且复杂得多。历史学家必须磨平事实的粗糙棱角，忽略次要人物，以避免离题。这些简化有时候会扭曲它试图阐述的事物，导致一系列看上去并不自然却又不可避免的事件发生，好像任何事情都不能改变它们的发展，甚至暗示着这些事件就是所有可能中最好的结果。这些扭曲的结果有时候会称为所谓的”历史的辉格解释”——19世纪的那些作家把大英帝国的历史描绘成正在逐步、无情地走进现代议会民主制，在此之后，英国的历史学家赫伯特·巴特菲尔德（1900—1979）称之为”历史的辉格解释”。

科学史、数学史和技术史尤其容易受到“辉格解释”的影响。我们是“正确的”科学理论和“适当的”技术的受益者，因此，我们能够找到贯通历史的链条，把结果与导致其不可避免发生的原因联系起来。探索过程中的过失都被忽略了，而如果讨论的是历史争论，任何阻止我们通向即将为之庆祝的辉煌时刻的人都将被征服。

例如，在有关图灵机的历史中，人们努力将它看做一系列连贯的、逐步实现的智慧成就，从康托尔和弗雷格，到罗素和希尔伯特，再经过哥德尔、邱奇和图灵，最终在1936年发表的一篇数学论文后达到顶点。为了保持这本书内容的合理精简并且突出重点，书中也正是这么描述的。

在这个进展中，我忽略了一些异议。如同任何智力劳动领域一样，数学史上也充斥着争论与不合。^［1］在19世纪末期和整个20世纪，这些争论频繁地涉及数学哲学，特别是经常涉及无穷的本质。

数学哲学是一个广泛而又复杂的领域，不过，或许最基本的问题既简单又令人不安，那就是：

数学实体在何种程度上独立于研究它的人类。

难道数学家们只是采用与天文学家发现恒星和其他天体差不多的方式，来发现已经存在于宇宙固有结构中的数学模式吗？抑或数学家们就像工程师设计一个新的真空吸尘器，或者作曲家写一部歌剧一样来发明数学吗？伟大的数学史普及者莫里斯·克莱因（1908—1992）这样诗意地描述人们关于数学本质的疑问：

数学是那些埋藏在宇宙深处，被逐渐发掘出来的钻石吗？或者它就像人类生产的人造宝石，尽管灿烂，然而也让那些发明它们的数学家被盲目的骄傲所蒙蔽？^［2］

争论的一方是现实主义者或者柏拉图主义者，用罗杰·彭罗斯的话说： “他们相信数学真理的客观性。依我看来，柏拉图式的存在是指一个客观的外部标准的存在，它不依赖于我们个人的思想和某种特定文化。”^［3］

另一极端来自构成主义者，他们认为数学完全是由人类发明的。对构成主义者来说，数学表面上的永恒和超然存在仅仅是被人类模式识别技能加强的一种错觉，这种技能是在我们大脑中经过数百万年进化形成的。

这两个极端之间还有很多等级，每个级别都有各自的描述名称和拥护者，他们当中很可能已有部分人对我这种粗糙地在两个极端间进行分类不满了。

大多数数学工作者会把自己归类于柏拉图主义者。对数学的柏拉图式的理念支配着我们的文化，吸引着我们的本能。当我们大喊“找到了！”的时候，是表示“我发现了它”，而不是“我发明了它”。大卫·希尔伯特在第二届国际数学家大会上发表演讲之后的100多年来，我们仍然会对他的话语感到激动不已。他说：

无论这些问题看似如何地难以接近，无论我们站在它们面前感觉有多么无助，我们都坚信，经过有限步纯粹的逻辑过程之后，我们必定可以找到答案……这种对于任何数学问题都可解的坚信，对数学工作者是一种强有力的鼓励。我们听到内心不停地呼唤：存在一个问题，探索它的答案。你可以通过纯粹的推理找到答案，因为在数学里没有人类不可知的东西。^［4］

这就是柏拉图主义者的演讲，他们认为解决方法已经存在，我们只需要去寻找它们。甚至在希尔伯特关于证明完备性、一致性和判定过程的希望破灭后，柏拉图主义者的直觉仍然幸存。事实上，柏拉图主义者当中比较杰出的是库尔特·哥德尔。

数学史中的分歧不仅仅是意识形态的问题，同时也集中在适当性上。某些基本的假设构成所有数学证明的基础。然而，有一些假设是在有限对象的条件下提出的，在将其应用到无穷集合时就会出问题。

“对无穷的思考并非一帆风顺，”亚里士多德（公元前384—前322年）觉察到，我们可以想象他的学生郑重地点头表示同意，”无论你假设是否存在无穷这种事物，都会得到很多棘手的结论。”^［5］

在亚里士多德的《物理》（第三册）中，为了探究这个变幻莫测的问题，他区分了实无穷和潜无穷，这样做是很有好处的。潜无穷是自然数的无穷：每个数后面都紧跟着另一个数。把一个事物细分成越来越小的碎片也是潜无穷。存在着某些随着时间不断发生，并且永远不会结束的过程。“一般说来，事情接踵而至的时候便产生了无穷。正在发生的事件本身是有限的，但在之后总是紧接着出现与其不同的另一事件。”^［6］

然而，在亚里士多德的宇宙论中不存在实无穷，他提出几种论证解释为什么不存在实无穷。他聪明地注释道：“事实上，无穷与人们所理解的截然相反。它不是指’除本身之外没有任何事物了’，而是’除本身之外总是存在其他一些事物’。”^［7］

亚里士多德甚至不允许无穷作为一个意识层面的概念而存在：

依赖于人类大脑所想到的东西是很荒谬的，因为过度和缺陷只会存在于大脑中，而在实际世界中是不存在的。可以把我们当中的任何一个人想象得比实际大很多倍，让他变得无穷大，但是这个人并不会因为其他人这样想而变得超出常人那么大。他只能和实际一样大，如果别人想象着他也是这样大，那么只是巧合而已。^［8］

亚里士多德不是柏拉图主义者。

不是每个人都会接受亚里士多德拒绝无穷的观点。哲学家斯蒂芬·克尔纳（1913—2000）这样评论亚里士多德的理论：

它们从来不会被无异议地接受。柏拉图主义的哲学家们，包括奥古斯丁的神学家，总是将已知总体的无穷概念视为合法的，无论它们连续与否。他们不会因这个概念不适用于感官体验而苦恼，因为他们认为数学不是感官体验的抽象，更不是感官体验的描述，而是对事实的描述。事实不能通过感官理解，而要靠推理来认识。^［9］

数学家们经常被实无穷困扰着，并且试图以一种安全的方式来处理无穷过程。正是认识到实无穷和潜无穷间的区别，使得我们才能得到如下的公式

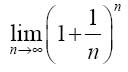
而不是

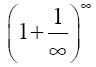
第一个公式表示了一个极限。当n的值越来越大的时候，这个表达式的值趋向于何值呢？它向我们熟知的欧拉常数靠近，约等于2.71828…。

第二个公式采用符号∞表示一个实无穷，因此根本无意义。

尽管早期的数学家们已经接近极限的定义了，但数学上极限的严格定义是由德国数学家魏尔斯特拉斯（1815—1897）提出来的。这个概念对于微积分学是至关重要的，它为微分和积分运算提供了坚实的数学基础。在极限的概念提出之前，微积分学是基于“无穷小”概念的，也就是一个非零数（因为仍可以将其视为一个有限量来操作），但是又足够接近零，使得最终可以忽略它。微积分学中仍然存在“无穷小”，例如采用dx表示这些无穷小量。

19世纪的另一位德国数学家利奥波德·克罗内克（1823—1891）极其赞赏实无穷在数学中的应用。克罗内克以其“上帝创造了整数，其他一切都是人造的”^［10］格言而闻名。提到上帝——或者更准确地说，对独立于人类而存在的数学实体的认同，使得克罗内克看上去像是个柏拉图主义者，但是从“其他一切”可以看出，他是一个绝对的构成主义者。克罗内克想把数学中的一切都建立在有限整数的有限结构的基础上，他研究的问题甚至还包括极限的概念和无理数的定义。

克罗内克从前的一位学生开始从事一项令人吃惊的数学研究——他不仅定义了无穷对象的集合，还对这些无穷对象进行了杂乱的计数，然后对这些值进行了算术运算。克罗内克反对这些方法，甚至一度阻止发表这些研究结果，导致了克罗内克对这位学生进行邪恶发狂的迫害的名声。这名学生就是格奥尔格·康托尔。

认同克罗内克的看法的人认为这种迫害更多地应该归于康托尔偏执的世界观，而非克罗内克的真实意图。^［11］然而，历史是由胜利者书写的。康托尔的集合论及其对可数集合和不可数集合的区分，后来被证明是非常有用的，因此数学史基本上抛弃了克罗内克的理论。

康托尔提出的超限数的概念是极其柏拉图主义的，甚至有点让人摸不着头脑。下面的这些话是他在1883年写下的：

我们能够从两种意义上——无论是有限还是无限——谈论整数的现实性或者存在性……首先，我们可以认为整数是实际存在的，因为基于目前为止的所有定义，我们完全都是这样理解的……但是，如果把数字看作是一个表达式，或者是对与智力相对的外部世界中事件和关系的一种复制，那么现实可以认为是由数字构成的……同时，因为彻底的现实性，我的观点也有些理想主义基础，那么在前一方面中存在的概念总是拥有以某种甚至无限种方式存在着的短暂现实，在这种意义上，我确定这两类现实总是同时发生的……这两种现实之间的关联基于我们所归属的一切的统一。^［12］

我们在前面的章节中讨论了伯特兰·罗素的逻辑主义（来自弗雷格与皮诺亚）和大卫·希尔伯特的形式主义。在20世纪早期，与它们相对的另一种运动和哲学也发展起来了，这就是直觉主义，它是由荷兰数学家鲁伊兹·艾格博特斯·杨·布劳威尔（1881—1966）提出来的。

布劳威尔是一个忧郁悲观而又神秘古怪的人，生活于20世纪初，他就像一个惊骇于所感受到的混乱的严厉校长。研究布劳威尔的学者沃尔特把布劳威尔的人生观描述为“浪漫的悲观主义和彻底的个人主义的混合体”。在早期一本名为《生活，艺术和神秘主义》（1905）的专著中，布劳威尔“痛骂工业污染和人类借用其智慧及所建立起的社会结构来主宰自然的行径，并提倡回归’自然的’、神秘而静寂的深思”。^［13］

布劳威尔考入阿姆斯特丹大学，后来在那里任教。尽管他的博士论文是关于数学基础（预示着他后来的兴趣）的，但是他的大部分早期工作都属于拓扑学领域。

布劳威尔创造了术语“直觉主义”来描述他关于如何用主观思想形式化数学实体的想法。它们都是思考的对象，它们在纸上的符号表示对于把思想从一个人表达给另一个人并无好处。相反，形式主义更注重对出现在整张纸中的符号的操作——这种做法就比一个无意义的规则下的游戏略好一点。

随着罗素和希尔伯特的纲领的逐渐形成，康托尔的工作在当时也已经被广泛接受。从布劳威尔的观点（亨利·庞加莱也持有相同的看法）来看，康托尔的集合论和超限数的广泛应用只能导致数学的灾难。

布劳威尔并不完全反对无穷的概念，他接受无穷集的构想，但前提是这些集合是可构造并且可枚举的；也就是说，它们可以一对一地与整数对应。早在1913年，布劳威尔就强调：“直觉主义只认识到可数集的存在……并且他们认为，阿列夫零是唯一存在的无穷幂”。^［14］实数集合必须被严格禁止，因为这样的集合里的元素是不可数的。定义实数集合的唯一方法是声明这种集合包含了所有的实数。你不能只展示前面的几个数，然后加一个省略号，或者定义某种包含规则。没有规则，也没有序列，你不能构造这个集合，所以也不存在这样的集合。因此，康托尔关于超限数的大部分理论“对直觉主义者毫无意义”。^［15］

1918年到1928年期间，布劳威尔发表了关于直觉论者批判形式主义纲领的文章，同时发表了一些尝试为数学提供一个摆脱问题和悖论的新基础的文章。特别地，他发现了排中律的问题。排中律是确定某一事物拥有某一个属性或者不拥有该属性，而不存在其他情况的原理。这个定律适用于有限集合，布劳威尔认为把它应用到无穷集合上是愚蠢的。

在一个著名的例子中，^［16］ 布劳威尔也相信一个收敛序列的极限总是小于零，或大于零，或等于零。（从某个意义上，这与排中律是相关的，根据排中律，这个极限或者小于零，或者不小于零。）

下面是一个数列的定义：

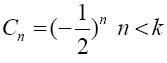
这个数列的前几个值依次是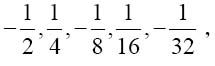，因此当n小于k时，这个数列显然是收敛于零的。并且，当n大于k时，剩余的所有c_n值均为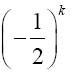，因此这即为该数列所收敛的值。

问题在于：k的值是连续数字0123456789在π在中首次出现的位置。

c_n会收敛于一个小于零的值，或者收敛于一个大于零的值，或者收敛于零吗？这取决于k是一个奇数，还是偶数，或者二者都不是。柏拉图主义者认为，序列c_n的极限是一个实实在在的数，哪怕我们不知道这个数是什么。构成主义者可能会反击说，因为这个极限是不能被构造出来的，因此它是不存在的。它是未定义的，排中律在此便不适用了。

有一次，布劳威尔在演讲关于这一不定序列的问题，有人指出，虽然我们可能不知道c是怎么收敛的，但上帝知道。布劳威尔回答道：“我可没法同上帝说话。”^［17］

我们现在已经知道布劳威尔的序列是收敛的，虽然这个事实仅仅在他死后30年就为我们所知。^［18］连续的0123456789出现在π出的第17387594880位，所以c_n收敛于2^-17387594880。既然布劳威尔原来的序列在现在已经荒废，我们很自然会想到k的另一种判别方法。我们重新定义k为π的1百万个连续的7出现的位置。因为π出看上去是以一种较均匀的方式分布在各个数位上的，所以这1百万个连续的7也许不会出现在某个地方。（也许会。虽然很多数学家相信π中能找到任何可能的数字序列，但这个观点从来没被证明。除非存在大于宇宙的计算资源，否则无法在π大中找到。）

作为拒绝无穷集合排中律的一个结果，布劳威尔还否定了一些归谬法证明的合理性，以及希尔伯特主张的任何数学问题都是可以证明的观点！

逻辑的世界同样也受到影响。排中律可以用命题逻辑表示为：

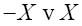
在怀特海、罗素和希尔伯特的经典逻辑体系里，这个算式等同于：

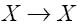
而它们都等价于：

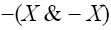
蕴涵关系X → X是古老哲学思想里的同一性（“某个事物是它自己”）的符号表示，而三个算式中最后那个则用符号表示了矛盾原理：某个事物不可能既具备某个属性而又没有那个属性。在亚里士多德逻辑学里，上面的算式代表的是不同的概念，但在命题逻辑这个“笨重的工具”的作用下，它们变成了同义词。^［19］

对希尔伯特而言，布劳威尔希望强加给数学思想的”紧箍咒”过于严厉了。希尔伯特非常不愿意放弃他的数学工具，即使他承认一些情况必须重新考虑。“我们应该小心地审视那些形成观念的方式和带来丰富多彩的结论的推理模式；我们将看护它们，支持它们，让它们更为有用，无论成功的希望有多么渺小，没有人能将我们从康托尔为我们建立的天堂里驱逐出去。”^［20］希尔伯特依然在寻找不需要使用到无穷的更为严格的证明方法。

希尔伯特和布劳威尔之间的流言蜚语渐渐升级到了顶点。1928年，布劳威尔被希尔伯特排挤出德国《数学年刊》（Mathematische Annalen）的编委位置。作为三个主编之一，爱因斯坦辞去了在《数学年刊》的职务，以此表示抗议。这次事件让布劳威尔感到万分苦闷和心灰意冷，此后十年他几乎再没有发表过论文。他在家门口被汽车撞到后不久去世，享年85岁。

我们不清楚图灵在动笔写他关于可计算数的论文前是否接触过直觉主义的思想。纽曼，这个给图灵上过数学基础课程并指导图灵发表论文的剑桥大学教授，肯定很了解布劳威尔，因为他们彼此在拓扑学上合作过。纽曼共同起草了皇家学院为布劳威尔的官方讣告^［21］（这不是一个普通的讣告，它有30页长，包括了5页对布劳威尔工作成果的介绍）。不过，纽曼只写了讣告中布劳威尔关于拓扑学研究成果的那一部分，而这也已经是在图灵的文章发表30年后的事情了。

图灵的文章很奇怪地处于形式主义和构造主义之间的孤岛上。他的机器虽然将算法限制到一系列事先定义了操作的打印符号上，但他区别实数和可计算数的方法，以及将可计算数定义为实数中那些确实可被计算的数的子集的方法，却着实有着构造主义的味道。图灵对于可计算数的定义后来导致了一门数学理论的诞生，那就是与经典的“实分析”（real analysis）理论相似的“可计算分析”（computable analysis）。^［22］

和布劳威尔的思想相似的是，计算一个数是一个随时间发生的过程。在机器还没计算到数的某一位时这一位并不存在，图灵机也不能被一个有穷的通用过程判定出可能会在未来做什么。不存在一个算法，能让你从机器的描述数中判定出机器是否会打印0或1，或者它是否会打印有限个0和1，又或者它是否会打印出连续的0123456789。如果有这样的算法，我们就可以将它应用到机器中来计算π的无穷数位，我们就可以判定机器是否会打印连续的0123456789（或者1百万个连续的7），我们就会知道布劳威尔的序列是否会收敛于0。

如果存在这样的算法，那就意味着如和π其他无理数的那些无穷数位是一种独立的柏拉图式的存在，它们不需要实际计算就是存在的。但是，这样的算法并不存在，所以我们不得不艰难地寻找以获悉每一位数字是什么。

就像你所看到的，图灵有些时候喜欢定义某些数，这些数的数位需要依赖其他机器的分析结果，这些数最后都被发现是不可计算的。布劳威尔在他1921年的论文“每个实数都有一个十进制展开吗？”（Does Every Real Number Have a Decimal Expansion?）^［23］中做了类似的事情。他定义了一个实数，它的每一位数字基于π的无穷数位上的某些数字模式出现的位置。

除了这些有趣的相似外，我在图灵1936年提交给伦敦数学学会的这篇论文中没有发现其他与布劳威尔直觉主义相似的证据。图灵的研究工作和结论是不同寻常的，我认为他并不是在某种特定数学哲学观点的条条框框下展开研究的。

1936年秋，图灵去了普林斯顿大学，和邱奇一起进行研究，随后逐渐表露出一些对数学可能性和思想的展望，其中可能包含了布劳威尔的直觉主义。

邱奇显然同直觉主义打过交道。当他1927年从普林斯顿拿到博士学位后，他曾经有两年的时间为国家研究奖学金资助的项目工作。

我在哈佛待了一年，在欧洲也待了一年。其中半年在哥廷根，因为希尔伯特当时在那里；半年在阿姆斯特丹，因为我对布劳威尔的研究很有兴趣，他的部分研究工作启发了我……我想他已经不再教书了，他显得很老。我常常得坐火车去他的住所，因为他的住所在很偏远的地方。^［24］

“显得很老”这样的描述是比较反常的：邱奇接受这段采访的时候已经80岁，而1929年布劳威尔才48岁。也许布劳威尔和希尔伯特多年前的纷争确实对他打击很大。

随后，邱奇似乎有一种考虑直觉主义的倾向（尽管不是非常坚定的直觉主义论调）。邱奇的第一篇关于λ演算的论文开头一句是：“在这篇文章里，我们为形式逻辑提出了一个公理集合，其中避免使用了自由变量即实变量，我们也引入了对排中律的某种约束，这是为了避免与超限数学有关的矛盾”。 ^［25］

邱奇的学生克莱尼的研究工作里也展示出其对直觉主义的兴趣。克莱尼在他的《数学导论》（Introduction to Metamathematics，1952）和稍后与人合作的《直觉主义数学的基础》（The Foundations of Intuitionistic Mathematics，1965）中，都包含了直觉主义的章节。一幅1953年布劳威尔的照片——摄于威斯康辛的麦迪逊，当时克莱尼在那里教书——出现在科林一篇关于递归函数理论发展历史的论文中。^［26］

图灵同时可能也受赫尔曼·外尔的影响。外尔当时在高等研究院工作。外尔在希尔伯特的指导下在哥廷根完成博士学位，在苏黎世大学教过书，并于1930年返回哥廷根继承希尔伯特的衣钵，但在1933年因为妻子是犹太人而被迫离开德国。在1919年和1928年之间，外尔一直从直觉主义的角度研究数学，从来没有失去兴趣。

图灵一次简短的从直觉主义思想出发进行的尝试出现在他在普林斯顿时发表的一篇短文里。这篇短文更正了他先前那篇可计算数论文的一些观点。我在第53页讲过，那篇可计算数论文最初发表在伦敦数学会集刊第42卷第三部分（1936年11月20日发表）和第四部分（1936年12月23日发表）。那些发表于1936年10月和1937年4月之间的部分，后来被统一作为第42卷第2系列发表。

而图灵的这篇短文出现在伦敦数学会集刊第43卷第七部分（1937年12月30日发表）。它随后又被收入第43卷的第2系列，该系列包含了从1937年5月到12月发表的文章。

[544]

ON COMPUTABLE NUMBERS, WITH AN APPLICATION TO THE ENTSCHEIDUNGSPROBLEM. A CORRECTION

By A. M. TURING.

In a paper entitled “On computable numbers, with an application to the Entscheidungsproblem”^* the author gave a proof of the insolubility of the Entscheidungsproblem of the “engere Funktionenkalkül”. This proof contained some formal errors^† which will be corrected here: there are also some other statements is the same paper which should be modified, although they are not actually false as they stand.

^* Proc. London Math. Soc. (2), 42(1936-7), 230-265.

^† The author is indebted to P. Bernays for pointing out these errors.

《论可计算数及其在判定性问题上的应用》的更正

A. M. 图灵

在题为《论可计算数及其在判定性问题上的应用^*》的论文中，作者给出了“狭义函数演算”（engere Funktionenkalkül）下判定性问题不可解的证明。这个证明包含了一些形式上的错误^†，我将在这里更正。另外，那篇文章中有几个语句的表述也需要修改，虽然它们要表达的语义并没有错误。

^* 伦敦数学会集刊，(2) 42 (1936-7), 230-265。

^† 作者感谢贝奈斯指出了这些错误。

这个3页的短文分成了两部分。第一部分对原论文第11节判定性问题不可解的证明中一些公式和表述进行了更正。我已经在第14章讲述了这些更正。为了保持完整性，以下是该短文的一部分，我只会从中打断两次。

The expression for Inst {_qiS_jS_kL_ql} on p.260 of the paper quoted should read

S₀,S₁,…,S_M being the symbols which can print.

那篇论文第260页的表达式 Inst{q_iS_jS_kLq_l}应该这样解释：

S₀, S₁,…, S_M是可以打印的符号。

这个更正其实也不怎么对。第二行的F(y′,z前的z少了一个全称量词，这个全称量词修饰整个算式的余下部分。本书第250页的版本已经纠正了这个错误。

The statement on p. 261, line 33, viz.

is provable″ is false (even with the new expression for Inst {q_aS_bS_dLq_c}): we are unable for example to deduce F⁽ⁿ⁺¹⁾→(—F(u,u″)) and therefore can never use the term

[545]

in Inst {q_aS_bS_dLq_c}.

第261页第33行的表述：

是可证明的”是错误的（就算换成新的表达式Inst{q_aS_bS_dLq_c}也是错误的）：我们不能推导出F⁽ⁿ⁺¹⁾→(—F(u,u″))，因此不能在Inst{q_aS_bS_dLq_c}中使用

这一项。

这就是图灵承认他对自然数的构建存在错误的地方。

To correct this we introduce a new functional variable G [G(x, y) to have the interpretation “x precedes y″]. Then, if Q is an abbreviation for

the corrected formula Un() is to be

where A() is an abbreviation for

The statement on page 261 (line 33) must then read

and line 29 should read

For the words “logical sum” on p.260, line 15, read “conjunction”. With these modifications the proof is correct. Un() may be put in the form (I)(p.263) with n=4.

为了更正这个错误，我们引入了一个新的函数变量G [G(x，y), 表示“x在y之前”]。于是，如果Q表示

那么更正后的算式Un()就是

其中，A()表示

第261页第33行的句子应该解释为

第29行的句子应该解释为

第260页的词“逻辑和”应该更正为“合取”。通过这些更正，这个证明将是正确的。Un() 也许应该在n=4时变形为第263页I的形式。

更正的第一部分结束后是一个空行。第二部分是关于另一内容的，涉及原文中很早出现的一个段落。

Some difficulty arises from the particular manner in which “computable number” was defined (p.233).

用某一特定方法去定义“可计算数”会引发一些困难（第233页）。

相关的这一段在本书第68页：“如果一个序列可以被非循环机计算出来，那么它就是可计算序列。如果一个数与非循环机计算出来的数只相差一个整数，那么它就是可计算数。”

图灵在下一句话中的“直觉”一定指的是它的原意。如果图灵想表达任何同布劳威尔有关的意思，他应该会使用“直觉主义”一词。此外，从后面一句话中显然可以看出这个假设并不满足直觉主义的条件，即使它符合直觉认识。

If the computable numbers are to satisfy intuitive requirements we should have:

If we can give a rule which associates with each positive integer n two rationals a_n, b_n satisfying a_n ≤a_n+1 <b_n+1≤b_n, b_n - a_n < 2^-n, then there is a computable number α for which a_n ≤ a ≤ b_n each n.

(A)

如果可计算数满足我们的直觉要求，那么有：

如果我们可以给出一个规则，对于每一个正整数n，都有两个有理数a_n和b_n，满足a_n ≤a_n+1<b_n+1≤b_n,b_n-a_n<2^-n, 那么对于每个n都存在一个可计算数α，

a_n≤a≤b_n。

(A)

对于直觉主义而言，“规则”就是构造法。对于从0开始的n，2^-n等于二进制数1, 0.1, 0.01, 0.001,等等，所以这个规则的结果是一列相邻距离逐渐接近的有理数列——对于每一个新的n值，距离的值都小（右移）了一位。通常我们将这个序列称为收敛序列。

A proof of this may be given, valid by ordinary mathematical standards, but involving an application of the principle of excluded middle.

按一般意义上的数学标准，可以对此给出一个有效的证明，但要涉及排中律的应用。

问题是这个规则的结果包含了一些无法通过某种方法确认的东西，例如π的无穷展开式中符合特定规律的连续数字。图灵稍后会给出一个更有图灵特色（Turingesque）的例子。

On the other hand the following is false:

There is a rule whereby, given the rule of formation of the sequences a_n, b_n in (A) we can obtain a D.N. for a machine to compute α.

(B)

从另一方面而言，下面的说法是错的：

存在这样一个规则：如果给定(A)中可以形成序列a_n和b_n的那个规则，那么可以得到一个描述数，一台机器将可以使用这个描述数计算α。

(B)

注意，他认为这个说法是错的。

That (B) is false, at least if we adopt the convention that the decimals of numbers of the form m/2ⁿ shall always terminate with zeros, zeros, can be seen in this way.

至少如果我们采用这一约定，即形如m/2ⁿ的数的小数形式以零结尾，则(B)是错误的，这一点可以从以下方式中看出：

形为m/2ⁿ的数是有理数的子集，它们和图灵机有特定的联系，因为这样的数用二进制表示将只有有限个1。例如，有理数12345/65536用二进制表示是：0.0011 0000 0011 1001 0000…，因为65536是2¹⁶，只有小数点后面的前16位二进制数可能是非0的（取决于分子），其余位都是0。任何m小于2ⁿ的形如m/2ⁿ的数字都以至多几个非零二进制数位开始，以无限个零永远继续下去。

图灵将会给出一个构造a_n和b_n的规则，但是这个规则基于的是另一台机器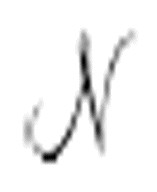所打印出来的序列。

Let be some machine, and define c_n as follows: c_n = if has not printed a figure 0 by the time the n-th complete configuration is reached c_n = - 2^-m-3 if 0 had first been printed at the m-th

[546]

complete configuration (m≤n). Put a_n = c_n - 2^-n-2, b_n = c_n + 2^-n-2.

令表示某个机器。定义c_n为：如果在第n个完全格局时还没有打印出符号0，则c_n =；如果在第m（m≤n）个完全格局时第一次打印了0，则c_n =-2^-m-3。定义a_n = c_n - 2^-n-2, b_n = c_n + 2^-n-2。

让我们看看例子。假设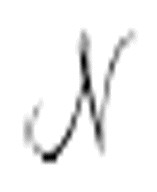是一台打印序列1111101…的机器。下面是c_n、a_n和b_n的计算过程。

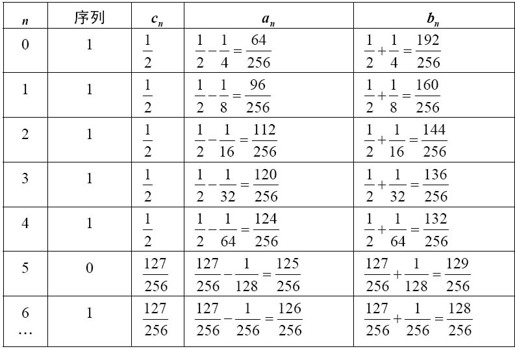
在第一个0出现在序列里之前，c_n都是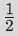。如果第一个0出现在序列中的位置是m（例子里是5），那么在n大于或等于m的情况下，c_n就等于(2^(m+2)-1)/2^(m+3)。

Then the inequalities of (A) are satisfied,

那么(A)中的不等式成立。

a_n的值总是在增加，b_n的值总是在减少，a_n和b_n差的绝对值总是小于2^-n。（实际上这个差总是2^-n-1。）

and the first figure of α is 0 if ever prints 0 and is 1 otherwise.

如果打印出0，那么α的第一个符号是0；如果没有打印出0，那么α的第一个符号就是1。

在上面的例子里，极限显然是127/256，所以机器计算出来的α序列是011111110000…，表示那个有理数。如果在n等于4的时候序列出现了第一个0，那么极限是63/128，α序列就是011111100000…。仅当0从不在序列里出现的时候，极限才是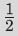，这时候序列等于100000000000…。

我们现在显然有了计算a_n和b_n的规则，但是这个规则建立在由其他机器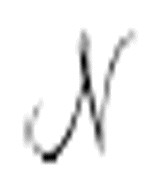打印出的序列基础上，这样的规则需要有一个过程去判定像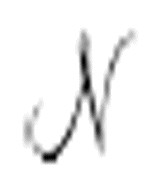这样的机器是否会打印出0。

如果从未打印0，那么α的第一个符号是1；如果打印过0，那么α的第一个符号是0。于是，

If (B) were true we should have a means of finding the first figure of α given the D.N. of : i.e. we should be able to determine whether ever prints 0, contrary to the results of §8 of the paper quoted.

如果(B)是正确的，给定的 D.N.，我们就有方法可以找到α的第一个符号，即我们将能够判定是否打印过0，这与所引用论文中§8的结果是矛盾的。

这里的“引用论文”指的是图灵的原始论文。接下来的一句话有点让人震惊，它乍看上去好像是错误的（就像我初见之时一样）：

Thus although (A) shows that there must be machines which compute the Euler constant (for example) we cannot at present describe any such machine, for we do not yet know whether the Euler constant is of the form m/2ⁿ.

这样，虽然(A)表明肯定存在一些机器能够计算像欧拉常数这样的数，但我们目前还描述不出任何这样的机器，因为我们并不知道欧拉常数是否是m/2ⁿ的形式。

图灵在这里提到的欧拉常数并不是作为自然对数基的那个e，而是不怎么著名的欧拉常数γ（gamma），它的计算式是：

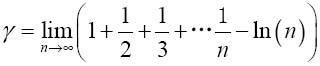
或者换一种更有启发性的表达式，即是函数l/x的和式与积分的差：

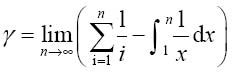
其近似结果是0.57721566490153286…。

这个欧拉常数也称为欧拉–马歇罗尼常数。欧拉在1734年提出计算这个常数的公式，并在1781年计算出了这个常数的前16位。马歇罗尼（1750—1800）之所以在这个常数上留了名，是因为他在1790年将它精确到了前32位（虽然只有前19位是正确的），并第一次用字母γ来表示这个常数。^［27］

图灵并不是随意选择这个常数的，这个常数最著名的一个性质是，没有人知道它是有理数还是无理数。也没人知道，如果它是无理数，那么是代数数还是超限数。1937年人们不知道，直到2008年，人们依然不知道。

本章开头引用希尔伯特的话时提到了“难以接近”的问题。实际上，应该在那句话前加上：“考虑任何铁定未解的问题，如欧拉考马歇罗尼常数C是否是无理数，或者是否存在无穷多个形如2ⁿ+1的素数。无论这些问题看似如何地难以接近……”欧拉—马歇罗尼常数被认为如此地难以接近，以至于希尔伯特并没有把它列入新世纪数学界要挑战的23个难题之中。

如果欧拉常数是有理数，那么它的分母可能是2的幂次方。如果这样，它的二进制表示将以无尽的0结尾。

如果用一台图灵机计算γ，显然没有通用过程可以判定γ是否形如m/2ⁿ，因为这相当于判定这个机器是否能打印出有限个1，而这是不可能的，这很清楚。

图灵提出了一些更为严重的问题：必须知道欧拉常数是不是有理数，才能定义计算欧拉常数的图灵机，即图灵机自己必须“知道”γ是否以无尽的0结尾。这让那些真正动手编写算法计算γ的成千上万位数的人很惊奇。

不过，图灵机有一个关键点，它和图灵机不能消除已经打印的符号有关：当一个数字是m/2ⁿ形式（m小于2ⁿ）时，我们期望图灵机在前n位后都打印0。但一台计算欧拉常数的机器并不会这样做，因为计算欧拉常数的算法会用越来越小（但有限的）的项去逼近它。如果欧拉常数确实是m/2ⁿ的形式，机器为了计算它的确切值就必须知道这点。否则，机器只会不停地逼近，因为它的逼近目标不是精确固定的。前n位之后的非0位就是错的，而且很成问题，因为这些位在图灵约定里是不能擦除的，但这些非0位又是不可避免的。

不管你如何欣赏图灵对欧拉常数问题的这番精彩的分析，都可能会发现他的解决方案比问题本身更糟糕。

This disagreeable situation can be avoided by modifying the manner in which computable numbers are associated with computable sequences, the totality of computable numbers being left unaltered. It may be done in many ways^* of which this is an example.

^* This use of overlapping intervals for the definition of real numbers is dud originally to Brouwer.

通过修改可计算数与可计算序列，或者与其余不被改变的可计算数的总和的联系，可以避免这种令人讨厌的情形。这可以用多种方法^*实现，下面是一个例子。

^* 这种使用重叠区间定义实数的方法最初源于布劳威尔。

如果笼罩在该节论文上的直觉主义气息在之前还不够明显的话，那么这里的脚注直指布劳威尔对实数的定义就是最好的证明。

实数的连续统一直以来都是个充满问题的概念，因为它同时涉及离散和连续两方面的性质。每一个实数在连续统上似乎都是精确的一点，但如果说连续统是由所有这些离散的点组成的，又会让人觉得很不舒服，特别是在康托尔告诉我们这些离散的点甚至都不可数以后。

布劳威尔尝试用一种既保留连续统的连续和离散性质又可以避免实无穷的方法来定义实数。

布劳威尔为这一过程发明的工具就是“选择序列”。选择序列有几种变形，但为了构造一个实数，它们都是有理数对的无穷序列，每个后续对定义了嵌套在前一间隔内的间隔。例如，下面是一个可能的选择序列，每个括号里表示一个嵌套的有理数对。

[3,4]

[3.1,3.2]

[3.14,3.15]

[3.141,3.142]

…

从经典意义上说，这个选择序列是在收敛的，我们激动地发现它似乎收敛于π。然而，在谈及布劳威尔的选择序列时，有必要避开“收敛”的概念，因为它暗含实无穷的意思。这个序列的每一个元素定义了两个端点间的连续区间。选择序列通过这样保持连续的性质。这个选择序列并没有极限π。相反，它保持着一个叫做halo^［28］的类型，它在的的附近。当序列越来越长，区间越来越小的时候，这个halo会变得越来越小，但halo永远不会收缩到精确的无量纲无理数无π上。

一位布劳威尔学者如此解释布劳威尔的选择序列和传统极限的不同：

有必要强调，选择序列直观上是随着时间而增长的，它本身就是实数……在布劳威尔的解释里，人们能够很好地理解实数，因为它就是这个不断随时间增长的序列本身。选择序列并不是用来逼近超真实里的实数的方法。^［29］

在直觉主义的连续统里，实数总是不完全的——没有终点，永远不会终结，并展现出一个非0的维度。

上面展示的选择序列可以由一些算法生成，因此它也叫做“似定律”（lawlike）选择序列。也有一些“非似定律”选择序列，其中的每个元素是由一些决定序列如何发展的代理（如数学家）选择的。数学家甚至通过抛硬币来决定选择序列中的元素。

我们可以将非似定律选择序列看成一种直觉，即使它与似定律的直觉在某些方面相当不同。非似定律选择序列依然是一个主体（subject）或超越自我（transcendent ego）随时间执行的序列，其中只有一部分是确实完成的。事实上，我们只完成了它的有限的初始段，非似定律选择序列就像朝着实数的方向不停地勾勒地平线（但地平线的那边还有地平线）。我们应该把它看成一种“自由转换的手段”。应该指出，我们这里说的选择序列是一种过程，一种随时间演化的行动序列。^［30］

选择序列也可能是似定律和非似定律选择序列的组合。例如，在多个非似定律选择序列上执行事先确定的算法操作。

如果两个选择序列从相同的元素开始，并持续保持一段时间的相等，那么它们可以视为相等。例如：

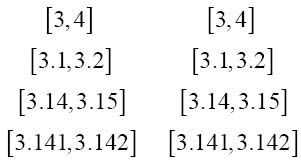
过了一段时间，这个序列可能变得不相等，而是区间重叠了：

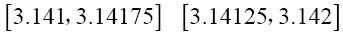
或许再过一段时间，序列又相等了：

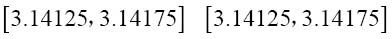
接下来会发生什么，我们只能去猜。

这样看来，似乎似定律选择序列可以由产生它的算法完全定义，因此它能表示连续统上的离散点。

即使这样，对于选择序列表示直觉主义连续统上一点的正确理解应该是，这个选择序列必须看作是进行中的选择序列，不管它是似定律的或非似定律的。对于非似定律选择序列，这点比较容易理解；对于似定律序列，这点也应该相同。否则，如果把似定律选择序列看成完成的对象，那么我们又会被引入用经典的原子论观点看待直觉主义连续统上的点的圈套里，这样连续统就会中断。换句话讲，直觉主义连续统上的点永远不表示“是什么”，而表示“变为什么”，连续统通过这个性质而保持。^［31］

读过图灵论文的读者应该感到上面的这些概念有点熟悉，因为我们了解了图灵机。考虑一个能表示实数的图灵机（或者它的描述数），但是这台图灵机总是经过一段时间才打出一些数位符号。它永远不会终结，我们永远不可能通过它的描述数判定这个实数将变成什么样。二进制的读π/4是：

110100100001111110110101010001000…

（我之所以用（π/4而不是而/是因为为π/4在0和1之间。）一台计算之π/4中各个数位的图灵机可以看成是在计算它的选择序列。当机器计算到第一位1时，这一位并不表示数字0.1，它表示的是从0.10000000…到0.11111111…的区间，因为这是开头为0.1的实数可能所在的范围。记住，序列0.11111111…等于1，于是这台机器计算产生的嵌套的选择序列是：

[1.1,1.0]

[0.11,1.00]

[0.110,0.111]

[0.1100,0.1101]

[0.11001,0.11010]

[0.110010,0.110011]

[0.1100100,0.1100110]

…

在这个意义上，一台普通的遵守图灵约定（也就是不会擦除已经打印的符号）的图灵机，会产生一个表示可计算实数的布劳威尔选择序列。这个过程一直持续，不会终结。

如果图灵在世，用我的方法来看待上述这种巧妙的联系，他是不会认可的。诚然，他没有我今天的条件，能够看到21世纪学者对布劳威尔那些晦涩文章所作的解读。如果那时图灵读过布劳威尔的文章，或者通过间接渠道获得布劳威尔的思想，那么这篇文章可能会变得与布劳威尔1928年的论文《连续统的结构》（Die Struktur des Kontinuums）相似^［32］。布劳威尔的论文讲的是将选择序列作为一种树形结构，通过重叠区域去覆盖连续统中的片段。这可能会让图灵想到，如何将可计算序列转换为可计算数。另外，为了解决欧拉常数的问题，图灵还可能考虑将其机器的计算范围扩展到0和1区间以外，因为他的机器那时只能计算0和1区间内的数。

在图灵原始的想法里，只要加一个二进制小数点，一个可计算序列就变成了实数。不过，修订后的论文里的表述更为复杂一些。

Suppose that the first figure of a computable sequence γ is i and that this is followed by 1 repeated n

times, then by 0 and finally by the sequence whose r-th figure is c_r; then the sequence γ is to correspond to the real number

假设可计算序列γ的第一个数是i，它之后跟着n个连续的1，然后是0，最后是一个第r个数是c_r的序列，那么这个序列γ对应的实数就是：

符号i表示数的正负号：0表示负号，1表示正号。n个连续的1表示数的整数部分。0起到分隔作用，它的功能就像一个二进制小数点。接下来的那个序列表示数的小数部分，它的形式总是为：

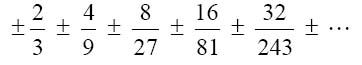
其中c_r表示每一项是正号（等于1时）还是负号（等于0时）。

例如，一台机器打印出下面的序列：

1 111110 11011…

我在数字间留了空隙，是为了便于转换。它的第一位是1，表示是个正数。接下来的5位是连续的1，以0结尾，所以正数部分是5。小数部分是：

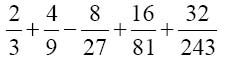
在这一步后已经完成的数字是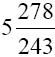或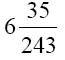。注意，被计算的这个数字的整数部分是6而不是5。如果表示小数的那些数位全是1，那么小数部分就是：

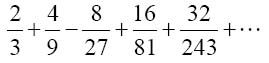
它收敛于2。类似地，如果表示小数的那些位全是0，那么小数部分收敛于，2。一个整数部分被编码为N的序列其实可以还原为N-2到N+2，相当于创造了一个重叠区间。

If the mechine which computes γ is regarded as computing also this real number then （B) holds.

如果计算γ的机器也可以看成是计算这个实数，那么(B)成立。

也就是说，如果存在一个规则可以公式化表达接近某个数的序列a_n和，b_n我们就可以得到这台机器的描述数。机器在内部计算a_n和b_n，然后根据是减去或加上(2/3)ⁿ才能使计算出的数在新的区间范围里来选择打印0或者1。

在这个过程中，我们只能通过单一的、基于收敛边界的方法来计算数。我们再也没法用一台简单的机器来计算像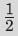或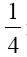这样的有理数。这些数必须像其他数那样通过逐渐逼近来计算。例如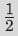，的序列现在是：

001010 1101 0100 1101…

前两位表示正号和二进制小数点。后面的几位表示2/3, -/4/9, 8/27, 416/81，等等。这里给出的这部分序列用大于3位十进制或者10位二进制的精度来表示。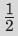

这种做法的优点是，机器不需要知道它正在计算的是一个有着m/2ⁿ形式的有理数。它不需要知道该什么时候放弃计算而在末尾加无穷的0。即使一个以无穷的0或1结尾的序列也要与一个表示为无限个递减但有有限个项的数相对应。

还有另一些方法计算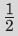。下面是其中一种：

0 10 0101 0010 1011 0010…

第一位表示正号，接下来的两位表示数字1。再接下来的几位表示再-2/3, 4/9, -/8/27, 16/81等项，刚好与前面第一个序列相反。

The uniqueness of representation of real numbers by sequences of figures is now lost, but this is of little theoretical importance, since the D.N.'s are not unique in any case

The Graduate College,

Princeton, N.J., U.S.A.

通过数字序列来表示实数的方法现在并不唯一了，但从理论上讲这并不重要，因为任何情况下描述数都不是唯一的。

研究生院

普林斯顿，美国新泽西州

这就是图灵这篇短文的全部内容。图灵这次对假设和推理的改变给我们带来的那点迷惑似乎并不遗憾。现在，我们有了一个对可计算数的不怎么繁琐的数学定义，这或许会让我们稍感满足，但是依然很难弥补我们从哲学角度对连续统问题茫然无措的迷失感。

对连续统的设想