在如今这个数字化时代,我们已经习惯于将各种形式的信息都表示成数字。文本、图画、照片、声音、音乐、电影,万物都可以进入数字化工厂,以0和1构成的更为复杂的形式保存在计算机和其他设备上。
但是,在20世纪30年代,只有数才算是数字,如果某个人把文本转换成数字,其目的是欺骗和耍阴谋。
1937年秋,阿兰·图灵开始了他在普林斯顿第二年的生活,当时英国和德国之间很快就要爆发一场战争,普林斯顿处于高度恐慌中。当然,他那时正忙于博士论文,也已经对密码学有了兴趣。密码学是涉及科学和数学领域的学科,它创建保密码(密码学)并破解他人代码(密码分析学)。[1]图灵坚信,战争期间,加密信息的最好方式是将单词转换成二进制数字,然后再乘上很大的数字。在不知道那个大数字的情况下,解密信息会涉及很困难的因式分解问题。图灵的这种想法很有先见之明,因为如今大多数这种计算机加密的工作就是这样的。
与大多数数学家不同的是,图灵喜欢亲自动手做事情。为了实现自动的编码机器,他用电磁式继电器制作了一个二进制乘法器。在人们证实电子管足够可靠之前,电磁式继电器是计算机的基本构件。图灵甚至到机械工厂亲自制造继电器,亲手缠绕电磁铁。
当时,德国的陆军和海军已经在使用一种完全不同的加密设备了。一位名叫亚瑟·谢尔比乌斯(1878—1929)的德国电气工程师发明了恩尼格玛密码机(Enigma)。1918年,谢尔比乌斯试图说服德国海军使用这个机器,但是失败了。1923年,恩尼格玛密码机用于商业用途并出售。之后,德国海军很快对它产生了兴趣,最终其他军队也相继开始使用它了。[2]
恩尼格玛密码机有一个类似打字机的26个按键的基本键盘,但没有数字、标点和移位键。键盘上方是以同样形式排列的26个灯泡。信息通过键盘输入时就会被加密。每按下一个字母,另一个不同字母的灯泡会亮起来。这些亮起的字母被手工抄下来,然后发送到收件人那里。(加密的信息可以由人亲自传送,或者通过邮件发送。再后来,人们使用摩尔斯电码通过无线电传输加密信息。)接收信息的人也拥有一台恩尼格玛密码机,他会在键盘上输入加密信息,闪光的灯即可显示出原始的文本。
键盘按键通过一系列转子与灯泡实现电气连接。每个转子都是每边有26个触头的小圆盘,这些触头代表了字母表里的26个字母。在转子里面,这些触头是对称连接的。比如,如果左边的触头A与右边的触头T连接,那么左边的触头T就将和右边的触头A连接。正是这种对称的连接关系,使得机器既用来加密,也用来解密。
标准的恩尼格玛密码机有三个连接的转子,它们的布线都不一样,每一个都可以设置到26个位置中的一个。加密机器和解密机器上的这三个转子的布线必须完全一样。依照只有恩尼格玛密码机操作员知道的键列表,这些由三个字母组成的设置转子的键可以每天改变。
至此,我对恩尼格玛密码机的所有描述都只能是让它简单地替换字母,这种加密方式即便是最业余的密码破译者也可以轻易破解。它甚至比大部分其他通过字母替换来加密的方式都更简单,因为它内部的连接是完全对称的。也就是说,如果D被加密成S,那么S也相应地被加密成D。
但事实并非如此。每当恩尼格玛密码机的用户在键盘上按下键,转子都会移动。每按下一个键,第一个转子都会向前移动一个位置。比如,如果键入一个包含26个字母A的字符串,那么随着转子在26个位置上的移动,每个A都会被编码成不同的字母。当第一个转子完成了一圈完整的变化后,第二个转子就会向前移动一个位置。接下来,另一个包含26个A的字符串又会被编码成另一串不同的字母。同样地,当第二个转子完成一个循环后,第三个转子又会向前移动一个位置。第四个固定的转子会使电信号按相反方向再次经过这三个转子。只有进行了17576次按键(26的三次方)后,加密模式才会重复。
问题不仅在于此,这些转子是可替换的。机器配备了五个不同的转子,每个转子都可以随意放置在三个转子空位中的任何一个。另一个加强方法是加上一个插接板,这又增加了一层字母混杂。
1932年,三位波兰数学家开始寻找破解恩尼格玛信息的方法。[3]他们认定需要构造可以自动模拟恩尼格玛编码的设备。第一台设备bomb(他们这样称呼)在1938年开始运行,其工作方式就是搜索所有可能的转子设置。其中一名数学家是马里安·雷耶夫斯基(1905—1980),毕业后他在哥廷根度过了一年。他写道,由于“找不到更好的名字”[4],他们把那些机器叫做bomb,不过也有可能是因为机器发出的嘀哒声而得此名,也或许是用这些数学家们喜欢的某种冰淇淋圣代命名的呢。[5]
英国政府传统上是雇用一些古典文学学者来从事解码工作,因为他们认为这些人在解读困难语言方面受过最好的训练。随着战争的临近,为了分析类似恩尼格玛的复杂编码设备,政府编码与密码学院(GS&CS)显然也需要数学家。
1938年夏天,阿兰·图灵从普林斯顿返回到英国后被邀请到GC&CC总部做讲座。英国政府可能早在1936年就和他有了联系。1939年,GC&CC购买了一处地产,其处有一座坐落在伦敦东北50英里叫做布莱切利庄园的维多利亚时期官邸。[6]在某种意义上,布莱切利庄园是整个英格兰智慧的焦点,牛津大学和剑桥大学间的铁路线和向南通向伦敦南部的铁路线在这里交汇。
1939年9月1日,德国入侵波兰。两天后,英国向德国宣战。9月4日,阿兰·图灵到布莱切利庄园报到。最后,大约有一万人在那里进行拦截和破译秘密通信的工作。为了容纳每一个人,官邸周边建造了临时营房。图灵负责管理8号营房,致力于破译德国海军的密码。德军使用这些编码与潜水艇进行通信,这些潜水艇对驻扎在美国和英国间的大西洋护航舰队极具威胁。
早在1939年,英国政府就会见了一些波兰数学家,向他们了解恩尼格玛密码和bomb。图灵来到布莱切利庄园后不久,便开始重新设计并改进这些设备,也就是现在的bombe(法文)。1940年,第一台“图灵Bombe”(他们有时候这么叫)开始运行。它有一吨重,可以模拟30台并行运行的恩尼格玛密码机。[7]
在使用“图灵Bombe”攻击加密信息之前,有必要降低可能性范围。破译人员寻找crib,即那些在加密信息中经常出现的词汇或词组。它们可以确定第一个转子的位置。相同的信息被编码成两种形式进行传输的情况更有价值,它们被称作kisses。另一种技术是在各种宽度的厚白纸上打印多行字母,这与后来计算机里使用的打孔卡片很相像。分析员根据加密信息的字母在纸上打孔。通过把纸张重叠在一起可以比较同一天内获取的不同信息(它们都基于恩尼格玛的同一套格局)。因为这里使用的纸张来自附近名为班伯里(Banbury)的镇,因此这个过程称作banburismus技术。
到1941年中期,这些多样的技术经过改进,最终成功破译了恩尼格玛加密的通信,并大大降低了海军的损失。[8]阿兰·图灵在其中起到了至关重要的作用,当然在布莱切利庄园工作的很多人也理应为此受到称颂。
甚至在布莱切利庄园这样由数学家和古典文学学者构成的不寻常人群中,图灵依然因性格怪异而博得了一定的名声。
每年六月的第一周,图灵都会得一场严重的枯草热病,他会戴着军用防毒面具来遮蔽花粉,然后骑自行车去办公室。他的自行车有个毛病,车链每隔一定时间就会脱落。图灵不去修理它,而是数脚踏板转的圈数,然后赶在车链掉下之前下车,用手调整车链。[9]
1941年春,阿兰·图灵向琼·克拉克求婚,她是布莱切利庄园里为数不多的从事那种需动脑筋的文书工作的一位女性。琼·克拉克在被聘来做解码工作前在剑桥大学研究数学。求婚几天后,图灵向她坦白自己有同性恋倾向,[10]但是婚约还是维持了几个月,直到最后他觉得不得不取消它。
1942年11月,图灵前往华盛顿帮助协调英国和美国之间的密码破译工作。那次任务之后,他在贝尔实验室度过了第二年的前两个月,当时贝尔实验室设在纽约市西街。他在那里遇到了开辟数位采样理论的哈利·奈奎斯特(1889—1976)和克劳德·埃尔伍德·香农。香农的论文“通信的数学理论”(1948年)开创了信息论这一领域,他还引入了”比特”的概念。
图灵在贝尔实验室关注的是一台语音置乱设备,它主要用来保证大西洋上的电话通信安全。声波被分解至不同的频率范围,然后被数字化,最后通过模数加法来加密,这是一种不超过某一个特定值的加法(比如分钟值和秒值相加时,这个值是60)。在接收端,这些数字被解码,然后重新构成语音。
在奈奎斯特的研究、香农的论文以及语音加密设备中,我们可以看到后来引发将图片数字化为JPEG文件和将声音数字化为MP3文件等技术想法的最初由来。但是这些创新需要几十年才能变得成熟。另一方面,最早的数字计算机基本上只能处理数字,甚至连巴贝奇最初发明的差分机都只能用来打印无差错的对数表。在这个背景下,图灵机只能生成数字,而不能做其他的事情,比如不能执行普通函数,就一点也不令人惊讶了。
图灵即将通过使用数字加密其他形式的信息来把他的论文引向更不寻常的方向。他在论文的下一节论证了数字如何来表示机器本身,而非照片或歌曲。
的确,万物皆数字,甚至连图灵机本身都是数字的。
5. Enumeration of computable sequences.
A computable sequence γ is determined by a description of a machine which computes γ. Thus the sequence 001011011101111…is determined by the table on p. 234, and, in fact, any computable sequence is capable of being described in terms of such a table.
5. 可计算序列的枚举
一个可计算序列γ是由计算γ的机器所描述。因此,序列001011011101111…是由第234页的表决定的。事实上,任何可计算序列都可以通过这样的表来描述。
那是本书第75页的例子II中的机器。
It will be useful to put these tables into a kind of standard form.
把这些表转换成一种标准形式是很用的。
事实上,图灵就是从第1节(本书第58页)描述的标准形式出发的。他指出,某种操作可以让机器打印或擦除符号,也可以把一个格移到左边或右边。在展示了一台这种形式的机器(本书第69页的例子I,也是图灵马上要提到的例子)后,图灵很快放弃了自己的规则。他允许一次操作打印多个字符,或者移动多个格。这些操作可以单独执行,因此机器表不会有几页长。现在他回到了他最初的约定上。
In the first place let us suppose that the table is given in the same form as the first table, for example, I on p. 233. That is to say, that the entry in the operations column is always of one of the forms E: E, R: E, L: Pα: Pα, R: Pα, L: R: L: or no entry at all.
首先,我们假设表仍以第233页例I中的形式给出。也就是说,操作列的条目总是下列形式之一:E: E、R: E、L: Pα: Pα、R: Pα、L: R: L,或者没有任何条目。
图灵使用冒号来分隔九种不同的可能性,这些可能性来自于三种类型的打印(擦除、打印字符,或者两者都不是)和三种移动(向左、向右或者不移动)的结合。
The table can always be put into this form by introducing more m-configurations.
通过引入更多的m-格局,总是可以把表表示成这种形式。
例如,例II(本书第77页)以格局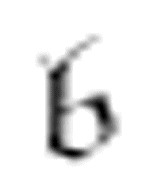 开始:
开始:
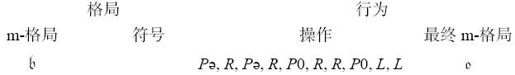
要想遵循图灵最初的(和恢复后的)约定,这一格局必须分成六个简单的格局。对于其他格局,我将使用德语小写字母c、d、e、g和h(f在原始表中已经使用过)表示。

现在,每个操作都只包含一个打印操作(或没有)和紧跟着的一个可能左移一格或右移一格的操作。
Now let us give numbers to the m-configurations, calling them q1, …, qR, as in §1. The initial m-configuration is always to be called q1.
现在我们给这些m-格局编号,正如§1中分别把它们称作q1,q2,…,qR。初始m-格局总是q1。
如果一台机器刚好有237种不同的m-格局,则将它们标记为q1到q237。
修改例II的开头,前六个m-格局分别重命名为q1到q6。图灵常用的初始m-格局的符号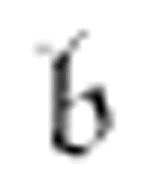 变成了q1。现在的表如下所示。
变成了q1。现在的表如下所示。
| 格局 | 行为 | ||
| m-格局 | 符号 | 操作 | 最终m-格局 |
| q1 | Pә, R | q2 | |
| q2 | Pә, R | q3 | |
| q3 | P0, R | q4 | |
| q4 | R | q5 | |
| q5 | P0, L | q6 | |
| q6 | L | q7 |
We also give numbers to the symbols S1, …, Sm
[240]
and, in particular, blank=S0, 0=S1, 1=S2.
我们也为符号S1,…,Sm编号,特别是,空=S0,0=S1,1=S2。
符号下标为1表示的是0,符号下标为2表示的是1,这种方法虽然有点令人困惑,但是我们必须适应它。例II中的机器也需要打印ә和x,因此需要为这台机器定义下面的等价关系。
S0代表空,
S1代表0,
S2代表1,
S3代表ә,
S4代表x。
计算2的平方根的机器需要从S0到S14的符号。
例II中机器的前六个格局现在如下所示。
| 格局 | 行为 | ||
| m-格局 | 符号 | 操作 | 最终m-格局 |
| q1 | PS3, R | q2 | |
| q2 | PS3, R | q3 | |
| q3 | PS1, R | q4 | |
| q4 | R | q5 | |
| q5 | PS1, L | q6 | |
| q6 | L | q7 |
The lines of the table are now of form
| m-config. | Symbol | Operations | Final m-config. | |
| qi | S j | PS k, L | q m | (N1 ) |
| qi | S j | PS k, R | q m | (N2 ) |
| qi | S j | PSk | q m | (N3 ) |
现在表中各行的形式如下:
| m-格局 | 符号 | 操作 | 最终m-格局 | |
| q i | S j | PS k, L | q m | (N1 ) |
| q i | S j | PS k, R | q m | (N2 ) |
| q i | S j | PS k | q m | (N3 ) |
规定使用统一的命名系统使得这些行都拥有非常相似的模式。图灵区分了一般情形下的三种不同的标准形式。
在最右端,图灵把这三种标准形式记作N1、N2和N3。这三种形式都会打印一些字符,不同之处在于读写头是移至左边、右边或是不动。
擦除操作呢?因为图灵使用S0来表示一个空的符号,所以擦除操作可以只通过简单地打印S0来完成。
Lines such as
| q i | S j | E, R | q m |
are to be written as
| q i | S j | PS0, R | q m |
如下这样的行:
| q i | S j | E, R | q m |
可以写成:
| q i | S j | PS0, R | q m |
不打印任何符号的右移或者左移操作,可以写成重新打印扫描符:
and lines such as
| q i | S j | R | q m |
to be written as
| q i | S j | PS j, R | q m |
In this way we reduce each line of the table to a line of one of the forms (N1), (N2), (N3).
而如下这样的行:
| q i | S j | R | q m |
可以写成:
| q i | S j | PS j, R | q m |
通过采用这种方法,我们可以把表的每一行都简化为(N1)、(N2)或(N3)三种形式中的一种。
我一直用例II表中的第一个格局来阐明标准化表的过程,但是这个格局的符号列什么都没有,因为这个格局所做的操作与符号无关。由于一台机器以一个空白纸带开始,因此它读取的符号是一个空白。将例II中的第一个格局转换成标准形式后,结果如下:
| 格局 | 行为 | ||
| m-格局 | 符号 | 操作 | 最终m-格局 |
| q1 | S0 | PS3, R | q2 |
| q2 | S0 | PS3, R | q3 |
| q3 | S0 | PS1, R | q4 |
| q4 | S0 | PS0, R | q5 |
| q5 | S0 | PS1, L | q6 |
| q6 | S0 | PS0, L | q7 |
这个相当简单。我们来看看例II机器中的第二个m-格局:
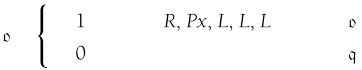
这个m-格局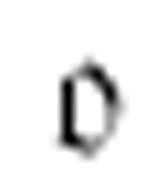 编号后表示成q7。当扫描到的字符是1时,读写头向右移动一次,然后向左移动三次。这样的三次左移需要另外三个m-格局q8、q9和q10。m-格局将
编号后表示成q7。当扫描到的字符是1时,读写头向右移动一次,然后向左移动三次。这样的三次左移需要另外三个m-格局q8、q9和q10。m-格局将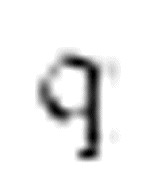 变成q11。m-格局q7如下:
变成q11。m-格局q7如下:
| 格局 | 行为 | ||
| m-格局 | 符号 | 操作 | 最终m-格局 |
| q7 | S2 | PS2, R | q8 |
| q7 | S1 | PS1 | q11 |
在这两种情况下,机器都打印扫描到的字符。m-格局q8、q9和q10如下:
| q8 | S0 | PS4, L | q9 |
| q9 | S2 | PS2, L | q10 |
| q10 | S0 | PS0, L | q7 |
问题出自符号列。你需要知道机器接下来会遇到哪个字符,才能保证正确填写该列。对于q8,机器扫描到一个空格,然后打印一个x。一旦它向左移动,接下来被扫描到的是哪个字符呢?它应该是刚才在q7里扫描的那个1,但是在其他情况下,结果可能不会如此明显。”任一”、”否”或者”其他”在这个模式下都不起作用,在某些情况下,你可能不得不为机器使用的每一个单独的字符添加特定的格局。
这样的确有点乱,但是我们总是只涉及有限个字符,因此这些操作一定可以完成。假设我们已经将某台机器的所有格局都转换成了图灵记作(N1)、(N2)和(N3)的标准形式。当完成转换时,我们会丢掉原始的表,这样会丢失任何信息吗?是的,确实丢失了一点信息。我们知道S0是空,S1是0,S2是1,但是我们不再知道S3、S4等代表的准确字符是什么。这个应该没有关系。机器在内部使用这些字符。要紧的是它们必须是唯一的。我们真正关心的只是机器打印的0和1的数字串,而不关心它使用什么作为缓存记号。
我们可以不使用表,而用m-格局、符号、L和R的组合来表示每个格局。
From each line of form (N1) let us form an expression qiSjSkLqm;
对于形式为(N1)的每行,我们使用表达式qiSjSkLqm。
这种形式有时被称作五元组,因为它是由五个元素组成的。尽管这样表达让人感觉很神秘,但它仍然是可读的:“在m-格局qi中,当扫描到字符Sj时,打印字符Sk,然后向左移,最后转向m-格局qm”。对于N2和N3形式的写法是相似的。
from each line of form (N2) we form an expression qiSjSkRqm; and from each line of form (N3) we form an expression qiSjSkNqm.
形式为N2的每行都可以表示为qiSjSkRqm,N3则表示为qiSjSkNqm。
注意,如果读写头不移动,那么对应的字母将是N(意思是不移动)。
Let us write down all expressions so formed from the table for the machine and separate them by semi-colons. In this way we obtain a complete description of the machine.
我们把机器表中这样形成的表达式写下来,并且用分号分隔开来。如此一来,我们就得到机器的完整描述。
图灵很快会给出一个例子。每个格局都是一个五元组,一个完整的机器就被表示成一连串的五元组。(有趣的是,这些五元组不必按照某个特定的顺序排列。就像在程序语言中,每个语句以标签开始,以goto语句结束。)
下面进行的替换是彻底的替换。它去掉了所有下标,把机器转换成了一连串的大写字母。
In this description we shall replace qi by the letter “D” followed by the letter “A” repeated i times, and Sj by “D” followed by “C” repeated j times.
在下面的描述里,我们将用D和后面i个字母A来代替qi ,用D和后面j个字母C表示Sj。
比如,q1 可以由DA代替,q5 由DAAAAA代替(记住,第一个格局是q1,没有q0)。对于符号,S0(空)表示成D,S1(符号0)表示成DC,S2(符号1)表示成DCC,S3表示成DCCC,以此类推。
This new description of the machine may be called the standard description (S.D). It is made up entirely from the letters “A”, “C”, “D”, “L”, “R”, “N”, and from “;”.
这种新的机器描述方法称为标准描述(S.D)。它完全是由字母A、C、D、L、R、N和分号“;”组成的。
其中,L、R和N表示读写头的移动。分号用来分隔每个格局。
If finally we replace “A” by “1”, “C” by “2”, “D” by “3”, “L” by “4”, “R” by “5”, “N” by “6”, and “;” by “7” we shall have a description of the machine in the form of an arabic numeral.
如果最后用1代替A,2代替C,3代替D,4代替L,5代替R,6代替N,7代替”;”,我们将得到阿拉伯数字形式的机器描述。
这是很重要的一步。图灵已经把他的机器标准化到了可以用一个整数来唯一确定一台机器,这一整数将机器的所有状态进行了编码。哥德尔曾在他的不完备性定理中将每个数学表达式转化成唯一的数字,图灵无疑在此受到了哥德尔方法的启发。
The integer represented by this numeral may be called a description number (D.N) of the machine. The D.N determine the S.D and the structure of the
[241]
machine uniquely. The machine whose D.N is n may be described as(n).
由这些数字表示的整数可以称作机器的描述数(D.N)。D.N唯一决定了S.D以及机器的结构。
D.N为n的机器可以描述为(n)。
图灵又引入了另一种字体。他将使用这种手写字体来表示整台机器。
To each computable sequence there corresponds at least one description number, while to no description number does there correspond more than one computable sequence.
每个可计算序列至少对应一个描述数,但不存在一个描述数对应多个可计算序列。
由于五元组的序列无关紧要,因而打乱这些五元组的顺序,不会影响机器计算出的序列。很明显,可以有多个描述数与一个可计算序列相关,但是每个描述数都定义了一台只能产生一个可计算序列(至少在以一个空白纸带开始的情况下)的机器。
不知不觉地,图灵就得到了他在论文开始提到的一个结果:
The computable sequences and numbers are therefore enumerable.
因此,可计算序列和可计算数是可数的。
你可以通过列出所有可能的描述数来枚举可计算序列,因为描述数其实就是整数。图灵没有陈述的一点是,可计算数只是实数一个可数的子集。因为可计算数是可数的,而实数是不可数的,所以存在很多不可计算的实数。这一主题将在后面更多地探讨。
Let us find a description number for the machine I of §3.
我们来寻找§3中机器I的描述数。
最初,那台机器是由如下表定义:

When we rename the m-configurations its table becomes:
| q1 | S0 | PS1,R | q2 |
| q2 | S0 | PS0,R | q3 |
| q3 | S0 | PS2,R | q4 |
| q4 | S0 | PS0,R | q1 |
重命名这些m-格局之后,表变成:
| q1 | S0 | PS1,R | q2 |
| q2 | S0 | PS0,R | q3 |
| q3 | S0 | PS2,R | q4 |
| q4 | S0 | PS0,R | q1 |
这是一种很直接的转换。
Other tables could be obtained by adding irrelevant lines such as
| q1 | S1 | PS1,R | q2 |
通过增加如下的无关行可以得到其他表:
| q1 | S1 | PS1,R | q2 |
也就是说,增加一些不起作用的行可以得到生成相同可计算序列的其他表。如果机器开始时纸带是空白的,并且每当打印一格后它总是向右移动,那么机器将永远扫描不到数字0。
Our first standard form would be
q1 S0 S1 R q2; q2 S0 S0 R q3; q3 S0 S2 R q4; q4 S0 S0 R q1;.
我们得到的第一个标准形式如下:
q1S0S1Rq2; q2S0S0Rq3; q3S0S2Rq4; q4S0S0Rq1;.
这一标准形式是通过取表中的四行,并用分号将这四行代表的格局分开得到的。把它转化成标准描述,要求将qi替换成D与i(1个或更多)个A相连的序列,将Sj替换成D与j(0个或更多)个C相连的序列。
The standard description is
DADDCRDAA;DAADDRDAAA;
DAAADDCCRDAAAA;DAAAADDRDA;
标准描述为:
DADDCRDAA;DAADDRDAAA;
DAAADDCCRDAAAA;DAAAADDRDA;
标准描述很难阅读,但是经常使用,因此你应该努力去熟悉它。为了把它解码成其原来的组成部分,我们先来关注每一个D。每个D都代表了一个格局或者一个符号。
⟩ 如果这个D后紧跟若干个A,那么它代表了一个格局。这个格局编号是A的数目。
⟩ 如果D后不是A,那么它是一个符号。这种情况下,D后跟随的是0个或更多个C。如果只是D本身,那么它表示一个空格;否则,DC表示0,DCC表示1,与更多的C相连表示其他符号。
图灵更多使用的是标准描述,而不是描述数。描述数更多地存在于抽象意义上,图灵不对这些数字进行任何计算。在他所展示的例子中,你可以用1代替A,用2代替C,用3代替D,用5代替R,用7代替分号,来得到一个描述数。
A description number is
31332531173113353111731113322531111731111335317
and so is
3133253117311335311173111332253111173111133531731323253117
一个描述数是:31332531173113353111731113322531111731111335317, 而3133253117311335311173111332253111173111133531731323253117也是一个描述数。
第二个数除了尾部增加了一些数字(31323253117)之外,和第一个数是一样的,这些增加的数字对应了图灵定义的”不相关的”格局q1S1S1Rq2。问题在于:这两个数定义了两台不同的机器,而这两台机器又计算得到两个完全相同的数。回想一下,这个数是1/3的二进制形式。也就是说,一台机器的格局重组后仍然可以计算产生相同的数,但是它们的描述数是不同的。
这个数太大了!显然,图灵并不在意这些数有多大。例如,为了表示出q35,他或许能想出一种办法把35放进描述数中,但是他没有这么做。为表示q35,标准描述要使用如下序列:
