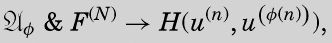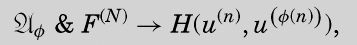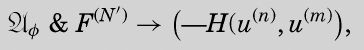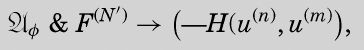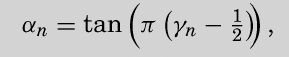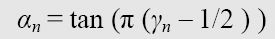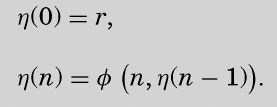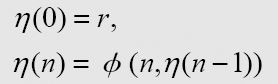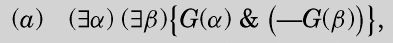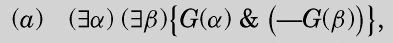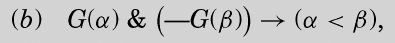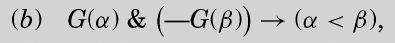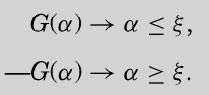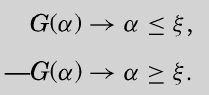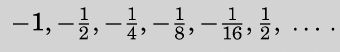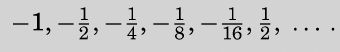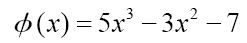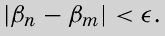第13章

可计算函数

你上一次使用个人计算机计算无理数的无穷数位是在什么时候？除非你是通过运行程序计算你的数百万位数字来消遣，否则你采用的任何程序计算出的数位都不可能超出你喜爱的计算器的计算范围。

很显然，图灵在他的论文中建立了很多计算机编程的原理和概念，但是无论是在以前、现在或是将来，计算实数的无穷数位都必然不是计算机的典型活动。

实际上，计算机执行的是已经被程序员分割成若干组块的任务，这些块称作函数、例程、子程序或方法（称呼取决于特定的编程语言）。一般来说，这些函数在有限的时间段内执行某个特定的任务，它们从接收输入开始，然后对这些输入进行数学运算以产生输出，最后把控制转移给其他函数。

函数的概念起源于数学。概括地说，函数是把输入转换成输出的数学实体。输入称作函数的参数或自变量；输出称作函数的值或因变量。函数通常被限制在特定类型的数字或其他对象上。合法的输入称作函数的定义域，所有可能的结果输出值称作值域。

图灵在其论文的第一段提到了“可计算函数”的概念，并把它作为未来探索的主题：

尽管本论文的主题是可计算数，但是我们同样可以容易地定义和研究可计算函数，其变量可以是整数、实数、可计算数、可计算谓词等。……我希望可以很快就给出可计算数、函数等之间的关系，这将包括对用可计算数表示的实变函数理论的研究。

图灵并没有严格按这种方法深入研究这些主题。你在第17章会看到，当斯蒂芬·克莱尼（在他于1952年出版的《数学引论》中）和马丁·戴维斯（在他于1958年出版的《可计算性与不可解性》中）重新设计了图灵机并用它们来计算整数函数而不是实数时，可计算函数的概念就变得十分重要了。

在某种意义上，我们已经看到了执行函数的机器。通用机就是这样的，因为它把机器的标准描述作为输入，输出中包括该机器的完全格局以及机器本应计算的序列。

更传统的函数呢？它们是什么样子的？想想三角正弦函数。输入是一个表示角度的数值，通常以度或弧度为单位。假定这个角是直角三角形中的一个角，则正弦函数计算该角的对边与斜边的比。更一般地说（定义大于90°的角的正弦函数），从笛卡儿坐标系的原点出发到任意一点画一条线。这条线与X轴的夹角（按逆时针方向测量）的正弦函数值，就是这条线的端点到X轴的距离与该直线长度的比值。

尽管正弦函数是以360°或2π个弧度为周期循环的，但是该函数的定义域由所有实数组成，它的值域（函数的值）由从-1到1之间的实数（包括-1和1）组成。

实际计算正弦函数是要用到如下的无穷级数，其中x以弧度为单位：

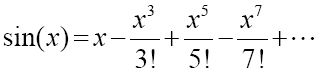
这就是如今的计算机计算正弦函数时所用的公式，尽管一般情况下，这种计算是在计算机的处理芯片而非软件中进行的。

因为实数拥有无穷数目的十进制位，因此计算机不能存储任意的实数，而是用有理数来近似实数。1985年，美国电气和电子工程师协会（IEEE）公布了二进制浮点运算的IEEE标准，很多计算机系统都使用该标准，以一种适合于科学计数法表示的形式存储数字。例如，常用的双精度格式使用64位存储一个数：1位用来存储符号（正或负），11位用来存储指数，52位用来存储尾数，提供大致相当于16位十进制数的精度。^［1］实质上，我们是用两个整数来存储实数123.456的，它们分别是8 687 443 681 197 687（尾数）和46（指数），因为8 687 443 681 197 687除以2⁴⁶近似等于123.456。这个比值是一个有理数，而不是实数。

当计算机计算一个正弦值时，这一近似是很重要的，因为它可以保证函数在有限时间内完成。尽管正弦函数是作为一个无穷级数来计算的，但是这个级数项的绝对值越来越小。当项对结果的精度不再产生影响时，函数就终止了。

然而，图灵机追求无限的精度。计算实数时，它会一直不停地运算。由于计算正弦函数的无限级数中的每个项都包含无限的位数，因此在计算正弦函数时，追求无限的精度是个大问题。例如，当角度是1弧度时，第二项是1/6，无论表示成十进制还是二进制，它都需要无限位数。如果机器需要计算第二项的无限个数位，它怎么样才能运行到对第三项的计算呢？

一种可行的方法是，依次计算每一项的第一位，直到某一项的第一位数字为0，然后，再依次计算每一项的第二位，直到某一项的前两位数字均为0，依此类推。这显然是一个很复杂的过程，特别是你不想机器在计算得到结果后再擦除结果的任意位时。

执行正弦函数只是一个问题，输入从哪里来呢？

或许我们的直觉是让机器的使用者以某种方式“键入”机器需要计算的角。这显然是受现在的交互式计算机和屏幕计算器的启发，但是为了接受这种形式的输入，需要重新设计图灵机。这比目前我们所做的工作量更大。

第二种观点是将函数的输入“硬编码”在机器内部。例如，我们可以设计一台专门计算37.85°的正弦值的机器。尽管这样会把机器限制为只能求解某一个角度的正弦值，但是我们还是希望设计出的这种机器易于修改，从而可以计算其他角度的正弦值。

第三种方法是把角度编码到纸带上。机器读取这个输入，计算正弦值，然后再把结果打印到纸带上。（我猜你喜欢这么做！我也是。）

第四种方法是让机器自己产生输入。例如，机器首先计算角度为0°的正弦值，然后计算角度为1°的正弦值，再计算角度为2°的正弦值，等等，并把每个结果都打印在纸带上，最后会得到一张包含很多角度正弦值的“表”。这种方法要求机器计算得到的每个结果都只包含有限个数位。

第五种方法需要两台不同的机器。第一台机器计算实数，第二台计算该数的正弦值。我说两台机器的时候，实际上是指可以实现两台机器逻辑的一台机器。我们已经遇到过以这种方式结合的机器。在第8节中（本书第166～167页），图灵把一台判定机器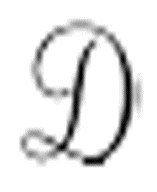和通用机结合起来，构造成机器来分析标准描述。这种做法的好处是，我们可以“插入”不同的第一台机器来计算不同角度的正弦值。

这些做法都是有问题的。一个大问题是正弦函数的输入和输出都是实数（至少理论上是这样的），而实数包含无限位。键入一个有无限位的数或将这样的数编码在纸带上都是不可能的。

事实上，即使你将角度限制在简单的、可以表示成有限的十进制数的范围内，正弦函数需要的也是弧度制的角度。180°对应对π个弧度，因此看上去很简单的10°其实是其π/18个弧度——一个包含无限个十进制位数的超越数。

现在我们面临的是一台需要计算现π/18弧度的机器和另一台计算该弧度的正弦值的机器，事实上这两台机器是在同一个“元机器”中运行的。第二台机器不可能等到第一台机器计算完成后再开始计算！这两台机器需要以串联模式工作，也就是有时称作“燕尾连接”的一种编程技术。计算角的机器得到一个新的数位时，计算该角度正弦值的机器必须接收这个数位，并计算出结果的一个新的数位。这两台机器间会永远进行这一相互作用的来回。

现在，你可能就不会对斯蒂芬·克莱尼和马丁·戴维斯重新改造的图灵机只能计算数论函数，也就是域和值域都限制在非负整数的函数，感到惊讶了。他们都把函数输入编码成笔画。例如，在8个连续的格中画简单的竖线来表示数字7（数字0只需要1画）。

通常情况下，当计算一个函数时，你不会想让这个计算永久进行下去。你希望函数会结束，这样便可以检测结果。因此，经克莱尼和戴维斯改造的图灵机在计算结束的时候会停止运行。显然，用于计算非负整数的加法和乘法的机器不需要永久地运行。在克莱尼和戴维斯的设计中，不能停止运行的机器被看作是故障机器。戴维斯把判定一台图灵机是否能够正确地完成计算并停机的过程称为停机问题。后来，停机问题被等同于图灵机，但是这个概念与图灵最初的论文无关。

既然我们已经考虑了构造处理实数函数的图灵机时遇到的一些与生俱来的问题，接下来我们准备学习图灵在他论文的第10节中提出的解决方法。

第10节其实是第9节的延续。前一节的开头，图灵对于其机器的计算能力问题给出了三个论据。第三个是第10节的主题，即“给出一大类可计算数的示例”。同时，图灵讨论的重点稍有改变，从原来的可计算数转移到了可计算函数的范围。

第10节可能是图灵论文中最少被分析的部分，通常也是最难理解的一节。他写得很简洁，有时还有点模糊。我没有信心总是能够完全准确地揭示他的论点。

也许这并不令人惊讶，图灵一开始就讨论了“带有整数变量的可计算函数”，并且定义这样函数的“最简单的”方式需要非负整数的定义域和值域。

10. Examples of large classes of numbers which are computable.

It will be useful to begin with definitions of a computable function of an integral variable and of a computable variable, etc. There are many equivalent ways of defining a computable function of an integral variable. The simplest is, possibly, as follows. If γ is a computable sequence in which 0 appears infinitely^† often, and n is an integer, then let us define ξ(γ,n) to be the number of figures 1 between the n-th and the (n + 1)-th figure 0 in γ. Then ø(n) is computable if, for all n and come γ, ø(n) = ξ(γ,n).

^† If computes γ, then the problem whether prints 0 infinitely often is of the same character as the problem whether is circle-free.

10. 大量可计算数的示例

以定义整数变量和可计算变量的可计算函数开始，会非常有用。有很多等价的方法用来定义整数变量的可计算函数。下面的定义可能是最简单的。如果γ是一个可计算序列，其中0出现无穷次^†，n是一个整数，我们定义ξ(γ, n)为γ中第n个0和第(n+1)个0之间数字1的个数。如果对于所有的n，存在某个γ，使得ø(n) = ξ(γ, n)，则ø(n)是可计算的。

^† 如果计算γ，则是否无限打印0的问题与是否是非循环的问题是同一性质。

我需要举例子说明。假设函数ø（希腊字母phi）简单定义为：

ø(n) = 2n + 1，

其中n为非负整数。则，

ø(0) = 1

ø(1) = 3

ø(2) = 5

ø(3) = 7

…

对应于该函数的序列γ（希腊字母gamma）为：

010111011111011111110…

注意，两个相邻的0之间分别是一个1、三个1、五个1、七个1等，1的数目与每个连续的非负整数n的函数ø(n)的值相对应。

γ是可计算序列吗？对我而言，它的确看上去是可计算的。这意味着ø(n)是一个可计算函数，计算γ的机器永远不停地运行，计算出函数所有的值。

图灵从与我的例子完全相反的角度处理这个可计算函数的问题：他假定γ序列总是包含无穷个0，函数 ξ(γ, n)（希腊字母xi）表示每对相邻的0之间数字1的个数，并且 ø(n)=ξ(γ, n)。

从这点看，计算包含无穷个0的序列的任何机器也是在计算一个正整数值的函数，尽管一般情况下，我们不能判定机器是否确实满足这个标准。

现在，图灵假定一个与函数ø相对应的谓词，使得该函数的计算类似于数字的基于逻辑的演算，也就是图灵在论文第9节、本书前一章中论述的内容。

An equivalent definition is this. Let H(x, y) mean ø(x)=y.

如此，我们得到一种等价的定义。定义H(x, y)，其中ø(x) = y。

我们使用相同的例子。改变函数的自变量，现在的定义如下：

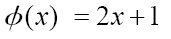
使用前一章中描述的谓词I来定义H(x, y)：

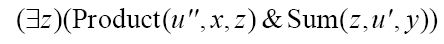
如果存在某个z，使得2乘以x等于z，且z加1等于y均为真，则该公式为真。

Then, if we can find a contradiction-free axio, such that φ→P,

然后，如果我们能找到一个非矛盾的公理_ø，使得_ø → P，

则ø一定是定义H所需谓词的公理（这个例子中的Product和Sum）与P的合取式，因此这个蕴涵式很容易就成立。

and if for each integer n there exists an integer N, such that

并且如果对每个整数n都存在一个整数N，使得

你会想起，F⁽ⁿ⁾是后继函数的合取式的缩写形式。N必须至少等于n和ø(n)中较大的一个。在我们的例子中，当n = 10时，ø(n)=21。函数H内部需要数字1和2，并且z的值为20。因此，N必须至少等于21才能定义足够多的数字，而在某些情况下，它可以比n和ø(n)的值都大。

and such that, if m≠ø(n), then, for some N′,

且使得如果m≠ø(n)，则对某个N’，

公式末尾漏掉了右半括号。总之，当第一个参数为n，第二个参数为ø(n)时，谓词H为真，否则为假。对于第二个公式，N’的值也至少要等于m，但是稍后你将看到，我们在演示中不会涉及比n大的m值。

then ø may be said to be a computable function.

则可以说ø是一个可计算函数。

到这儿，图灵结束了他的讨论，但并没有真正描述它应该如何发挥作用。机器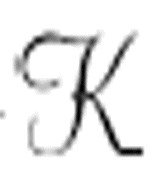的另一种修正，是枚举出所有可证明的公式。图灵在第9节描述的机器针对n的连续取值依次枚举出这些可证明的公式，根据谓词G的真值，为n的每个值打印一个0或1。

这里的新问题需要一台机器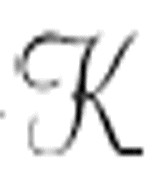_γ来计算前面描述的序列γ：

010111011111011111110…

其中，每个1串中数字“1”的数目为对应于n的连续值的函数ø(n)的值。最大的不同是，这台机器不仅对连续的n值，还对变化的n和m的值，枚举出所有可证明的公式。

对于n和m的每个新值，机器首先打印公式A和B（仍使用为之前的机器设置的术语）：

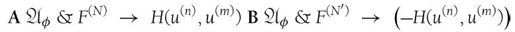
然后通过产生所有的可证明的公式，尝试与二者中的一个进行匹配。

机器从n等于0开始计算。n是函数ø(n)的参数，也是谓词H(n, m)的第一个参数。对n的每个新的值，机器打印一个0，然后把m设置为0。m可能是函数ø(n)的结果，它是谓词H(n, m)的第二个参数。

对m的每个新的取值，机器开始产生所有可证明的公式。如果与公式B匹配，则机器打印一个1，因为m的值不是函数ø(n)的结果。机器增大m，打印新的A和B，然后再次开始产生可证明的公式。如果与公式A匹配，则该m值是函数ø(n)的结果，机器继续对n的下一个值进行处理。对于n的下一个值，机器开始打印一个0，并且将m设置回0。

以这种方式，机器打印出序列γ，其中的每个1串中数字1的数目都表示依次增大的整数参数对应的函数值。

We cannot define general computable functions of a real variable, since there is no general method of describing a real number,

由于没有描述实数的一般方法，因而我们无法定义一般的实数变量的可计算函数。

这就是我之前考虑将实数编码在纸带上供函数处理时遇到的问题。

but we can define a computable function of a computable variable.

但是，我们可以定义一个以可计算数为变量的可计算函数。

这需要可计算数的计算和可计算函数的计算串联工作。在或许是最简单的情况下，每次计算得到变量的一个新数位后，可计算函数就会接收它，并打印出结果的新的数位。可计算变量和可计算函数始终保持相同的有效数位，从而保持相同的精度。

图灵所采用的例子是三角正切函数。他想对各种各样的，其实是所有的可计算数计算它们的正切值，但是他没有为一个计算的终止和另一个计算的启动指定任何标准。

If n is satisfactory, let γ_n be the number computed by (n), and let

[255]

unless γ_n = 0 or γ_n = 1, in either of which cases α_n = 0.

如果n是可接受的，假定γ_n为机器(n)计算得到的数字，并且

除非γ_n＝0或者γ_n＝1。在这两种情况下，α_n＝0。

后面的脚注表明这不是唯一可能的函数，不过图灵特地挑选了一个简单的例子。因为图灵机计算0和1之间的实数，所以无论机器如何定义，γ_n的值都介于0和1之间。正切函数的参数范围介于之1/2π和1/2π之间，这是用弧度制表示的角，等价的角度范围是之-90°到90°。

Then, as n runs through the satisfactory numbers, α_n runs through the computable numbers^†.

^† A function α_n may be defined in many other ways so as to run through the computable numbers.

接着，随着n遍历可接受数，α_n遍历可计算数^†。

^† 函数α_n也可以用许多其他方式来定义，从而能够遍历可计算数。

-90°到90°之间角度的正切值的变化范围是（–∞, ∞），因此它覆盖了整个实数集。（严格地说，）-90°和90°角的正切值没有定义，这也正是为什么图灵单独处理这两种情况的原因。）除去极少数例外，正切函数的结果都是超越数。

图灵后来才建议，我们事实上可以定义计算一个角的正切值的图灵机。跟正弦函数相似，正切函数也可以通过一个无穷级数来计算：

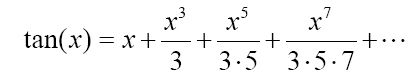
x的变化范围从围1/2π到1/2π。

Now let ø(n) be a computable function which can be shown to be such that for any satisfactory argument its value is satisfactory^‡. Then the function f, defined by f(α_n)=α_ø(n), is a computable function and all computable functions of a computable variable are expressible in this form.

^‡ Although it is not possible to find a general process for determining whether a given number is satisfactory, it is often possible to show that certain classes of numbers are satisfactory.

令ø(n)为一个可计算函数，对任意的可接受参数，它的值都是可接受的^†。则定义为f(α_n)=α_ø(n)的函数f是一个可计算函数，并且所有可计算变量的可计算函数都可以表示成这种形式。

^† 尽管不可能找到可以判定某个给定的数字是否是可接受的通用过程，但是通常情况下，表明某一特定类的数字是可接受的还是有可能的。

函数ø(n)的定义域和值域都是符合要求的机器的描述数。或许我们只考虑某种特定格式的机器，很容易就可以将其构造成是符合要求的。函数ø(n)修改描述数，其实是重新编程机器，使得它可以计算出其他东西。例如，ø(n)可以重新编程机器，使它不再求解x，而是x的两倍再加1，即执行函数2x + 1。

Similar definitions may be given of computable functions of several variables, computable-valued functions of an integral variable, etc.

I shall enunciate a number of theorems about computability, but I shall prove only (ii) and a theorem similar to (iii).

类似地，也可以定义包含几个变量的可计算函数、包含整数变量且值为可计算数的函数，等等。

我将给出一些关于可计算性的定理，但是只证明(ii)及与(iii)相似的定理。

随后的十个定理用小写罗马数字编号。图灵论文第10节的最后两页给出了对(ii)和(iii)的证明。

(i) A computable function of a computable function of an integral or computable variable is computable.

(i) 以整数或可计算数为变量的可计算函数的可计算函数是可计算的。

换句话说，我们可以把这些东西堆积起来。从计算一个数的机器出发，使用另一台机器执行这个数的函数，然后再使用一台机器执行第一个函数的结果的函数。与之前基于三角正切函数的机器类似，这些机器不会等待前一阶段完成以后再运行。它们必须以串联方式工作，或许是随着每一个数位的计算，从一个阶段向另一个阶段传递信息。

(ii) Any function of an integral variable defined recursively in terms of computable functions is cpmputable. I.e. if ø(m,n) is computable, and r is some integer, then η(n) is computable, where

(ii)以可计算函数递归定义的任何包含整数变量的函数是可计算的。例如，如果ø(m, n)是可计算的，r是整数，则η(n)是可计算的，其中，

注意，希腊字母η（读为eta）与斜体的n有点相像。“包含整数变量的函数”是η，“可计算函数”指的是ø(m, n)。作为例子，我们假设r = 1，函数ø(m, n)简单定义为：

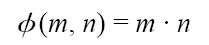
我确定ø(m, n)是可计算的。我们计算η的几个值：

η(0) = r = 1

η(1) = ø(1, η(0)) =ø(1, 1) = 1·1 = 1

η(2) = ø(2, η(1)) =ø(2, 1) = 2·1 = 2

η(3) = ø(3, η(2)) =ø(3, 2) = 3·2 = 6

η(4) = ø(4, η(3)) =ø(4, 6) = 4·6 = 24

η(5) = ø(5, η(4)) =ø(5, 24) = 5·24 = 120

…

函数η(n)是阶乘函数的递归定义。到本节最后，图灵将证明使用可计算函数ø(m, n)定义的整数函数（如 η(n）本身也是可计算的。

(iii) If ø(m, n) is a computable function of two integral variables, then ø(n, n) is a computable function of n.

(iii) 如果 ø(m, n)是一个包含两个整数变量的可计算函数，则ø(n, n)是关于的可计算函数。

这个定理听起来很平凡，但图灵利用这个机会做了一些有趣的事。本章以对它的证明结束。

(iv) If ø(n) is a computable function whose value is always 0 or 1, then the sequence whose n-th figure is ø(n) is computable.

(iv) 如果ø(n)是一个其值总为0或1的可计算函数，那么第n位数字为ø(n)的序列是可计算的。

例如，假设函数IsPrime(n)当n是素数时返回1，否则返回0。图灵断定下面的序列是可计算的：

0011010100010100010100010000010…

我只展示了n从0开始的前31位数字。与素数2、3、5、7、11、13、17、19、23和29对应的数位都设置成1。

图灵接着引用了戴德金定理。这里给出了G. H. 哈代的《纯数学教程》第1章中对该定理的陈述。1931年，图灵为准备剑桥大学的秋季入学考试开始阅读这本书，那也可能是他第一次遇到这个定理。

戴德金定理 如果按照以下的方法把实数集合分割成两类L和R：

(i) 每个数只属于两个类中的一类；

(ii) 每个类至少包含一个数；

(iii) L中的任意一个数都小于R中的任意一个数。

则存在一个数α，满足小于它的所有数都属于L类，大于它的所有数都属于R类。数α本身可能属于L或R中的任意一类。^［2］

第一次看到这个定理时容易感到迷惑，但是它描述了有理数和实数之间最基本的区别，特别是，实数是如何组成了连续统，而有理数不能。

想象从左边的负无穷到右边的正无穷有一条数轴，也可以只考虑这个数轴的一段。把它分割成两个部分（这称为戴德金分割）。一些数在左边的线上（定理中的L），另一些数在右边的线上（R）。

例如，你可以在1.5处分割这条直线，因此L中的所有数都小于1.5，R中的所有数都大于1.5。那1.5自身呢？你可以把它放在L中，也可以放在R中。把1.5放在L中，它是L中的最大数，R中没有最小数。换句话说，R中没有一个比其余的数字都小的数。另一方面，把1.5放在R中，它是R中的最小数，L中没有最大数。

在2的平方根处分割这条直线。如果这条数轴仅由有理数组成，那么L中的所有数都小于2的平方根，R中的所有数都大于2的平方根。因为2的平方根不是有理数，它既不属于L，也不属于R。此外，L中没有最大数，R中也没有最小数。这条直线在2的平方根处出现间断。

然而，如果这条数轴是由实数组成的，则2的平方根必须属于L或者R。你无法定义一个实数的分割，使得这个分割点既不属于L也不属于R。这就是为什么实数可以组成连续统，而有理数不能的原因。

Dedekind's theorem does not hold in the ordinary form if we replace “real” throughout by “computable”.

如果我们用“可计算数”替换“实数”，那么一般形式表示的戴德金定理就不成立了。

可计算数不能组成连续统，因为你可以在一个非可计算数处做戴德金分割。这个数也许太复杂（也就是太随机）而难以用算法定义，或者你也可以定义这个数，例如，由每个可计算数中的一个数位构成的数，但无法计算它。这个分割把可计算数分成两个部分，使得L中没有最大数，R中也没有最小数。

But it holds in the following form:

但是用下面的形式表示，戴德金定理仍然成立：

注意下面的罗马数字，这是在图灵定理(v)提出的。当参数（一个可计算数）小于（或者小于等于）某个固定数ξ（希腊字母xi）时，图灵在这里引入的命题函数G(α)为真。

函数G(α)把可计算数分成两类：L，使G(α)返回真的可计算数；R，使G(α)返回假的可计算数。哈代关于戴德金定理的描述满足条件(i)，因为对于每个可计算数，G(α)的值或为真或为假。

(v) If G(α) is a propositional function of the computable numbers and

(v) 如果G(α)是可计算数的命题函数，并且

图灵的公式(a)与哈代的条件(ii)等价，也就是每一类至少包含一个元素。

图灵的公式(b)与哈代的条件(iii)等价。如果G(α)为真，那么α在L中；如果G(β)为假，则β在R中，且α小于β。

and there is a geral process for determining the truth value of G(α), then [256] there is a computable number ξ such that

[256]

there is a computable number such that

并且存在判定G(α)真值的通用过程，那么存在一个可计算数 满足：

“判定G(α)真值的通用过程”的条件很重要。因为ξ是一个可计算数，一般情况下，它不能显式地存储在G(α)的定义中。然而，通过不断缩小这个值的范围，机器是有可能计算得到该数的。事实上，可以不断地检测G(α)的更加准确的值，计算ξ的机器就是这么做的。

In other words, the theorem holds for any section of the computables such that there is a general process for determining to which class a given number belongs.

换句话说，对于任意的可计算数，只要存在判定某个给定的数属于哪一类的通用过程，戴德金定理都是成立的。

在下一句话中，“可计算数序列”这个表达可能有点模糊，因为几乎从论文的开始，图灵都是使用“可计算序列”来指代机器产生的数位。他这里所说的“序列”指的是可计算数的有序集合。

Owing to this restriction of Dedekind's theorem, we cannot say that a computable bounded increasing sequence of computable numbers has a computable limit. This may possibly be understood by considering a sequence such as

由于戴德金定理的这个局限性，我们不能声称一个可计算的有界递增可计算数序列是有可计算的极限的。看看下面的序列或许有助理解：

几年前，sci.logic新闻组的讨论主题就是这一小段文字，http://sci.techarchive. net/Archive/sci.logic/2004-08/2244.html上记录了这一进程。一种见解是，最后的1/2是错误的，事实上应该是是1/32。修正后，这个序列好看多了，但是它不可能是图灵所想的，因为如果是这样，这个序列显然越来越接近于0，而0当然是一个可计算的极限。

一种貌似更加合理的推测是，图灵正在展示的序列看上去是趋向一个可计算的极限，但事实上并非如此。这个序列或许约束在一1和1之间，但是它并没有告诉我们这个极限是否真的可计算。

On the other hand, (v)enables us to prove

(vi) If α and β are computable and α < β and ø(α) < 0 < ø(β), where ø(α) is a computable increasing continuous function, then there is a unique computable number γ, satisfying α < γ < β and ø(γ) = 0.

另一方面，(v)使得我们可以证明：

(vi)如果α和β是可计算的，且α<β，ø(α)<0<ø(β)，其中，ø(α)是一个可计算的递增连续函数，那么存在唯一的可计算数γ满足α<γ<β，且ø(γ)=0。

图灵暗指一个可计算函数，它可能是一个多项式：

众所周知，任何奇数次（最大的指数）的实多项式都至少有一个实根，也就是说，有一个值x使得这个多项式的值为0。

对于多项式ø(x)，通过观察ø(1)=-5， ø(2)=21，可以缩小根的范围。这个根必须介于1和2之间。

数字1和2就是图灵描述中的α和β，你可以发现α < β且ø(α)<0<(β)。因为这个函数是连续的（即没有中断），所以存在一个值γ，它介于α和β之间，且ø(γ)的值为0。我们目标就是计算这个γ。我们可以在α和β的中间选择一个数，如1.5，计算ø(1.5)，结果为3.125。因为3.125大于0，所以可以把1.5作为新的β值。现在我们知道根是1和1.5之间的某个数。再尝试1.25。ø(1.25) = (1.921875，结果小于0，因此把1.25作为新的α值。现在我们知道这个根介于1.25和1.5之间。每一步都可以把这个根约束在一个更小的范围内，事实上就是在计算这个根。

粗略地说，如果一个数列中两个连续数的差的绝对值越来越小，那么我们称这个数列是收敛的。（我说“粗略地”是因为在序列的前面部分，这些差值的绝对值可能不会变小。）任何实数都可以表示成一个有理数的收敛序列。最简单地，可以使用如下的有理数序列来描述一个实数：

α₀ = 3

α₁ = 3.1

α₂ = 3.14

α₃ = 3,141

α₄ = 3,1415

α₅ = 3/14159

…

这些全是有理数，它们都越来越接近于无理数这。这个序列是收敛的，因为连续的两个数的差值越来越小，如a₃和a₄的差为0.0005，而a₄和a₅的差为0.00009。

数学上，常把这个差用一个小写的ε（读为epsilon）表示。你可以选择任意小的ε值，如0.0001。对于这个ε值，如果存在某个数N，使得对所有的n > N和m > N，对应项a_n和a_m的差的绝对值都小于我们所选的任意小的数，即，则该序列是收敛的。在上面的例子中，ε的值为0.0001，N为3，因为，当n和m大于3时，a_n和a_m的差也同样会小于0.0001。

图灵以类似的方式定义了可计算收敛。

Computable convergence.

We shall say that a sequence β_n of computable numbers converges computably if there is a computable integral valued function N(η) of the computable variable η, such that we can show that, if η > 0 and n > N(η) and m > N(η), then

可计算收敛

如果对于可计算变量ε存在一个可计算整数函数N(ε)，使得对于任意 那么我们称这个由可计算数组成的序列β_n为可计算收敛的。

在这里，序列中的数必须是可计算的，图灵还要求ε是可计算的，且N(ε)是可计算函数。