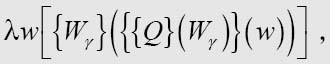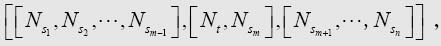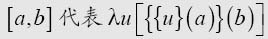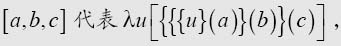where

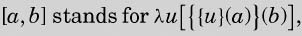
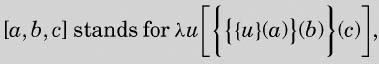
etc.

如果M_γ表示

那么它将具备所需要的性质。^†

^† 在可计算序列的λ可定义性的完整证明中，最好改变这个方法，用我们的机器能够很好处理的描述代替完全格局的数字描述。我们选择某些整数来代表这些符号和机器的m-格局。假设在特定的完全格局中，那些代表纸带上后续符号的数字是S₁S_2…S_n，其中第m个符号被扫描到，m-格局的标号为t，那么我们可以用下面的公式表示这个完全格局

其中

等等。

在图灵证明的第二部分，他开始自己寻找公式M_γ，使得对于所有n，

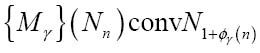
这个公式告诉我们序列的第n位是0还是1。我们先来分析：

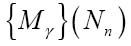
用图灵刚刚为M_γ推导出的公式代替之：

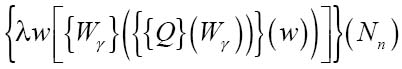
用N_n替代w：

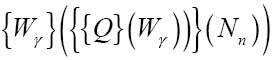
括号中的表达式可以转换为N_r(n)，因此

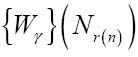
已经表明，这个公式可以转换为N₁、N₂或 N₃，这主要取决于完全格局r(n)打印的是0或1或其他。然而，r(n)定义了只有在完全格局打印了0和1的情况下才返回。

上面的脚注表明，完全格局在纸带上被分为了下一个扫描符之前部分及下一个扫描符之后部分。图灵所建议的用来表示纸带这些部分的λ表达式可以是非常长，并且大小会随着完全格局的增长而增长。

下面是论文的结尾。

The Graduate College,

Princeton University,

New Jersey , U.S.A.

研究生院，

普林斯顿大学，

美国新泽西州。

对于更加严格的证明，图灵并没有遵循他在这里概述的证明逆命题的思路。论文“可计算性和λ可定义性”于1937年9月11日被《符号逻辑杂志》收录，这时距他抵达普林斯顿还不到一年的时间。^［20］文章开始写道：

我们已经给出了许多定义用来表述与“有效计算性”的直观思路相对应的确切含义，并将其应用到了正整数函数中。这篇论文的意图是为了表明作者所介绍的可计算函数与邱奇发明的λ可定义的函数，以及与由赫尔布兰德和哥德尔引入并由克莱尼发展的一般递归函数是一致的。（在本论文中）已表明，任意的λ可定义函数都是可计算的，并且每一个可计算函数是一般递归函数。

图灵首先通过给出一台图灵机来证明λ可定义函数是可计算的。这台图灵机可能比图灵的通用机更复杂，它可以解析和转换λ函数。

证明的第二部分展示了可计算函数是递归的。图灵并不需要证明可计算函数是λ可定义的，因为斯蒂芬·克莱尼已经证明了递归函数是λ可定义的（在“λ可定义性和递归”一文中）。这样，有效计算性的三个定义被等价地联系起来了。

图灵后来经常提到他1935年夏躺在格兰切斯特庄园草地上时构想出来的这些神奇的虚拟机器，但是在他后续发表的论文中并没有给出机器的实际格局表。当他在邱奇的指导下写博士论文时，^［21］论文内容已经完全与递归函数和λ函数相关了。