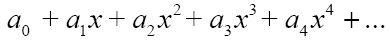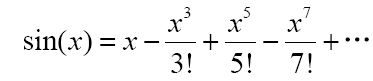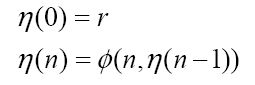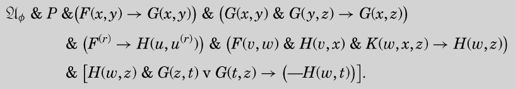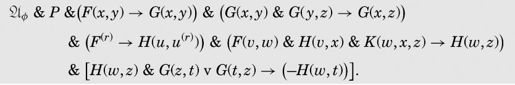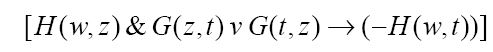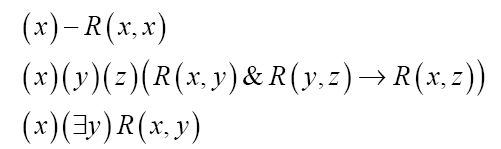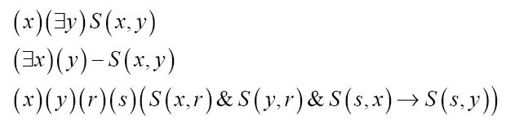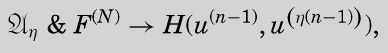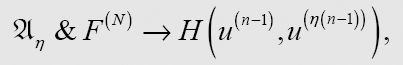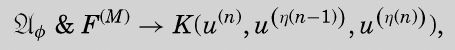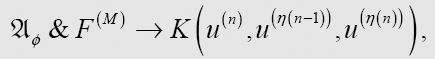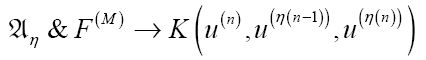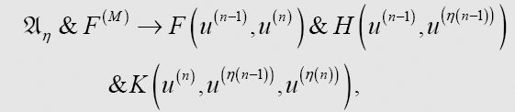We can then show that
    (vii) A power series whose coefficients form a computable sequence of computable numbers is computably convergent at all computable points in the interior of its interval of convergence.
    我们可以证明：
    (vii) 如果一个幂级数的系数构成了一个可计算数的可计算序列，那么这个幂级数在其收敛域内的可计算点处是可计算收敛的。
    一个幂级数是形如：
    We can then show that - 图1
    的无限和。正如我之前介绍的，你可以把三角正弦函数用幂级数形式表示出来：
    We can then show that - 图2
    这些系数（即ai的值）是1、0、-1/3!、0、1/5!、0、1/7!，等等。这些系数当然是一个可计算序列。某些幂级数只有在x等于0时才收敛。另一些则在x的某个值域范围收敛，这个范围称为收敛域。众所周知，正弦函数对于任何x都是收敛的。因为这些系数都是可计算的，所以用机器来判定它们是否收敛是可能的。
    (viii) The limit of a computably convergent sequencee is computable.
    (viii) 可计算收敛序列的极限是可计算的。
    也可能存在一组函数，收敛到某个特定的函数。如果这个收敛是在函数的某个特定值处出现的，称作逐点收敛。更强的函数收敛又称为一致收敛，这种收敛并不依赖于函数的取值。
    And with the obvious definition of “uniformly computably convergent”:
    (ix) The limit of a uniformly computably convergent computable sequence of computable functions is a computable function. Hence
    (x) The sum of a power series whose coefficients form a computable sequence is a computable function in the interior of its interval of convergence.
    根据“一致可计算收敛”的定义，显然有：
    (ix) 由可计算函数组成的一致可计算收敛的可计算序列的极限是一个可计算函数，因此
    (x) 一个其系数形成可计算序列的幂级数的和是在其收敛域内的可计算函数。
    根据这些定理，图灵总结出所有的代数数和一些常见的超越数都是可计算的。
    From (vii) and We can then show that - 图3 we deduce that π iscomputable.
    From We can then show that - 图4 We deduce that e is computable.
    [257]
    From (vi) we deduce that all real algebraic numbers are computable.
    从(viii)和We can then show that - 图5, 我们可推出π是可计算的。
    从We can then show that - 图6可以推出e是可计算的。
    从(vi)中，可以推出所有的实代数数都是可计算的。
    回想一下，代数数是多项式方程的根。
    From (vi) and (x) we deduce that the real zeros of the Bessel functions are computable.
    从(vi)和(x)中，我们推断出贝塞尔函数的实零点是可计算的。
    贝塞尔函数是微分方程的一种常见形式的解。零点就是这些函数取0值的点。最后的结论也包括了三角函数、对数函数、指数函数和一些不太知名的函数。
    图灵之前说要证明定理(ii)，该定理断言任何整数变量的以可计算函数递归定义的函数是可计算的。
    Proof of (ii).
    (ii)的证明。
    在第10节的开始，图灵定义了一个谓词H(x, y)，如果ø(x) = y，则H(x, y)为真。而且介绍了当m ≠ø(n)时，机器如何证明包含We can then show that - 图7和We can then show that - 图8的公式。那个证明建立了函数ø(x)的可计算性。
    当前的证明基于早先的证明，但是这里他用η(x)替换了ø(x)，其中：
    We can then show that - 图9
    Let H(x, y) mean “η(x)=y”, and let K(x, y, z) mean “ø(x, y)=z”.
    令H(x, y)表示η(x) = y，并且令K(x, y, z)表示ø(x, y) = z。
    对于阶乘的例子：
    We can then show that - 图10
    因此K(x, y, z)就是Product(x, y, z)。
    We can then show that - 图11ø is the axiom for ø(x, y).
    We can then show that - 图12ø是ø(x, y)的公理。
    这个We can then show that - 图13φ公理需要提供对谓词K(x, y, z)的支持。对于阶乘的例子，这个公理包括对后继、谓词Sum与Product的公理。下面η(x)的公理更加详尽。
    We that We can then show that - 图14η to be
    We can then show that - 图15
    我们将We can then show that - 图16η定义为：
    We can then show that - 图17
    这是图灵第三次使用名为G的谓词，它们有着不同的定义。然而，这一次的含义最基础：它就是“大于”函数。奇怪的是，图灵并没有澄清这个函数的功能，直到《伦敦数学学会集刊》（Proceedings of the London Mathematical Society）发表了图灵这篇论文的修订稿［3］时才予以说明。（这篇修订稿在本书的第16章）。在修订的论文中，图灵声称G(x, y)可以阐述为“x在y之前”或y > x。像往常一样，F谓词就是后继函数。
    We can then show that - 图18η是7个表达式的合取，以We can then show that - 图19ø和P开始。第三个表达式表明，如果y是x的后继，那么y大于x。第一行的最后一个表达式阐述了G函数的传递性（如果y大于x，z大于y，那么z大于x）。
    第二行的第一个表达式表明 H(u, u(r)为真，这意味着η(0) = r。第二个表达式是：
    We can then show that - 图20
    翻译为非谓语的函数就是，如果w = v + 1，且η(v) = x，ø(w, x) = z ，那么 η(w) = z, 或者:
    We can then show that - 图21
    这是另一种阐述n大于0时η(n)的一般公式的方法。
    We can then show that - 图22η的最后一个表达式是：
    We can then show that - 图23
    注意这里的一对G谓词，它们的参数互换了。这是将G函数并入到此公理的唯一原因。当z不等于t时，G会有一个表达式为真。整个表达式断言，如果H(w, z)为真，那么对所有不等于z的t，H(w, t)为假，换言之，η(w) ≠ t。
    如果We can then show that - 图24η的公式中能够包含许多全称量词，而不是暗示它们的不存在，那么读起来会更加舒服。
    I shall not give the proof of consistenc of We can then show that - 图25η. Such a proof may be constructed by the methods used in Hilbert and Bernays, Grundlagen der Mathematik (Berlin, 1934), p. 209 et seq. The consistency is also clear from the meaning.
    我不会给出We can then show that - 图26η一致性的证明。这些证明可以由希尔伯特和贝奈斯所著《数学基础》（Berlin，1934）一书第209页中所用的方法构造。从这个含义来看，一致性也非常清楚。
    这是指大部分内容由瑞士数学家保罗·贝奈斯撰写的第1卷，他在哥廷根时开始写这本书。因为是犹太人，贝奈斯在1933年失去了教授的职称，并于1934年移居到苏黎世。《数学基础》的第2卷在1939年出版。这本书当时备受推崇，但从未翻译为英文版。贝奈斯在图灵的论文中发挥了另一个重要作用。在图灵发表的论文修订稿中，图灵指出他“感激贝奈斯先生指出这些错误”。阿隆佐·邱奇关于判定性问题无解［4］的短论文也受到相同待遇，他同样附上了修订版［5］，并在脚注上说明“作者感激保罗·贝奈斯先生指出了这个错误”。
    尽管贝奈斯从1935~1936年都在高等研究院，但他在图灵抵达普林斯顿前就回到了苏黎世，很显然他们从没见过面。
    图灵所引用的页数是在数论那一节的开始处。就是在那一页，贝奈斯引入了R谓词，这与图灵的G谓词相同。贝奈斯为他的大于谓词（这里我将其转换为图灵的记号）列举出了公理，可以看出图灵在多大程度上忽略了这些细节：
    We can then show that - 图27
    第三个公理提醒我们，存在一个不大于任何数的数。这个数通常是0或1，依赖于人们对于自然数的定义。在《数学基础》的同一页列出了贝奈斯后继函数（称为S）的公理：
    We can then show that - 图28
    这非常奇怪，因为图灵所引用页定义的谓词正是他在论文中使用的，而他却忽略了这一页上的公理。
    图灵在这里用到了归纳法证明，这种证明方法特别适合数论和其他一些只涉及自然数运算的应用。在归纳法证明中，一个公式（或其他的东西）首先被证明在0时满足。这通常很简单。然后，可以假设当数为n时公式为真。再基于此假设，证明在n + 1时公式也为真。没必要对每一个n证明公式，只要对n为真就能够蕴涵对n + 1也为真。因为公式一开始证明对于0为真，那么对于0 + 1（即1）也为真，而又因为对于1为真，所以对于1+1（即2）也同样成立，依此类推。
    图灵的归纳证明有点不同，他把在0点的证明放在了后面，而以归纳的过程作为开始，并指明如果公式对于n-1为真，那么对于n也为真。他先做了假设。
    Suppose that, for some n, N, we have shown
    We can then show that - 图29
    假设对于某个n和N，我们有：
    We can then show that - 图30
    下面这个公式就是We can then show that - 图31ø公理的直接结果，这个公理支持命题函数K。
    then, for some M,
    We can then show that - 图32
    则对于某个M，
    We can then show that - 图33
    同样，因为We can then show that - 图34很显然，
    We can then show that - 图35
    如果将我们已知为真的表达式在右侧形成合取式，则上式仍为真。一个是用F(M)表示的平凡的后继函数，另一个则是原始的H谓词假设：
    We can then show that - 图36
    We can then show that - 图37
    这里开始采取We can then show that - 图38η公理中的形式，图灵将其抽取了出来：