我的书签
添加书签
移除书签在1983年或是1984年，阿隆佐·邱奇大概80岁时，他被邀请到斯坦福大学的语言和信息研究中心做报告，并参观了中心的Xerox Dandelion计算机。计算机运行的是LISP语言，这是由约翰·麦卡锡（1927—2011）发明的一种编程语言。邱奇被告知，LISP是基于他50多年前发明的λ演算发展而来的。
邱奇坦言他对计算机一无所知，但他的一个学生了解计算机。［1］ 当然，那时所有人都已经知道阿兰·图灵是谁了。
λ演算是阿隆佐·邱奇在20世纪30年代早期为证明一阶谓词逻辑没有通用判定过程而发明的。图灵在发表关于可计算数和判定性问题的论文之前就对此有所了解了。为此，他在论文中增加了一个附录，用来说明他的方法与邱奇的方法在本质上是等价的，这一附录就是本章的主题。
如果说对λ演算的理念觉得很熟悉，那是因为它们对编程语言的发展影响深远。相当早的时候，人们就发现λ演算与划分为过程式或命令式的编程语言之间存在着结构关系，例如早期的编程语言ALGOL［2］，基于这个语言发展出了Pascal和C，同样在C基础上发展出了 C++、Java和C#。用过程式语言编写的程序，其结构围绕着将数据传递给过程（也称为子程序或方法）的理念来组织，过程以各种各样的方式对数据进行处理。
λ演算对LISP、APL、Haskell、Scheme和F#等函数式编程语言有着更直接的影响。在函数式语言中，函数的排列方式更像是链条，后一个函数从前一个函数获得输出。函数式语言通常允许像过程式语言操作数据那样来操作函数。尽管函数式语言没有像过程式语言那样受到主流群体的欢迎，但是最近它们也展露了一些复兴的气息。
阿隆佐·邱奇1903年出生于华盛顿，他职业生涯的大部分时间是在普林斯顿大学度过的。他本科就读于普林斯顿，24岁时获得数学博士学位。在作为国家研究院院士工作两年后，他回到普林斯顿教学，从1929年一直到1967年退休。邱奇后来又在UCLA工作了一段时间，直到1990年。
邱奇是一个勤奋且一丝不苟的人，说话严谨，经常工作到深夜。他的课程经常开始于精心设计的仪式般的擦黑板，有时候还会借助一桶水。在处理数学问题时，他通常会用不同颜色的墨水。当需要更多颜色的时候，他就会按照不同比例混合那些标准颜色的墨水；当完成了一页并要保存起来时，他会用Duco涂满表面。Duco是一种漆，邱奇发现它非常适合保护纸张，因为它不会把纸弄皱。［3］
邱奇指导过31篇博士论文，论文来自于斯蒂芬·克莱尼（1931）、约翰·巴克利·罗瑟（1934）、莱昂·亨金（1947）、马丁·戴维斯（1950）、哈特利·罗杰斯（1952）、雷蒙德·斯穆里安（1959）以及阿兰·图灵（1938）。［4］
通常认为，邱奇建立了符号逻辑协会，因为他是《符号逻辑杂志》的第一位编辑。实际上，他并没有建立这个组织，而是指导杂志取得了辉煌的成功，最突出的是他编纂了重要的逻辑文献书目。
邱奇是在1927年至1929年作为国家研究院院士时开始λ演算的工作的。在那时，数学家们希望理解有效可计算性这个模糊的概念。为了知道数值计算的局限及能力，有必要用形式系统化的方式来定义函数，也就是说用符号、字符串和确定性规则来定义。最好的方法是什么呢？这种方法能否表明这些函数能够充分概括有效可计算性？
邱奇就这一方面的第一篇论文在1931年10月5日被《数学年鉴》收录，并在下一年的4月发表。［5］ 在这篇文章中，邱奇用了一个小写的 lambda（λ）来表示函数。
邱奇引入新记号的一个动机来自于传统函数表示的特定二义性。看看下面的表达式：
x2+5x+7
就表达式本身而言，它在语法上是正确的，但我们仍不知道该对这个表达式做些什么，下面这个就清晰点了：
f(x)=x2+5x+7
这是传统的函数标记法，其中x是约束变量（或自变量）。我们可以按照自己的意愿任意改变约束变量，只要与函数表达式中的其他部分不冲突就行：
f(y)=y2+5y+7
我们可以使用表达式f(4)来表示函数的一个值，用4代替自变量x，并计算函数的值
f(4)=(4)2+5·(4)+7=43
当你意识到这一点时可能会吃惊，那就是没有标准的形式可以将函数表达式（也就是y2+ 5y + 7）与y的具体值一起表示出来。一旦我们用4替换了y，就丢失了自变量信息。如果你需要修复这样的缺点，并发展出一套表示取某个值的函数的方式，可能会想到这样的东西：
y2+5y+7 这其实不算太差，但是如果表达式中含有多个自变量呢？下面的表示就会让人不明就理：
y2+5y+18x-2xy+7 即使你写成：
y2+5y+18x-2xy+7 你假设对x和y按照特定顺序赋值。
在《数学原理》中，怀特海和罗素使用了抑扬符号来表示符合特定函数的类：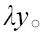
邱奇想把这个抑扬符号移到变量的前面，像^y一样，但因为书写的原因，这个符号后来改成了lambda［6］：λy。
多年来，邱奇的表示法已经有了发展。在下面的讨论中，我使用图灵在其论文附录中使用的表示法。一元变量的函数用下面这个通用形式表示：
λx[M]
其中M是包含自变量x的表达式。对于之前的例子，我们可以表示为：
λx[x2+5x+7]
一个包含特定自变量值的函数可以写成这个通用形式：
{F}(A)
F是函数，如果F含有一个自变量，那么公式代表了函数，其中A代表函数中的自变量。例如，如果函数中的自变量为x，则通用形式为：
{λx[M]}(A)
将M替换为之前的函数，就变成了：
{λx[x2+5x+7]}(A) 若x的值为4，则可以将其写为：
{λx[x2+5x+7]}(4) 现在，我们已经成功地将函数和某个自变量的值表示在一起了。
含有两个自变量的函数有如下一般形式：
{{F}(A)}(B)
为了方便且可读性强，它可以简写为：
{F}(A,B)
如果将F替换为一个真正的函数，它看起来会是：
{λxλy[y2+5y+18x-2xy+7]}(A,B) 我们现在知道A将替代x，B将替代y，它们以前面λ的排列顺序为准。
也可以再简写。如果没有歧义，可以去掉花括号，那么
{F}(A,B)
变成
F(A,B)
这看起来很像常规的函数表示法，但F表达式实际上包含了一些λ：
λxλyM
邱奇还允许将方括号替换为一个点，紧跟在λ串的后面：
λxλy.M(A,B)
这个形式会在接下来的大多数lambda表达式中出现。
邱奇在建立了基本的lambda表示法后，引入了常用逻辑算子的表达式和用于转换为等价公式的替换规则。邱奇以形式化方式定义了这些变换的规则，也可归结为：
I。如果新的自变量不与公式中的其他部分冲突，可以改变某个自变量（例如，x换为y）；
II。在公式{λx.M}(N)中，如果N中不包含x的任何东西，那么可以将N替换到M中任何x出现的位置，这样公式就变成了用N替换原始的x所形成的M；
III。Ⅱ的相反情况仍成立。
在第一篇lambda函数的论文发表一年半后，邱奇发表了第二篇论文［7］。他修正了其给出的假设，并强调：“整个系统的形式字符，使得从符号的本身意义进行抽象，以及将（形式逻辑的）定理证明看做是可以根据一套特定规则在纸上进行推导的游戏成为可能。”［8］这个理念很大程度上符合形式主义的传统。
邱奇也引入了缩写conv来表示“通过转换”，指出利用规则Ⅰ、Ⅱ、Ⅲ可以将一个公式转换为等价形式，例如
λxx2+5x+7convA2+5A+7
邱奇第二篇论文的最后是对正整数的研究。他使用了lambda表示法来定义符号1、后继、加运算、乘运算以及5个皮亚诺公理，并且声明道：“我们的纲领是要在之前所描述内容的基础上建立一套关于正整数的理论，然后，通过已知的方法或是进行适当的改变，将该理论推广到有理数以及实数领域。”［9］
邱奇的学生斯蒂芬·科尔·克莱尼在约翰·巴克利·罗瑟（1907—1989）的帮助下继续下一步的研究。1934年，克莱尼所做的基础工作体现在”形式逻辑的例证”［10］一文中，并简化了多重lambda表示法。之前使用的
λxλyM
现在可以使用
