第6章

加　与　乘

早在1935年5月，阿兰·图灵就考虑去普林斯顿大学，也申请了普林斯顿大学的访问奖学金^［1］。一年后，他发现普林斯顿大学数学系教授邱奇也发表了一篇关于判定性问题的论文，于是图灵“相当肯定地决定”^［2］要去普林斯顿大学。

麦克斯·纽曼为此提供了帮助。纽曼向邱奇介绍了图灵的工作（本书第52页），并在同一封信中，请他帮助图灵获得奖学金：

我应该指出，图灵的工作是完全独立进行的，一直没有得到任何人的指导或者评判。因而，让他尽早接触本领域的顶尖人员变得更加重要，这样他才不致于孤独成性。^［3］

倾向于独立工作，不受外界影响，这实际上是图灵的一个大问题。早在他年轻的时候，图灵就重新创立了二项式理论，并发明了自己的微积分记号。在尝试解决判定性问题时，他不熟悉邱奇及其同事们的早期成果，这也许是件好事，否则他可能就不会找到这样有趣的解决方法了。然而，一般说来，还是有必要知道在世界其他地方发生了什么事情，而对于数理逻辑领域，普林斯顿就是这样的地方。图灵没能获得他申请的普罗科特奖学金，但得到了国王学院的奖学金。

新泽西州普林斯顿的知识光环由于高等研究院的成立而变得更加熠熠生辉。高等研究院的成立得到路易斯·班伯格5百万美元的捐赠。班伯格创建了班伯格百货连锁店，并在1929年经济大萧条之前将其出售给了梅西百货公司。

高级研究院一开始成立的目的是为了促进科学和历史研究。在最初的几年中，高级研究院的数学学院与普林斯顿大学的数学系在同一座楼，这促成了两个机构之间的许多交流。高级研究院迅速成为了优秀科学家和数学家的家园，他们中的一些人是逃离了危险的欧洲来到这里的，其中最有名的是爱因斯坦。他于1933年来到这里，并在此度过了余生。

图灵于1936年9月到达普林斯顿大学时，非常想见到库尔特·哥德尔。一年前，哥德尔还身在高级研究院，之后也回来过，可惜的是一直未能与图灵谋面。

图灵在剑桥大学时见过的约翰·冯·诺依曼此时在高级研究院，还有同样来自剑桥大学的G. H. 哈代。理查德·柯郎和赫尔曼·外尔也在高级研究院，他们几年前逃离了哥廷根。

图灵在普林斯顿大学待了两年，并获得了第二年的普罗科特奖学金（总共2000美元），邱奇成为了图灵的论文指导教授。在邱奇的指导下，图灵写了一篇论文^［4］，并在1938年6月21日获得了博士学位。图灵拒绝了约翰·冯·诺依曼提出的一份1500元年薪、担任其助理的工作，并于一个月后回到了英国。

1939年春，阿兰·图灵回到了剑桥大学，教授数学基础这一课程。四年前，图灵上过麦克斯·纽曼教授的数学基础，并了解了判定性问题。现在，他可以基于自己在可计算数方面的工作，在期末考试中提出关于判定性问题不可解的问题了。^［5］

在论文中，图灵试图让读者相信，他的机器确实可以计算非平凡的数字序列。到目前为止，我们还没有真正见过可以称为计算的东西。在图灵的第一个例子中，表面上看，机器能打印出1/3的二进制表示，但它只是通过笨拙地进行0和1的交替来做到这一点的。当然，这不是用1除以3，机器也没有实现用分子除以分母来计算任意有理数的通用过程。

即使是一个从事处理底层机器代码工作的程序员，也会习惯于可以执行加法和减法等基本数学运算的计算机硬件。出于这个原因，我们可能会怀疑（甚至有点担心）一台甚至连加法都要通过自定义格局和操作来完成的机器。

让我们来构造一个非平凡的机器，当面对峙这种担忧。让我们说服自己，图灵机确实可以作加法和乘法运算（当然还有减法、除法和乘方，甚至是写一首诗）。

第一个例子是一个能够依次算出所有正整数的小图灵机。这个图灵机并不符合图灵的约定，因为它写下的每一个新数字都会覆盖掉之前的数字。在打印结果时，它不跳过任何方格，并用下一个数代替每一个结果。此外，考虑到这些数都是整数，我把机器打印数字的方式设计得跟我们平时写数一样——更高的数位往纸带左边打，而不是右边。尽管没有遵守图灵的约定，但这台机器确实展示了如何通过不断加1让数字递增，这至少是我们对现代计算机的一个基本要求。

在我的例子中，我没有用德文字母，而是用粗体写的描述性单词，（在后面的例子中）有时会用短横线来连接多个单词。和图灵一样，我用“none”来指一个空格。和图灵不一样的是，我用“else”来表明该格局适用于所有其他未明确列出的字符。这个机器从格局begin开始，而且只有三个m-格局。

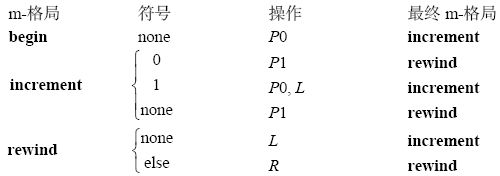
m-格局begin只是打印一个0，然后切换到格局increment。m-格局increment会读取一位数字。如果读到的是0，那么格局increment将它变成1，此时便完成了整个整数的一次递增。如果读到的是1，那么格局increment将其更改为0，然后向左移动一位。现在它必须对更高一位的数字做增量操作。m-格局rewind将读写头向右移至数字的最低位，准备下一次递增。

一旦你开始编写做算术的图灵机，就会立即明白为什么二进制数字这么方便。下面是一个等价的机器，不过它产生的是所有十进制而非二进制的正整数。

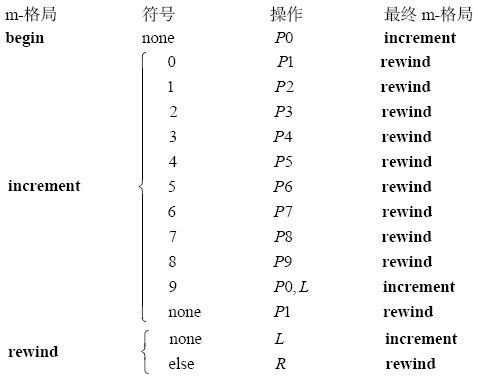
你们看出问题在哪了吧。这台机器需要逐一处理十进制中的每一种数字。二进制系统则更简单，因为它的可能性更少。二进制的加法表和乘法表非常非常小：

我要将这些加法和乘法的运算规则应用在本章的第二个例子中。这是一个遵守了图灵约定的机器，它将会用二进制计算2的平方根。其实，如果假定二进制小数点在所有数位之前，那么机器计算的是

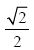
也就是十进制的0.70710678…。为了让讲解清晰易懂，在描述机器时，我将假设它计算的是。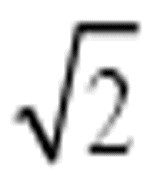

这个机器执行的算法每次计算一个二进制位。假设机器已经运行了一段时间，并已确定了前四位。二进制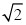的前四位是1.011，相当于十进制的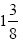或者1.375。下一位是什么？这个机器的策略就是，总是假定下一位是1。要检验这样做是否正确，把1.0111和它自身相乘：

1.0111

x1.0111

——————

10111

10111

10111

00000

10111

——————

10.00010001

这个结果超过了2，所以假设不正确。第五位应该是0，因此得到的前五位变成了1.0110。我们用同样的方法确定第六位。假设第六位是1，让1.01101乘以自身：

1.01101

x1.01101

——————

101101

101101

101101

000000

101101

——————

1.1111101001

得到的结果小于2，所以假设是正确的。我们得到了前六位：1.01101，用十进制表示就是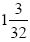或者1.40625。

显然，图灵机需要用乘法来计算2的平方根。一般来说，两个多位数相乘需要其中一个数的每一位和另一个数字的每一位相乘。假设一个数有n位，另一个数有m位，那么数字乘数字的总次数是(n × m)。

手算乘法时，我们一般用一个数的其中一位乘以整个另一个数，产生n个或m个局部乘积，然后再将它们加在一起。我将展示的机器以一种稍有不同的方法进行乘法计算——在乘法过程中始终维护一个过程和。每个位与位相乘的结果都将加进这个过程和中。这种特殊的加法有一个很微妙的地方就是，每个位与位相乘的结果一般来说并不是加到过程和的最低位上，而是中间的某个位置。

例如考虑1.01101乘以它自身。其六位数的每一位都必须与自身以及其他5位相乘，所以肯定需要36次位与位的乘法。乘法本身很简单：当1乘以1时，结果是1；其他情况下，结果是0。这个结果要加到过程和的哪一位取决于相乘的两位在数中的位置。如果将右起第三位乘以右起第四位，其结果会加在过程和的右起第六位。（将开始位记作第0位时，这样会更说得通一些：右起第三位变成了第2位，右起第四位变成了第3位，加起来是5，乘积就该加到这个位置上。）

计算2的平方根的二进制表示时，我们总是需要让一个n位数与自身相乘。如果结果有(2n-1)位，就意味着该结果小于2，那么最后一位是1就是正确的；如果结果是2n位，那么结果将超过2，所以新的最后一位将是0。 这台机器将利用这个结论来确定每一个新的数位是0还是1。

我即将展示的机器符合图灵的约定，这意味着在计算过程中，打印在F-格上的只能是2的平方根中一个接一个的数字。其他的一切——包括维护乘法的过程和——都是在E-格完成的。

这个图灵机还是从m-格局begin开始。它采用@符号而不是中央元音来表示哨兵（在如今的计算机上，这是一个更加简单的符号）。这个图灵机以打印哨兵和数字1开始。

这样，机器开始时所做的唯一假设，就是2的平方根大于1但小于2。

这个图灵机一旦准备好计算新的一位，就会回到m-格局new。这个格局将读写头移动到最左边的数字上。

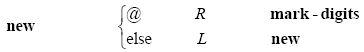
假设机器已经计算出了前几位，让我们来看看机器此后的行为，这样会更容易理解机器的其余部分。下面是一条已经计算出前三位的纸带，这是1.25的二进制表示。机器接着将在标有问号的格子中打印第四位（我将它称为“未知”位）：

这个问号标记是为了方便理解，它并没有真正出现在纸带上，也没有被机器所使用。

准备做乘法时，机器会标记各个数位。（回想一下，图灵定义的“标记”指的是在一个数字的右边打印一个符号。）这些x标记在这台机器中的用法有点类似图灵的范例II（本书第75页）中的机器。m-格局mark-digits将用x标记所有已知的位，z标记未知的位（我将在稍后解释为什么这么做），并在过程和的最低位上打印一个r：

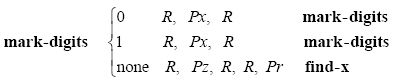
现在，纸带是这样的：

r是过程和的最低位，我们应该把它看作一个0。下面这一段会为每个x打印两个r，并在此过程中擦去x标记。

这个纸带现在有一个七位的过程和，代表初始值0000000：

在过程和中，数位的顺序总是和计算出的数字相反。过程和的最低位在左边。如果未知位是1这个假设是正确的，那么在过程和中初始设定七位就足够了。如果还需要第八位，那么未知的位就是0。

机器中需要自乘的数由已经算好的数（本例中是101）和一个假定为1的新数位组成，所以实际的数是1011。为了记住是哪一位正在乘以其他每一位，机器将用字符x、y和z给数字做标记。在做乘法运算的任何时刻，只有一位标记为x，一位标记为y并且被x标记的数字应当和被y标记的数字相乘。如果标记为x和y的数字正好是同一个，那么我们就使用字符z，所以任何标记为z的数字都将和自身相乘。

这就是为什么未知位（假设为1）有一个初始标记z。第一次的乘法涉及未知位乘以自身。在对后面的格局进行分析时，记住下面这一点将会很有帮助：在乘法运算中，每一位都可能被标记为x，每一位都可能被标记为y，或者仅有一位标记为z。

现在，我们准备开始首次的位与位相乘了。这个机器要么将两个分别标有x和y的位相乘，要么将标有z的位进行自乘。m-格局find-digits先追溯到哨兵，然后转到find-1st-digit寻找最左边那个标记着x、y或z的数字。

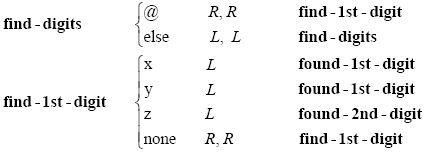
如果find-1st-digit检测到了x、y或者z，它会将读写头置于这一位上。根据不同的标记字母，图灵机将转换到found-1st-digit或者found-2nd-digit。

如果第一个被标记的数字是0，那么我们就不需要第二个数字了，因为无论如何结果都将是0。所以我们可以通过add-zero将0加到当前累积和中。

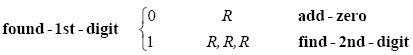
如果第一个数字是1，那么我们必须找到第二位数字。机器会搜索第二个标有x或者y的位。

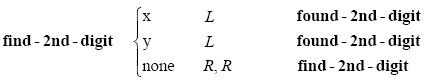
第二位决定了加入过程和的是什么。

需要注意的是，空的F-格是那个未知位，我们已经假定了它是1。在我们的例子中，标记为z的位是未知位，所以add-one会给过程和加1。

给过程和加0通常不会对它有什么影响，但是，不管你向过程和加了什么，机器都需要对其做一些维护。

在我描述怎样初始化右边E-格上的过程和时，我曾指出字母r表示的是0。字母s和t表示的也是0，而u、v、w表示的都是1。当位与位相乘的结果加入过程和时，我们需要多个字母来记录这一结果加到了哪一位上。

m-格局add-zero会将它第一个找到的r变成s，或者第一个u变成v：

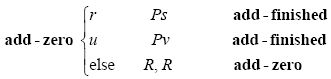
将r（代表0）变成s（代表0）以及将u（代表1）变成v（代表1），可以保证在下次有数字加进过程和时，它会被加到下一位上。

将1加到过程和中需要做的更多。第一个r（代表0）变为v（代表1），或者第一个u（代表1）变为s（代表0）。对于后者，还需要进行进位的操作。

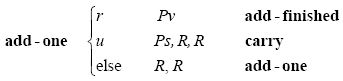
如果进位导致有数字写入了空格中，那么过程和将超过2，这样格局就变为了new-digit-is-zero：

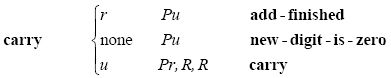
在进行了第一次位与位相乘，并将结果加入过程和中后，纸带变成了：

注意第一个r已经变成了v（代表1）。

现在，必须移动x、y和z标记来表示下一对要相乘的位。一般来说，x标记会左移一个字符。（回想一下，z标记表示x和y标记在此重合，所以这时候标记z会变为y标记，并且x标记印在左边一位）。但是，当标记x到达最后（超过最高位）时，y标记会左移一个字符，x标记移回最右边的数字。当y标记到达最后时，乘法就完成了。

开始时，读写头会移到哨兵点：

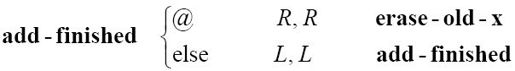
如果erase-old-x找到一个x，那么会把它擦去。如果找到一个z，就会用y取代它。不管是哪种情况，读写头都会移动到左边下一个E-格：

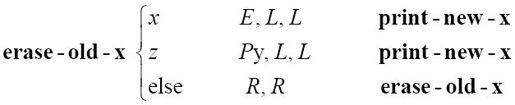
现在可以打印下一个x标记了：

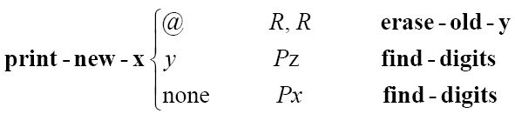
我们例子中的纸带现在可以回到find-digits步骤，为下一次的位与位相乘做准备了：

这次位与位相乘后会将另一个1加入过程和，只不过这一次将加在后面一位上，因为它总是会加到最左边的r或者u上：

机器接着将标记x向左移动一个位置：

这次位与位相乘的结果是0，过程和的值并不改变，但是最左边的r会变为s：

标记x再次左移：

新的位与位相乘的结果使得最左边的r变成v：

现在，x马上就要移进哨兵的位置了。这种情况就由erase-old-y和print-new-y处理：

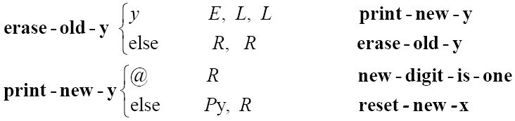
值得注意的是，如果标记y也要移进哨兵的位置了，整个乘法就结束了，并且过程和没有溢出分配给它的空间。这样我们就知道了，未知位是1。

否则，标记x必须重置到数的最低位，也就是未知位：

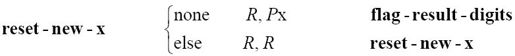
例子中，纸带的标记x和y现在如下所示：

我们还需要做许多事情。下一个位与位相乘的结果需要加到过程和的第二位上。为此，当前累各和的第一个s或者v要（对应地）变为t或者w：

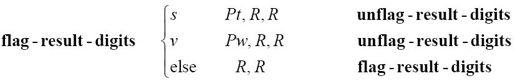
剩下的s和v则（对应地）变为r和u：

这个过程确保下一个位与位相乘的结果会加到过程和的正确位置。

现在纸带真正做好了进行下次位与位相乘的准备，这个位与位相乘的结果会加到过程和中第一个r或者u的地方。

整个乘法将会以两种方式中的一种结束，这两种方式你都已经看到过了。如果机器试图将过程和进位到一个空格中，那么我们知道结果肯定会超过2，未知位一定是0，格局就会变成new-digit-is-zero。或者，如果y标记下一步该到哨兵的位置，那么整个乘法就完成了，并且过程和没超过2，格局变为new-digit-is-one。

这两块基本上是一样的。首先，机器会回到哨兵点：

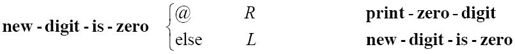
现在，机器可以找到空格，并在那里打印0。在移过所有数字的时候，它可以擦除所有还留着的标记。

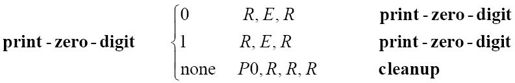
类似地，m-格局new-digit-is-one会打印一个1，作为新的数位，然后也进入cleanup模式：

在打印出新的数位后，m-格局cleanup移除过程和，然后为计算下一个数位跳转到new格局。

这样，例子中纸带的第四位就计算出来了，现在可以准备计算第五位了。

很明显，图灵机并不是一个对程序员友好的环境。大部分编程语言都会有一个叫做sqrt（或类似）的函数，它可以计算2甚至任何其他数的平方根。

然而，这些平方根函数往往都有精度限制。现在的大部分计算机语言都采用美国电气和电子工程师协会（IEEE）的标准来存储浮点数。一个双精度的浮点数只能存储精确到52位的二进制小数，或者大约15到16位左右的十进制小数。如果你需要一个更加精准的数字，很可能就要自己想办法了（直到最近，才出现了很多更高精度的数学函数）。要想像图灵机那样能执行任意多位数的运算，你会发现你要做的会和我刚刚描述的过程差不了多少。

在一台真实的计算机上，你至少可以很方便地进行加法和乘法运算。如果你眼前的任务在一台图灵机上实现几种不同类型的函数，你可能需要考虑组建一个常用表集，作为积木来搭建一些更为复杂的表。

这正是图灵下一步所做的，虽然他的真正目标是建立一个可以模拟任何其他机器的通用机。