第9章

    通　用　机

    图灵在论文下一节所描述的机器就是我们今天熟知的通用图灵机，之所以称为通用机，是因为我们只要有了这种机器就足够了。之前介绍的特殊计算机器既不能保证按类似的方式执行，甚至也没有通用的零件。而通用机在获得其他机器的标准描述后就可以模拟它们。如今我们可以说，通用机是可编程的。

    6. The universal computing machine.
    It is possible to invent a single machine which can be used to compute any computable sequence. If this machine 第9章通 用 机 - 图1 is supplied with a tape on the beginning of which is written the S.D of some computing machine 第9章通 用 机 - 图2,
    [242]
    then 第9章通 用 机 - 图3 will compute the same sequence as 第9章通 用 机 - 图4. In this section I explain in outline the behaviour of the machine. The next section is devoted to giving the complete table for 第9章通 用 机 - 图5.
    6. 通用计算机器
    发明一台可以计算任何可计算序列的机器是可能的。如果为机器第9章通 用 机 - 图6提供一条纸带，纸带开头写入的是某台计算机器第9章通 用 机 - 图7的标准描述，那么第9章通 用 机 - 图8可以计算出与第9章通 用 机 - 图9相同的序列。在这一节中，我将概括地介绍这种机器的行为。下一节着重给出第9章通 用 机 - 图10的完整表。

    这里再次使用了手写字体。图灵使用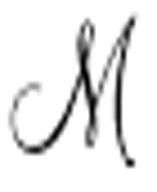第9章通 用 机 - 图11表示任意一台机器，而使用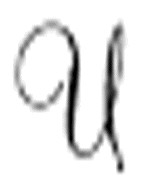第9章通 用 机 - 图12表示通用机。

    当我们说到计算机程序的时候，通常会涉及输入和输出。一段程序读取输入，写出输出。但是到目前为止，我们描述的机器基本上都没有输入，因为它们是以空白纸带开始的。这些机器产生0和1序列形式的输出，输出序列中可能会临时散布一些其他用作标记或便笺的字符。

    相反，通用机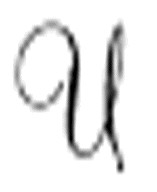第9章通 用 机 - 图13要求实际输入，特别地，要求纸带上包含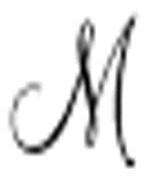第9章通 用 机 - 图14的标准描述&md;&md;字母A、C、D、L、N、R构成的描述了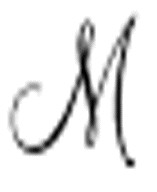第9章通 用 机 - 图15所有格局的序列。机器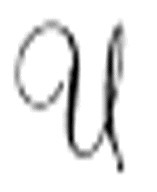第9章通 用 机 - 图16读入并解释这个标准描述，然后打印出和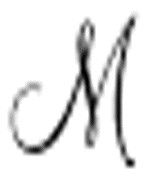第9章通 用 机 - 图17一样的输出。

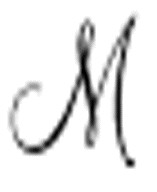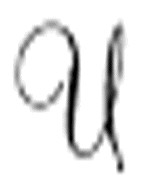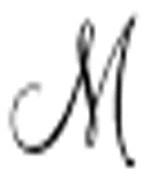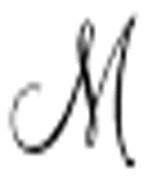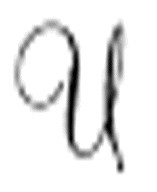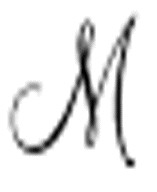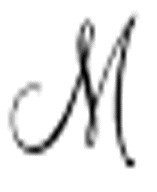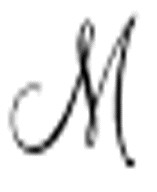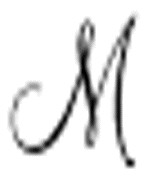    但是这并不完全正确：第9章通 用 机 - 图18的输出和第9章通 用 机 - 图19的输出可能不完全相同。通常情况下，第9章通 用 机 - 图20不能完全模仿第9章通 用 机 - 图21。机器第9章通 用 机 - 图22可能以一个空白的纸带开始，但第9章通 用 机 - 图23不是这样，提供给它的纸带已经包含了第9章通 用 机 - 图24的标准描述。如果第9章通 用 机 - 图25违反了图灵的约束，向两个方向输出，会出现什么情况呢？准确地模仿第9章通 用 机 - 图26将导致重写第9章通 用 机 - 图27的标准描述。

    图灵说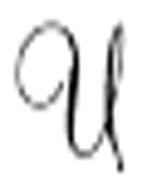，第9章通 用 机 - 图28会配有一条以机器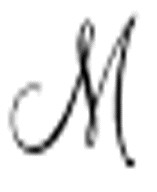第9章通 用 机 - 图29的标准描述开头的纸带。如果纸带的两个方向都是无限延伸的，就没有“开头”一说了。图灵暗含的意思是，将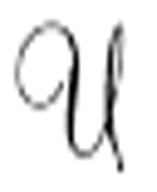第9章通 用 机 - 图30的输出写到纸带上的标准描述之后。

    如果考虑机器只向一个方向打印（正是图灵的约束），那么我们能写出一个通用机，让它读取纸带开头处某台机器的标准描述，然后在标准描述后面无限的空白区域里精确地复制出该机器的输出吗？

    这似乎不太可能。无疑，通用机需要自己的便笺空间，因此它的输出和它尝试模仿的机器的输出是不同的。即使我们仅仅要求通用机复制机器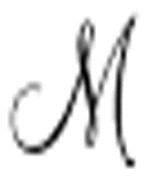第9章通 用 机 - 图31的F-格，这台通用机也明显会比图灵之前描述的机器复杂得多。

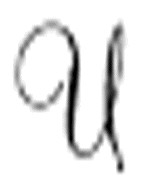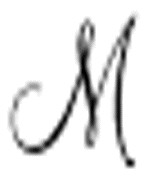    图灵不能保证他的通用机能够如实地复制它正在模仿的机器的输出。他只说：“第9章通 用 机 - 图32会计算出与第9章通 用 机 - 图33相同的序列。”事实上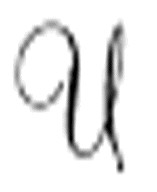，第9章通 用 机 - 图34会在序列之外打印很多额外的输出。

    图灵从一个很奇怪的角度着手通用机的设计。

    Let us first suppose that we have a machine 第9章通 用 机 - 图35′ which will write down on the F-squares the successive complete configurations of 第9章通 用 机 - 图36.
    首先假设我们有一台机器第9章通 用 机 - 图37′，它会在纸带的F-格处写下第9章通 用 机 - 图38的连续完全格局。

    如前所述，完全格局是完成一个操作后纸带的快照，连同读写头的位置和下一个m-格局。这些连续的完全格局提供了机器完整的历史操作记录。

    These might be expressed in the same form as on p. 235, using the second description, (C), with all symbols on one line.
    这些可以使用同第235页一样的形式表达，使用第二种描述(C)，并且所有的符号都在同一行。

    本书第82页用了如下的序列展示信息：

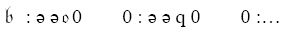
    第9章通 用 机 - 图39

    在该记法中，连续的完全格局间使用冒号隔开。在每一个完全格局中，表示下一个m-格局的德文字母放在下一个扫描符前面。

    Or, better, we could transform this description (as in §5) by replacing each m-configuration by “D” followed by “A” repeated the appropriate number of times, and by replacing each symbol by “D” followed by “C” repeated the appropriate number of times. The numbers of letters “A” and “C” are to agree with the numbers chosen in §5, so that, in particular, “0” is replaced by “DC”, “1” by “DCC”, and the blanks by “D”.
    或者，更好的方法是，用D后跟适当数目的A所构成的字符串代替每个m-格局，用D后跟适当数目的C所构成的字符串代替每个符号，以此来转换当前的描述（如§5）。字母A和C的数目和§5中的数目是一致的，因此，0使用DC代替，1用DCC代替，空则由D代替。

    图灵提出这种标准描述（他这么称）来编码机器的状态。现在，他提出再使用它来表示完全格局。

    These substitutions are to be made after th complete configurations have been put together, as in (C). Difficulties arise if we do the substitution first.
    只有在完全格局组合在一起后，才能进行这些替换，比如在(C)中。如果先进行替换会出现问题。

    我猜想，图灵这里想要表达的意思是，由于m-格局和符号要被多个符号代替（比如，1变成DCC），因此在查找下一个格局的时候必须注意滑动一些格，以防破坏某个符号的编码。

    In each complete configuration the blans would all have to be replaced by “D”, so that the complete configuration would not be expressed as a finite sequence of symbols.
    每个完全格局中的空白都必须用D替换，因此，完全格局不能表示成一个有限的符号序列。

    字母D代表一个空格。图灵不想在一个完全格局中出现任何中断。他想使每个完全格局都是一个没有中断、连续的字符串。他的原话是这样的：“因此，完全格局不能表示成一个有限的字母序列。”这样的表达不是很明确。我觉得“不能”应该是“现在”。很明显，他不想用一个由符号D构成的无限序列来表示一个空白的纸带，每一个完全格局都是有限的。

    If in the description of the machine II of §3 we replace “第9章通 用 机 - 图40” by “DAA”, “第9章通 用 机 - 图41” by “DCCC”, “第9章通 用 机 - 图42” by “DAAA”, then the sequence (C) becomes:
    DA: DCCCDCCCDAADCDDC: DCCCDCCCDAAADCDDC:…(C1)
    (This is the sequence of symbols of F-squares.)
    如果在§3机器II的描述中，把第9章通 用 机 - 图43替换成DAA，把第9章通 用 机 - 图44替换成DCCC，把第9章通 用 机 - 图45替换成DAAA，则序列(C)变成：
    DA：DCCCDCCCDAADCDDC：DCCCDCCCDAAADCDDC：…( C1)
    （这是F-格处的符号序列。）

    图灵并没有提到他所做的所有替换。他还把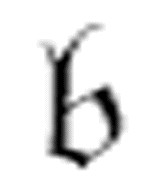第9章通 用 机 - 图46替换成了DA，空白替换成了D，0替换成了DC。

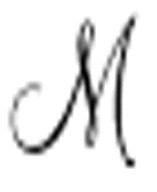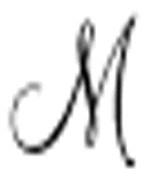    括号里的说明指的是图灵提出的机器第9章通 用 机 - 图47′的输出方式。正常的机器第9章通 用 机 - 图48在F-格处打印0和1，并且用E-格处的其他符号来辅助计算0和1。机器第9章通 用 机 - 图49′在F-格处打印机器第9章通 用 机 - 图50的连续的完全格局，并且使用E-格辅助构造这些连续的完全格局。

    用这种方式表示的完全格局是很难阅读的。正如前面所说的，需要注意的是D，它可以表示一个格局或者一个符号。

    ⟩ 如果D后接的是一个或多个A,那么它是一个格局。格局编号是A的数目。
    ⟩ 如果D后接的不是A，则它是一个符号。在这种情况下，D后接的可能是0个或多个C。如果D单独出现，则它代表一个空白；否则，DC 代表0，DCC 代表1，后接多个C则指示其他符号。
    It is not difficult to see that if 第9章通 用 机 - 图51 can be constructed, then so can 第9章通 用 机 - 图52′. The manner of operation of 第9章通 用 机 - 图53′ could be made to depend on having the rules of operation (i.e., the S.D) of 第9章通 用 机 - 图54 written somewhere within itself (i.e. within 第9章通 用 机 - 图55′); each step could be carried out by referring to these rules.
    不难看出，如果我们能构造出第9章通 用 机 - 图56，那么我们也能构造出第9章通 用 机 - 图57′。第9章通 用 机 - 图58的操作规则（即标准描述）可以写进自身（即第9章通 用 机 - 图59′）的某个地方由它来决定第9章通 用 机 - 图60′的操作方式，每一步都可以由这些规则算出来。它的每一步操作都可以参考这些规则来执行。

    把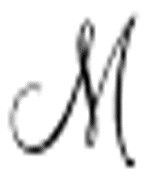第9章通 用 机 - 图61的标准描述写进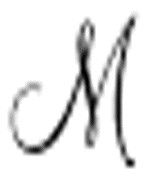第9章通 用 机 - 图62′的某个地方，这是一个全新的概念。它是如何写的呢？如何访问它呢？图灵追求机器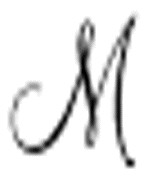第9章通 用 机 - 图63′的方式有点偏离他的目标，虽然看上去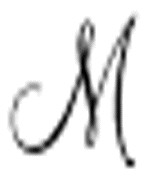第9章通 用 机 - 图64′确定是可以构造出来的。

    We have only to regard the rules as being capable of being taken out and exchanged for others and we have something very akin to the universal machine.
    我们只需要认为这些规则是可以取出并替换的，那么我们便得到了某种本质上非常类似通用机的东西。

    现在问题变得清晰点儿了。图灵在本节开头说过，要为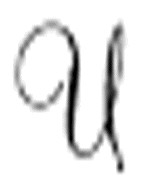第9章通 用 机 - 图65提供一个包含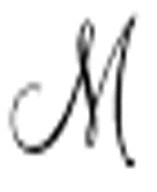第9章通 用 机 - 图66的标准描述的纸带。这正是“这些规则可以取出并替换的”要表达的意思。我们可以为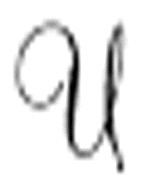第9章通 用 机 - 图67提供一个包含任何想要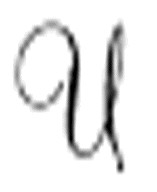第9章通 用 机 - 图68模仿的机器的标准描述的纸带。

    抽象地来看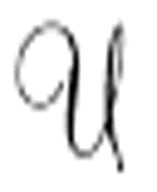，第9章通 用 机 - 图69现在变得几乎是，嗯，也不完全是显然的，但仍然已经简单了很多。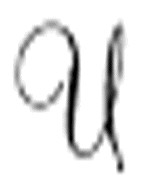第9章通 用 机 - 图70以一个打印着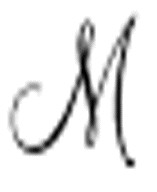第9章通 用 机 - 图71的标准描述的纸带开始。这个标准描述负责打印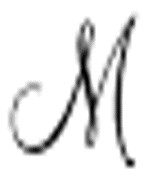第9章通 用 机 - 图72的连续完全格局。标准描述和完全格局使用相同的编码方式：每个完全格局包含一个字母序列，这些序列大多指示纸带上打印的符号。每个完全格局还包含了一个以D开头、后接若干个A的字符串，用来表示位于扫描符前面的下一个格局。例如：