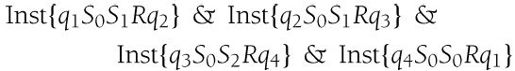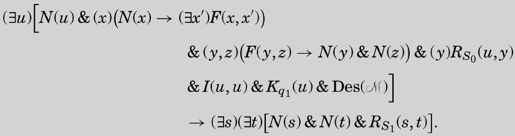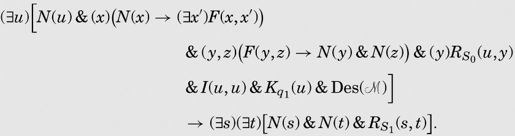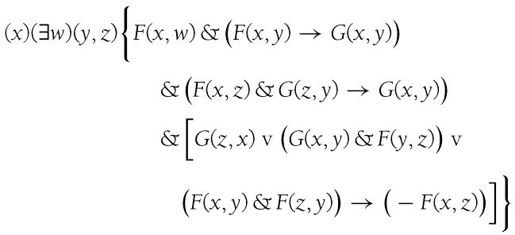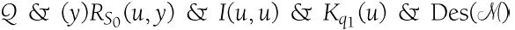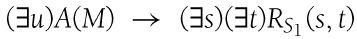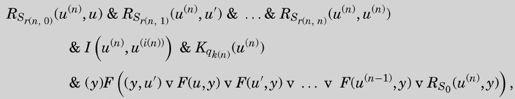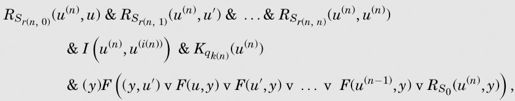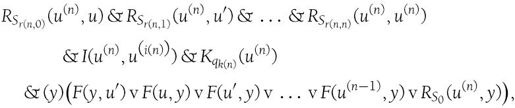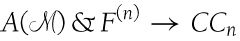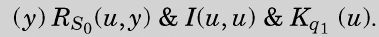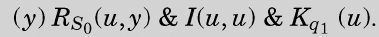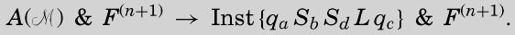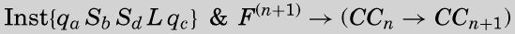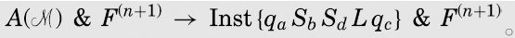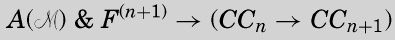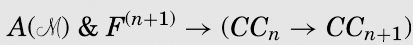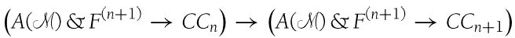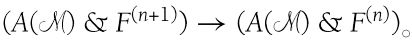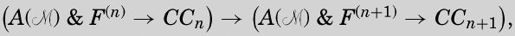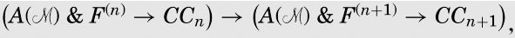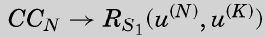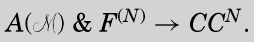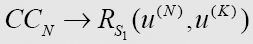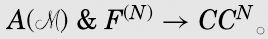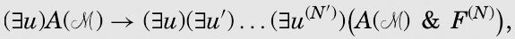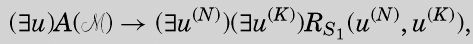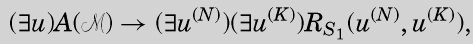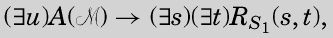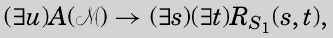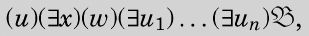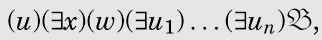第14章

主要证明

有些数学证明直截了当，有些则需要一些拐弯抹角的方法。后一种当然包含了归谬法，先假设所要证明结论的反论题成立，然后证明依据初始假设推导会导致矛盾。

还有一些方法既不从正面证明，也不从反面证明，它构建出显得有些神秘而放任的详尽结构，看起来似乎完全回避了证明的对象。正当推导的整个中心变得完全模糊，你准备放弃看到结果的希望时，突然灵光浮现，聪明的数学家就完成了证明。

在某种意义上，图灵论文的最后一节最重要，因为图灵正是在这里阐述了“判定性问题不可解”。这在当时是一个非常重要的结论，图灵构建的结构支撑了这一结论（现在称为图灵机的虚构设备），最终比现在吸引我们注意力的实际证明更显得有趣，也更硕果累累。

图灵在论文的第8节为这个证明做了铺垫。虽然这在当时还显得并不重要，但他还是很仔细地证明了，不能设计一台执行通用有限过程的图灵机来判定另一台图灵机是否打印了数字0。中间两节（9和10）表明了，图灵关于机器可计算性的概念与我们习惯的人的可计算性的概念是等价的。

在第11节，图灵介绍了计算机器的功能是如何使用一阶谓词逻辑语言表示的。然后他以这种逻辑构造了一个公式，当且仅当机器打印了数字0时公式才是可证明的。如果公式是可判定的，也就是说，如果可以判定它是否是可证明的，那么我们可以构造一个通用过程来判定机器是否打印了0，我们已经知道这是不可能的。

[259]

11. Application to the Entscheidungsproblem.

The results of §8 have some important applications. In particular, they can be used to show that the Hilbert Entscheidungsproblem can have no solution. For the present I shall confine myself to proving this particular theorem. For the formulation of this problm I must refer the reader to Hilbert and Ackermann's Grundzüge der Theoretischen Logik (Berlin, 1931), chapter 3.

11. 在判定性问题中的应用

§8中得到的结论有一些重要的应用，特别是可以用来证明希尔伯特的判定性问题无解。现在，我就来证明这个定理。至于这个问题的构造，我强烈建议读者阅读希尔伯特和阿克曼所著的《数理逻辑原理》（Grundzüge der Theoretischen Logik，Berlin，1931）的第3章。

那本书实际上是1928年出版的，共四章120页，第3章大概位于该书的三分之一处，章名是Der engere Funktionenkalkül，即“受限函数演算”，也就是我们今天熟知的一阶谓词逻辑。作者写道：

Das Entscheidungsproblem ist gelöst, wenn man ein Verfahren kennt, das bei einem vorgelegten logischen Ausdruck durch endlich viele Operationen die Entscheidung über die Allgemeingültigkeit bzw. Erfüllbarkeit erlaubt…. [Das] Entscheidungsproblem mu als das Hauptproblem der mathematischen Logik bezeichnet werden.^［1］

当我们知道一个有限操作的过程可以确定任何给定表达式的正确性和可满足性时，这个判定性问题就是可解的……判定性问题理应看作数理逻辑的主要问题。

这里，希尔伯特和阿克曼使用正确性（validity）和可满足性（satisfiability）来表明判定性问题的语义形式。25年后，威廉·阿克曼在他的小书《判定性问题的可解情况》（North-Holland出版公司，1954）中从语义角度继续研究了判定性问题。

图灵使用了一些稍微不同的词语来描述判定性问题。他用K（可能代表Kalkül）来表示希尔伯特的受限函数演算。

I propose, therefore, to show that there can be no general process for determining whether a given formula of the functional calculus K is provable, i.e. that there can be no machine which, supplied with any one of these formulae, will eventually say whether is provable.

因此我认为，不存在一个通用过程来判定一个给定的函数演算K的公式是可证的，也就是说，不存在这样的机器：为它提供这些公式中的任意一个，而最终能说明 是否可证明。

通过使用词“可证明”，而不是“正确性”或“可满足性”，图灵表明他正在从句法的角度接近判定性问题。逻辑的句法方法与公理和推理规则系统相关。一个公式被认为是可证明的（也就是说，该公式是定理），只有当它是公理或者可以使用推理规则从公理中推导出来时才成立。一阶逻辑的语义和句法方法等价于哥德尔在1930年提出的完备性定理。

根据第9节和第10节的讨论，图灵现在可以声明，如果没有机器可以实现通用判定过程，那么也不存在人可以进行的通用判定过程。

在1936年，阅读图灵论文的读者并不精通完备性、不完备性和可判定性之间的细微区别，可能会困惑于哥德尔的不完备性证明（出现在一篇标题中含有unentscheidbare Sätze即“不可判定命题”的论文中）和图灵的证明之间的关系。事实上，图灵在论文的第一页已经说了“可以得到与哥德尔的结论大致相似的结论”（本书第57页）。他需要在这个主题上更详尽地阐述一下。

It should perhaps be remarked that what I shall prove is quite different from the well-known results of Gö^†. Gödel has shown that (in the formalism of Principia Mathematica) there are propositions such that neither nor — is provable. As a consequence of this, it is shown that no proof of consistency of Principia Mathematica (or of K) can be given within that formalism. On the other hand, I shall show that there is no general method which tells whether a given formula is provable in K, or, what comes to the same, whether the system consisting of K with — adjoined as an extra axiom is consistent.

^† Loc. cit.

这里需要注意的是，我将要证明的结论与著名的哥德尔的结论^†非常不同。哥德尔已经表明（在数学原理的形式主义中）存在命题，使得和-不可证明。这个结论的结果表明，在该形式范围内不能给出数学原理（或者K）的一致性的证明。另一方面，我将展示的是不存在一个通用方法来判定一个给定的公式在K中是否可证明，或者换一种表达方式，由K和一条额外公理公-组成的系统是否一致。

^† Loc. cit.

哥德尔的定理和图灵的定理从相反的方向来处理可判定性。哥德尔的定理表明，存在既不能被证明又不能被反驳的命题。这些命题称为不可判定的。

图灵提及的“一般方法”是一个判定过程：对任何公式进行分析并判定其可证明还是不可证明的算法。图灵将证明不存在这样的通用判定过程。

即使存在不可判定命题，我们也能想象存在一个判定过程。在分析哥德尔的不可判定命题时，需要意识到命题及其反命题都是不可证明的。

If the negation of what Gödel has shown had been proved, i.e. if, for each , either or — is provable, the we should have an immediate solution of the Entscheidungsproblem. For we can invent a machine which will prove consecutively all provable formulae. Sooner or later will reach either or — . If it reaches , then we know that is provable. If it reaches — , then, since K is consistent (Hilbert and Ackermann, p. 65), we know that is not provable.

如果哥德尔所宣称命题的反命题已经被证明，即如果对于每一个，或-都可证明，那么我们应该能够立即得到判定性问题的解。因为我们可以发明一台机器，它可以相继证明所有可证明的公式，这台机器早晚会证明或-。如果证明了，那么我们就知道可证明。如果证明了-，那么因为K是一致的（《希尔伯特和阿克曼》，第65页），所以我们知道是不可证明的。

但是图灵令人捉摸不透的机器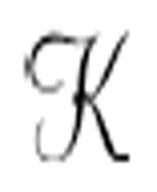（这是论文最后一次提到）显然不是希尔伯特在将判定性问题形式化时所想的。不管任何假想的判定过程是如何的“机械”或者“像机器”，它仍然被看成是人可管理的，而不是一台需要上千年的处理时间和世界上所有内存资源的计算机。

哥德尔的结论并没有奠定一个通用判定过程的基础，图灵的证明仍然是必须的。

Owing to the alsence of integers in K the proofs appear somewhat lengthy. The underlying ideas are quite straightforward.

Corresponding to each computing machine we construct a formula Un () and we show that, if there is a general method for determining whether Un () is provable, then there is a general method for determining whether ever prints 0.

由于K中不存在整数，因而证明会显得有点冗长，但根本的思想还是相当直接的。

对应于每个计算机器，我们都构造一个公式Un()，并且表明，如果存在一个通用的方法可以判定Un()是否可证明，则存在一个通用的方法来判定是否打印了0。

图灵是不是在这里过早地抖了包袱，用“不可判定”（Undecidable）来命名公式Un呢？这个Un(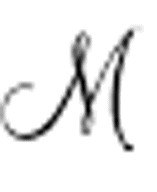)公式起到了反例的作用——没有可以成功进行分析的通用判定过程。

你可能会想起，机器包含了一系列与操作相关的格局。在图灵介绍通用机的最初几页，他使用“指令”一词来表示这些组成机器的基本元素。

图灵需要用一阶逻辑语言来表示这台计算机器。每一个指令将会转换为一个公式，这个公式表明了指令是如何影响机器的完全格局的。你可能还记得，完全格局是在机器进行每一次移动后纸带的快照。完全格局也包括机器的下一个m-格局和下一个扫描符。

图灵首先给出几个命题函数（用现代的术语说就是谓词）。和所有的命题函数一样，它们存在真值，或真或假。在所有情况下，这些函数的参数都是非负整数，用来标注纸带上的方格及完全格局。我们假定，纸带上的方格是以0开始编号的，这表明纸带是有起始的，并且只在一个方向上无限延伸。

完全格局也假设为是依次标号的。数字对(x, y)表示完全格局x中的特定格y。尽管我会在例子中使用实际的数，但在图灵的讨论中没有出现任何数字或例子。

我们回想一下图灵的样机I，它每隔一格交替打印0和1。下面是前10个完全格局。我已经在最左列用数字标识了这些完全格局（标题CCx意思是“完全格局x”），并在顶部用数字标识了纸带上的方格。同时，我用带下标的q代替了图灵原来用于表示格局的字母。

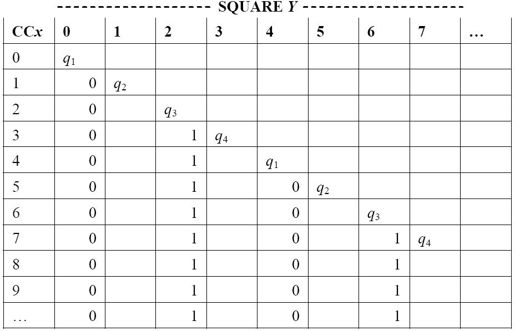
这台机器只是每隔一格打印，因此只有偶数编号的方格才包含数字。出现在方格中的m-格局表明，这个方格会在这个完全格局中被扫描。

图灵的许多命题函数都包含了作为函数名一部分的下标。这些命题函数是被独立定义的，很快你会看到图灵是如何使用它们来描述整台机器的。

The interpretations of the propositional functions involved are as follows:

R_Sl(x,y) is to be interpreted as “in the complete configuration x (of ) the symbol on the square y is S”.

所涉及的命题函数的解释如下：

R_Sl(x, y)可以解释为“在（的）完全格局x中，y格中的符号是S”。

结尾引号前的S漏了下标l。回想一下，S₀是一个空格，S₁是0，S₂是1。在样机I中，R_S2(5, 2)为真，因为数字1出现在完全格局5的第2格中； R_S2(5, 6)为假，因为数字1没有出现在完全格局5的第6格中。

[206]

I(x, y) is to be interpreted as “in the complete configuration x the square y is scanned”.

I(x, y)可以解释为“在完全格局x中，y格会被扫描“。

在样机I中，函数I(6, 6)为真，因为在完全格局6中下一个扫描格是6，但I(6, y)对于其他任何y格都为假。

K_qm(x) is to be interpreted as “in the complete configuration x the m-configuration is q_m.

K_qm(x)可以解释为“在完全格局x中的m-格局为q_m。

句子末尾少了半个引号。对于样机I，函数K_q2 (5)为真，而K_q3和K_q2(7)为假。

F(x, y) is to be interpreted as “y is the immediate successor of x”.

F(x, y)可以解释为“y是紧邻x的后继”。

用特殊算术记号表示就是y = x + 1。使用图灵早先引入的自然数记号，谓词F(u″′, u″″)为真，但是经过适当的公理化后，F(u″′, u″″)应该为假。

到目前为止，图灵仅仅讲述了用来描述运行中机器的完全格局的命题函数。他还未将它们与描述真实机器的格局表中的项对应起来。一台机器的标准形式是每行只包括一条打印指令和一条移动指令。格局表的每一行包含一个m-格局q_i、 一个扫描符S_j、一个打印符S_k（可以与S_j相同），读写头的移动方向（向左、向右或根本不移动），以及新的m-格局q_l。

图灵接下来给出了他称为Inst（代表“指令”）的概念。这并不是一个命题函数，而是从刚才给出的命题函数得出的表达式的缩写。每一个指令表达式都会与格局表中的一行关联。这个表达式描述了这些m-格局、符号和读写头移动的特定组合对完全格局的影响。

Inst {q_i S_j S_k L q_l} is to be an abbreviation for

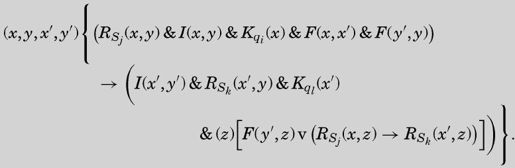
指令{q_i S_j S_k L q_l}是以下表达式的缩写：

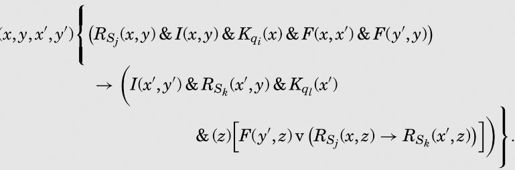
这是三个可能的指令表达式中的一个，适用于读写头向左移动的情况，指令参数中的L表达了这个含义。

首字母(x，y，x′，y′)是四个全称量词(x) (y) (x′) (y′)的缩写。约束变量x和x′是两个连续的完全格局。在第一行的最后你会看到谓词F（两个谓词中的第一个），表示x′是x的后继。约束变量y和y′是两个邻接的方格。对于向左移动读写头的指令，y′等于y减去1，即y是y′的后继，正如第一行的第二个谓词F所表明的。

第一行中的其他三个谓词给出了当前指令的条件。完全格局为x，扫描格为y，扫描符为S_j，格局为q_i。

第二行以一个蕴涵符开始，作用于表达式余下的所有部分。这些是描述由这条指令得到的完全格局的谓词。在下一个完全格局x′中，将扫描y′格，y格中的当前符号为S_k，新的m-格局为q_l。

指令在第三行以一个表达式结束，该表达式表明除了y格外的所有其他格都必须保持不变。这些格用约束变量z表示。z要么是y′的后继（此时z等于y并将被打印）或者……但是图灵余下的公式是错的。他说在其他所有的格中，S_j替换为S_k，而这没有意义。

对指令表达式更好的阐述是在原论文发表大约一年后，图灵发表在《伦敦数学学会集刊》上的论文修订版。修订版（本书第295页）也不是完全正确的，最后一行应该是：

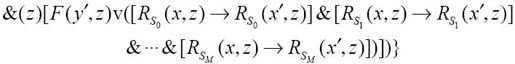
R函数的下标S₀, S₁,…, S_M都是可以打印的符号。也就是说，对于所有的z格，要么z是y′后继（也是说，z就是y——调整过的方格），要么在从完全格局x转到完全格局x′ 时方格中的符号保持不变。

图灵刚刚展示的指令表达式针对读写头向左移动的情况。

Inst {q_i S_j S_k R q_l} and Inst {q_i S_j S_k N q_l}

are to be abbreviations for other similarly constructed expressions.

指令{q_i S_j S_k R q_l}和{q_i S_j S_k N q_l}是其他相似构造表达式的简写。

为了多展示点（也为了更方便地参考），下面的框中展示了读写头向右移动时指令的正确表达式。

指令{q_i S_j S_k Rq_l}是以下表达式的缩写：

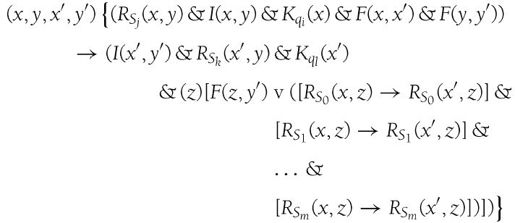
这个表达式几乎和读写头向左移动的一样，除了F(y′, y)变为了F(y, y′)，表明新的扫描格是在上次扫描格的右侧；同样，表达式后面部分的F(y′, z)变为了F(z, y′)，用来表示z等于y。

对于样机I，R_Sm函数的下标m的最大值为2，因为机器只打印符号S₀（空）、S₁（0）和S₂（1）。

Let us put the description of into the first standard form of §6. This description consists of a number of expressions such as “q_i S_j S_k L q_l” (or with R or N substituted for L).

让我们把的描述变成§6中的第一个标准形式。这个描述包含了很多表达式，例如{q_i S_j S_k L q_l}（或者用R或N代替L）。

实际上，图灵是在第5节设计这个标准形式的。在其论文第241页（本书第126页）的样机I是这样的：

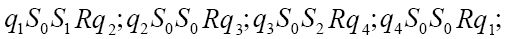
四个五元组中的每一个为一个指令表达式。

Let us form all the corresponding expressions such as Inst {q_iS_jS_kLq_l} and take their logical sum. This we call Des ().

我们来构造出所有对应的表达式，例如指令{q_i S_j S_k L q_l}，并计算它们的逻辑和。我们称之为Des()。

这是机器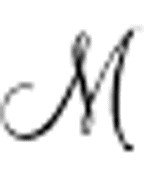的描述。术语“逻辑和”有些模糊，因此在修订版（本书第297页）中图灵使用“合取”代替了这个词。换句话说，所有指令术语都可以用&连接，以一阶逻辑语言表示整个机器。

样机I的Des()是下列表达式的缩写：

现在，图灵将把Des(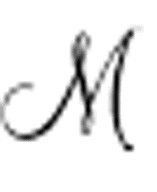)公式代入更大的公式Un(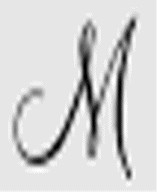)中，即不可判定公式。这个公式是形如下式的蕴涵关系：

某个机器 → 打印0

公式同时使用了后继函数F及命题函数N，其中如果参数为自然数，N为真。

The formula Un() is to be

公式Un()为：

第四行开始的蕴涵符将公式分为两个部分。每个部分的表达式都用方括号括了起来，方括号前有一个或两个存在量词。

最后一行是最容易的部分：它只是简单地声称存在两个数s和t，使得字符S₁（0）出现在纸带t格上的完全格局s中。图灵在第8节证明了，没有任何算法可以告诉我们一台机器是否打印过0，所以我相信你将要看到图灵从天而降的灵感了。

公式Un(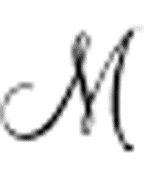)一开始断言存在数u（数字0），它既表示第一个完全格局的数字，也表示第一个扫描格。第一行的其余部分仅仅表明对于每一个x，都有一个x的后继x′。

第二行有点长，但仅简单断言了完全格局u（0）和纸带上的每个格y，y格中符号为S₀或空，这是纸带的初始条件。第三行包含一个I函数，用来说明在完全格局0中扫描格为0；还有一个K函数，用来将初始m-格局设置为q₁。紧跟其后的是描述机器本身的Des(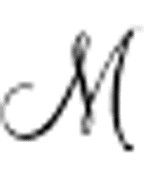)表达式。

从前面的公式中，图灵抽取出方括号中的部分内容，并给出另一个缩写。

[N(u)&…& Des()] many be abbreviated to A().

[N(u)&…& Des()]可以缩写为A()。

命题A(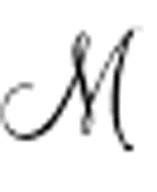)包括了机器的启动条件及对机器的描述，还有一个自由变量u。

在发表的论文修订版中，图灵注意到了隐含在这一证明下的问题，我在第12章也讨论了这个问题。他并没有证明后继是唯一的。因此，他定义了命题函数G(x, y)，它在y大于x时为真，以及表达式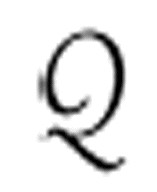，用来代替皮亚诺公理的P。

是下列表达式的缩写：

这个定义中采用了自然数，这使得简写A(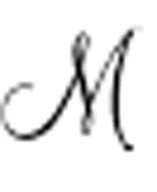)变得更加简单。这是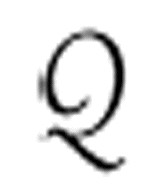、机器启动条件和机器描述的合取。

A()是下式的缩写：

在A(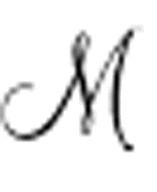)中，u是个自由变量，这个变量在Un(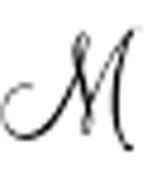)公式中就有约束了：

Un()是下式的缩写：

我去除了谓词N(x)，因为所有这些命题函数的定义域都隐含假定为自然数。根据谓词R、I、K和F的定义以及公式Inst和Des，图灵说：

When we substitute the meanings suggested on p. 259-60 we find that Un () has the interpretation “in some complete configuration of , S₁ (i.e. 0) appears on the tape”.

当我们采用第259～260页暗示的含义时，会发现Un()可以解释为“在的某个完全格局中，S₁（也就是0）出现在纸带上”。

因为在Un(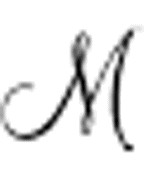)中，蕴涵符左侧的表达式包括了对机器的描述和启动条件，我们假设它为真，它们就是公理。蕴涵符右侧是一个表达式，当机器在运行期间打印了0时为真。因此，如果公式Un(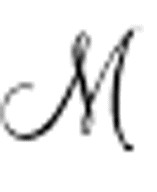)右侧为真，也就是说机器打印了0，那么其本身也为真；如果机器从未打印0则为假。是否存在一个算法可以确定Un(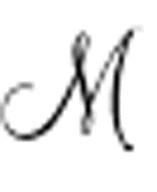)是否可证明？如果存在，那么同样也存在一个算法告诉我们任意一台机器是否打印了0。

注意，图灵使用了“暗示的”命题函数的含义。接下来的大部分证明将基于对公式的纯粹句法解释，而不需要我们考虑这些函数的准确含义。

现在，图灵想证明Un(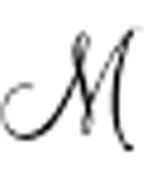)是可证明的，当且仅当S₁出现在纸带上。他将证明分为两部分，每一部分使用两个引理（辅助的证明），他称之为引理1和引理2，但一开始引理以(a)和(b)命名。

Corresponding to this I prove that

(a) If S₁ appears on the tape in some complete configuration of , then Un() is provable.

(b) If Un() is provable, then S₁ appears on the tape in some complete configuration of .

When this has been done, the remainder of the theorem is trivial.

与之对应，我将证明

(a) 如果S₁出现在的某个完全格局下的纸带上，那么Un()是可证明的。

(b) 如果Un()是可证明的，那么S₁出现在的某个完全格局下的纸带上。

完成这些证明之后，定理的其余部分就很简单了。

比较难的是引理1，图灵又逐字重复了一遍。

[261]

LEMMA 1. If S₁ appears on the tape in some complete configuration of , then Un() is provable.

We have to show how to prove Un().

引理1 如果S₁出现在的某个完全格局下的纸带上，那么Un()是可证明的。

我们必须说明如何证明Un()。

和之前一样，u是我们通常所知的0，u′是1，u″是2，u⁽ⁿ⁾的意思是u的右上角有n个撇，表示数字n。

另外，图灵在论文的下一句中引入了一些新的记号，包括3个新函数r(n, m)、i(n)和k(n)。这些函数不是命题函数，因为它们返回整数。参数n是一个完全格局，参数m代表纸带上的方格。

函数r(n, m)返回在完全格局n中出现在m格上的字符的索引。索引为0代表空格，1代表0，2代表1，等等，因此S_{r(n, m)}代表在完全格局n中出现在m格上的字符。图灵将把这个以r函数为下标的S与命题函数R相结合：

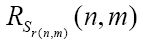
这个谓词永远为真，图灵将使用含上标的u来表示R的参数：

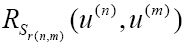
图灵允许在r函数中使用n和m，但是R谓词中必须包含u⁽ⁿ⁾和u^(m)。

图灵引入的第二个新函数是i(n)，它返回在完全格局n下扫描格的数目，因此谓词：

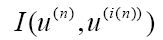
总为真，因为它指的是完全格局n和扫描格i(n)。第三个新函数k(n)返回完全格局n中m-格局的索引，因此q_k(n)就是完全格局n中的m-格局。谓词：

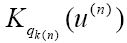
总为真，因为它表明在完全格局n中，m-格局为q_k(n)。

Let us suppose that in the n-th complete configuration the sequence of symbols on the tape is S_{r(n, 0)}, S_{r(n, 1)},…,S_{r(n, n)}, followed by nothing but blanks, and that the scanned symbol is the i(n)-th, that the m-configuration is q_k(n).

我们假设在第n个完全格局中，纸带上的符号序列为S_r(n,0), S_r(n,1)，… S_r(n,n), 后面都是空格，并且扫描符是第i(n)个，m-格局为q_k(n)。

在完全格局0中，纸带是完全空白的。完全格局1中，可能有一个非空的符号出现在纸带上。总体而言，对于完全格局n，最多有n个符号出现在纸带上（很可能更少）。图灵将这个从第0格开始的符号序列表示为S_r(n,0), S_r(n,1),…S_r(n,n)。如果他实际列出的是n+1个字符而不是n个，这也没有问题，因为某些r函数无疑会返回0，从而指示的是空格。

Then we may form the proposition

which we may abbreviate to CC_n.

那么我们可以构造这样的命题：

我们将其缩写为CC_n。

这其实就是“完全格局n”。第一行包括了对应于前n+1个方格中符号的函数的合取，第二行包含了涉及扫描格i(n)和m-格局q_k (n)的函数。

第三行开始，紧跟在全称量词后面的F应该在大括号里面。正如第一行表明了出现在纸带上编号从0至第n格的符号，最后一行表明了编号大于n的格只包含空格。R谓词出现在最后。全称量词y针对纸带上的所有方格。要么u′是y格的后继（即y为0），要么y格是u的后继（即y是1），或者y是u′的后继（即y为2），等等，一直推导到y是n-1的后继（即y是n）。如果y不是上面几种情况中的一种，那么y格包含的是空格。

下面是修正后的版本。

CC_n是下面表达式的简写：

当n等于0时，第一行及第三行的大部分就会消失。CC₀是下面表达式的缩写：

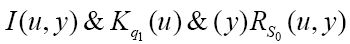
As before, F(u, u′) & F(u′, u″) &…& F(u^(r-1), u^(r)) is abbreviated to F^(r).

I shall show that all formulae of the form A() & F⁽ⁿ⁾ → CC_n (abbrevated to CF_n) are provable.

同前一样， F(u, u′)&F(u′, u″)&…&F(u^(r-1),u^(r)) 缩写为F^(r)。

我会说明所有形如A() & F⁽ⁿ⁾→CC_n（缩写成CF_n）的公式都是可证明的。

对于A()公式，你可能会想起，它结合了机器的启动条件（一条空白的纸带，m-格局为q₁，编号为0的扫描格）及Des(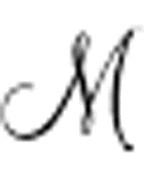)表达式，后者是机器的说明。Des(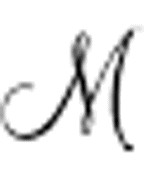)表达式包括了多个指令表达式，每个指令表达式都说明了指令如何改变了扫描格上的符号，改变了m-格局，改变了将要扫描的方格。

图灵为每个完全格局n定义了一个称为CF_n的公式。

CF_n为下面公式的缩写：

下面是CF_n的前几个公式：

…

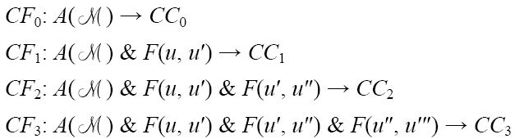
The meaning of CF_n is “The n-th complete configuration of is so and so” where “so and so” stands for the actual n-th complete configuration of . That CF_n should be probable is therefore to be expected.

CF_n的意思是“的第n个完全格局是这样的”，其中“这样” 指的是实际的第n个完全格局。因此，我们可以期待CF_n是可证明的。

图灵用归纳法来说明CF_n公式是可证明的。他首先证明了CF₀是可证明的，接着说明如果CF_n是可以证明的，则CF_n+1也是可证明的。

CF₀ is certainly provable, for in the complete configuration the symbols are all blanks the m-configuration is q₁, and the scanned square is u, i.e. CC₀ is

CF₀当然是可证明的，因为在完全格局中，所有符号都是空格，m-格局为q₁，扫描格为u，即CC₀是

这是公式CC₀的一个重新排列后的版本，我之前也展示过。A(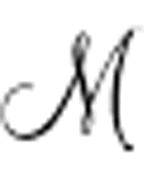)的表达式为：

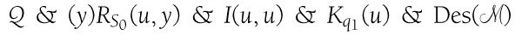
A(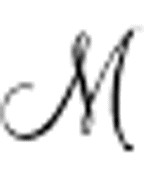)包含了与CC₀完全相同的谓词R、I和K。

A) → CC₀ is then trivial.

We next show that CF_n → CF_n+1 is provable for each n.

然后易得A() → CC₀。

下面我们证明对于任何n， CF_n → CF_n+1是可证明的。

看一下CF_n的表达式，可以发现

CF_n → CF_n+1

是下面公式的缩写：

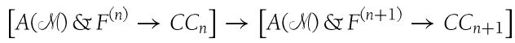
这里是归纳证明比较难的部分，但是如果证明了这个蕴涵关系，我们就可以说CF₀ → CF₁是可证明的，CF₁ → CF₂是可证明的，以此推理可知，所有的CF_n表达式都是可证明的。

There are three cases to consider, according as in the move from the n-th to the (n + 1)-th configruation the machine moves to left or to right or remains stationary. We suppose that the first case applies, i.e. the machine moves to the left. A similar argument applies in the other cases.

在从第n个格局转换至第n+1个格局时需要考虑三种情形：机器是向左移动、向右移动还是保持静止。我们假设是第一种情形，即机器向左移动。对其他情形，类似的论据也成立。

下句话的前一部分，图灵基于之前定义的函数r、i和k定义了整数a、b、c和d。但是，这些定义有些混在一起了。

If r(n, i(n)) = a, r(n + 1, i(n+1)) = c, k(i(n)) = b, and k(i(n + 1)) + d,

如果

r(n, i(n))=a，r(n+1, i(n+1))=c，k(i(n))＝b并且k(i(n+1))＝d，

在图灵发表的论文修订版中，他解释了这些定义，这些都跟完全格局n有关：

a = k(n)，m-格局的索引

b = r(n, i(n))，扫描格i(n)中符号的索引

c = k(n+1)，下一个m-格局的索引

d = r(n+1, i(n))，扫描格i(n)中新符号的索引

a和c是q的下标；b和d则是S的下标，这些缩写仅仅是为了简化剩余的表达式和接下来的一些条目。

then Des must include Inst {q_a S_b S_d L q_c} as one of its terms, i.e.

Des) → Inst{q_a S_b S_d L q_c}.

那么Des()一定包含指令{q_aS_bS_dLq_c}作为其中一项，即

Des() → Inst{q_a S_b S_d L q_c}

因为Des由所有Inst指令的合取组成，因此如果Des为真，那么所有单独的Inst指令也为真，上述蕴涵关系也就成立。A(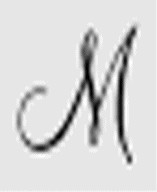)是Des和其他表达式的合取，因而

A(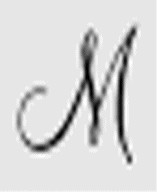) → Des()

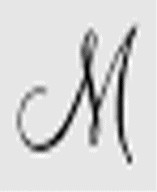结合这两个蕴涵关系，我们可以得到：

A(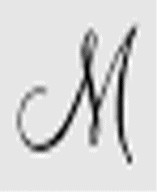)→ Inst{q_aS_bS_dLq_c}

表达式F⁽ⁿ⁺¹⁾是F谓词合取的缩写，这些F谓词同样也假设为公理。因为F⁽ⁿ⁺¹⁾为真，所以我们可以把它以合取形式加到公式的两边。

Hence

But

is provable,

因此

而 是可证明的,

这里需要修正一下：左侧的合取必须包括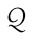，用来保证后继的唯一性：

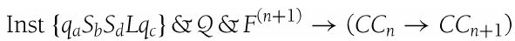
如果把Inst表达式中的下标a、b、c和d替换掉，将得到一个特别的Inst指令，它使得完全格局n前进至完全格局(n+1)。

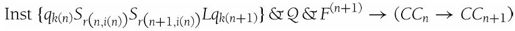
这个公式等价于

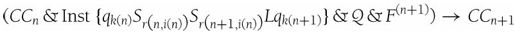
直观上看这很明显：特别的Inst指令使CC_n前进到CC_n+1，而CC_n+1可以由CC_n与这一指令的合取得到。但是，要通过对相关的命题函数进行操作来说明这是可证明的，将是非常繁琐的，因为Inst和CC_n缩写都非常复杂。

图灵刚刚提出的两个命题是可证明的，

and so therefore is

因此

这是X → (Y → Z)形式的命题，很容易说明这与X → (Y → Z)等价，因此：

回想一下，带上标的F是F谓词合取的缩写，因此F^{(n+1) →} F⁽ⁿ⁾且。

[262]

and

并且

这两个括号中的表达式都能表示成CF_n缩写形式。

i.e.

CF_n → CF_n+1.

CF_n is probable for each n.

即CF_n→CF_n+1。

对于每个n，CF_n都是可证明的。

至此，给出了说明CF_n是可证明的归纳证明，但我们还没有完成引理的证明，因为我们真正需要证明的是Un()。

Now it is the assumption of this lemma that S₁ appears somewhere, in some complete configuration, in the sequence of symbols printed by ; that is, for some integers N, K,

现在根据引理假设，S₁在某些完全格局中出现在所打印的符号序列的某处，也就是说，对某些整数N、K，

这里N是完全格局的序号，K是纸带上的方格，

CC_N has R_S1 (u^(N), u^(K)) as one of its terms, and therefore CC_N → R_S1 (u^(N), u^(K) is provable.

R_S1 (u(^N), u^(K) 是 CC_N 中的一项，因此CC_N → R_S1 (u^(N), u^(K))是可证明的。

这个成立是因为合取式中任意一项都能推出该项成立。

We have then

and

那么我们可以得到

并且

CC的上标应该是下标，这是CF_N的定义，图灵刚刚证明了CF_N对于所有的N都可证明（尽管之前他用的是小写的n，而不是大写的N）。

到目前为止，图灵一直在处理包含自由变量u的公式。

We also have

where N′ = max (N, K).

我们同样有

其中 N’ = max(N，K)。

实际上，K（指纸带上出现0的方格）永远不可能比N（完全格局）大，因此N’总是等于N。右侧的表达式A() & F^(N)只是为了推导出CC_N，我们刚刚证明了CC_N可以推导出 R_S1 (u^(N), u^(K))。

And so

因此

R函数并不要求从u至u^(N′)的所有整数都存在，仅仅需要u^(N)和u^(K)存在即可。因此大部分存在量词都可以去除，剩下的就是：

如果我们用s代替u^(N)，t代替u^(K)，就得到

这恰好就是Un()的定义，你可以在第254页的框中看到。但是，它并不是图灵在其原始论文中对Un()的定义。他之前把N(s)和N(t)写在了蕴涵符右侧的表达式中，但那些谓词仅仅表明s和t是自然数，而我们已经推导出这一事实了。

以“如果S₁出现在的某个完全格局下的纸带上”作为前提，我们刚刚证明了公式Un()。

i.e. Un() is provable.

This completes the proof of Lemma 1.

即Un()是可证明的。

至此，完成了引理1的证明。

第二个引理的证明更简短，只需要使用之前定义的命题函数来解释这个公式。

LEMMA 2. If Un( is provable, then S₁ appears on the tape in some complete configuration of .

If we substitute any propositional functions for function variables in a provable formula, we obtain a true proposition. In particular, if we substitute the meanings tabulated on pp. 257-260 in Un (), we obtain a true proposition with the meaning “S₁ appears somewhere on the tape in some complete configuration of ".

引理2 如果Un()是可证明的，那么S₁出现在M的某个完全格局下的纸带上。

如果我们在可证明的公式中用任意命题函数来代替函数变量，那么就会得到一个真命题。特别地，如果我们采用含义“S₁出现在的某个完全格局下的纸带上”而非第259~260页的Un()中的含义，就能得到一个真命题。

现在，图灵已经证明，Un()可证明当且仅当 S₁出现在机器的某个完全格局下的纸带上。

We are now in a position to show that the Entscheidungsproblem cannot be solved. Let us suppose the contrary. Then there is a general (mechanical) process for determining whether Un() is provable. By Lemmas 1 and 2, this implies that there is a process for determining whether ever prints 0, and this is impossible, by § 8. Hence the Entscheidungsproblem cannot be solved.

我们现在来证明判定性问题不可解。先假设其否定命题成立，那么就存在一个通用（机械）过程可以判定Un()是否可证明。根据引理1和引理2，这表明存在一个过程可以确定机器是否打印了0，但这在§8中已经提及是不可能的。因此判定性问题不可解。

回想一下，这很简单，你同意吧？

Un()是个相当复杂的公式，这一点也不奇怪。如果它比较简单，那么它就可能会被判定过程分析。相反，Un()中包含了A()，A()中包含了Q和Des()，Des()还是组成机器的所有Inst项的合取。每个Inst项有五个全称量词，Q包含三个全称量词和一个存在量词，A()包含另一个全称量词，Un()含有三个存在量词。

如果这个复杂的量词嵌套中仅包含一元谓词，也就是说，谓词中仅含一个参数，那么它不会影响命题的可解性。1915年，利奥波德·勒文海姆（1878—1957）证明了仅包含一元谓词的命题是可判定的。^［2］

到图灵写这篇论文时，人们在为特殊情形的公式寻找判定过程方面已经取得了许多进展。通常，应用判定过程时，公式一般首先转换为前束范式，也就是，通过改变公式让所有（非否定形式）的量词都可以移到公式的开始处，位于一个称为“矩阵”的不含任何量词的表达式之前。

在那些年里，许多数学家已经发现了前束范式形式的很多类公式的判定过程，它们都是以一个特殊形式的量词开头。在有关判定性问题的文献中^［3］，都是使用和符号表示全称量词和存在量词。上标的数字代表了一个特定量词的数目，星号可以是任何数字。

1928年，保罗·贝奈斯和摩西·施隆芬克尔（1889—1942）发表了以 （任意数量的存在量词，后跟任意数量的全称量词）开头的命题的判定过程。同样在1928年，威廉·阿克曼给出了的判定过程（任意数量存在量词后跟一个全称量词，再接任意数量的存在量词）。1932年，哥德尔给出了任意数量的存在量词间包含两个全称量词的判定过程： 。

人们还探索了与判定性问题相联系的一类问题：化简类。化简类由所有以特定量词模式开头的命题组成，仅当所有命题都存在判定过程，各种化简类中的命题存在判定过程。1920年，斯科莱姆证明定义了一个化简类。1933年，哥德尔将范围缩小到。

在图灵和邱奇的证明之前，化简类是否存在判定过程是未知的，仅仅知道如果存在一个化简类的判定过程，那么也会存在一个通用判定过程。图灵和邱奇的论文的结果表明，这些化简类是不可判定的。1932年，哥德尔给出了一个以为前缀的命题的判定程序，并将其推广到。在图灵的证明出现之后，我们可知任何以为前缀的命题是不可判定的。通过增加一个全称量词，形为的可判定命题变成了形为的不可判定命题。

在下面的段落中，图灵使用quantor代表量词。

In view of the large number of particular cases of solutions of the Entscheidungsproblem for formulae with restricted systems of quantors, it

[263]

is interesting to express Un() in a form in which all quantors are at the beginning. Un() is, in fact, expressible in the form

(I)

where contains no quantors, and n = 6.

对于带受限量词（quantor）的公式的判定性问题的一大类特殊情形的解，把Un()表示成所有的量词都出现在开始处，这会比较有趣。事实上，Un()可以表示成

(I)

其中不包含任何量词，并且n = 6。

图灵已经证明以（使用约定俗成的定义）为前缀的命题构成了一个化简类。带有此类前缀的命题不存在判定过程。

By unimportant modifications we can obtain a formula, with all essential properties of Un(), which is of form (I) with n = 5.

通过改变一些不重要的地方，我们可以得到一个包含所有Un()必要性质的公式，形式与(I)相同，但n = 5。

在图灵论文的修订版中，图灵标注出这个数字应该是4，因此化简类被进一步限制到。

1962年，瑞士逻辑学家朱利叶斯·理查德·步琪（1924—1984）利用图灵机从另一方面着手研究判定性问题，并且成功地使证明简化了一点。^［4］ 他的研究表明，形式的命题形成的是化简类。（这类命题是两个项的合取，每一项都将自身的量词置于最前面。）步琪的论文同时为证明命题形成化简类奠定了基础，这意味着即使对于以为前缀的简单命题都不存在通用判定过程。

数学家们发明解决问题的方法惠及了整个世界，当他们证明了某个问题无解时也能起到同样的效果。就如无法仅用尺和圆规三等分一个角，无法求与已知圆面积相等的正方形，无法证明能从欧几里得的前四个公设推导出第五个。对于n大于2的情况，方程xⁿ + yⁿ = zⁿ 没有整数解，无法在系统中建立算术的一致性，以及一阶逻辑没有通用判定过程。

我们可以不再把时间浪费在一个无法做到事情上。知道什么不可能与知道什么可能同样重要。