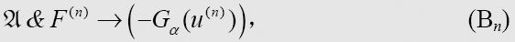1958年夏天,中国出生的逻辑学家王浩利用他在牛津大学教学工作的休假时间,来到坐落于纽约州波基普西市的IBM研究实验室,操作当时最先进的IBM 704计算机。他在IBM的打孔卡片上编码了几乎半个世纪前由阿尔弗雷德·诺斯·怀特海和伯特兰·罗素合著的巨著《数学原理》中的定理。例如,定理*11.26在《数学原理》中的符号表示是:
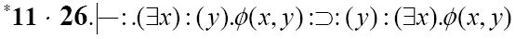
王浩在打孔卡片上,将它写成:
11*26/EXAYGXY-AYEXGXY
他还写了三个程序来读取这些卡片的内容,并且通过应用各种等式和将这些陈述转换成公理的推理规则来证明被编码的定理。这些程序的大部分时间都用在读取卡片内容和打印证明步骤的机械过程上。据他估计,证明《数学原理》第1章到第5章的220条定理的实际处理时间不超过三分钟。他后来提出的第三个程序改进版本能在大约四分钟内证明第9章到第13章的158条定理。[1]
王浩的程序并不是使用计算机进行定理证明的首次尝试。[2]1954年,马丁·戴维斯就使用普林斯顿高等研究院建造的计算机,编写了一个简单的、只包含加法的Presburger算术程序。这是目前已知的第一个由计算机给出的数学证明。戴维斯的这个程序证明了,两个偶数的和仍然是一个偶数。[3]
1957年,艾伦·纽厄尔、约翰·肖和赫伯特·西蒙发表了由他们编写的称为“逻辑理论机器”的程序运行结果,它是为兰德公司制造的JOHNNIAC计算机编写的,这台计算机的命名是为了纪念约翰·冯·诺依曼。[4]他们也使用《数学原理》作为定理的来源。相对于数学逻辑,他们对人工智能更感兴趣,因此编写程序来模拟人证明定理时采用的方法(他们称之为“启发式”的方法)。王浩后来探索的是一种更加算法化的方法,它的效率更高,成功率也更高。
逻辑理论机器的结果是以信件形式通知伯特兰·罗素的,据说他回复道:“得知《数学原理》现在可以采取机械方式来完成,我很高兴。要是我和怀特海早知道能这么做,就不用浪费十年的时间来手工完成了。”[5]
《数学原理》有三卷,约2000页,在数学和逻辑领域都是了不起的成就。在现代文库列举的20世纪一百部最佳非小说类著作中,《数学原理》名列第23。[6]然而,极少有人真的能够下决心阅读这本书。斯蒂芬·克莱尼是阿隆佐·邱奇的学生,后来撰写了《数学概论》(1952)和《数理逻辑》(1967),他坦言自己从来没有读过《数学原理》。[7]在那些自1913年来在数理逻辑领域做出贡献的人中,像他这样的人可能占大多数。
《数学原理》的引言只陈述了一个目标,那就是“完整地列举出数学推理的所有方法和步骤”,这就是我们所熟悉的称为逻辑主义的纲领(也是一种数学哲学),逻辑主义是指把逻辑作为数学其他部分的基础。为了实现这个目标,怀特海和罗素采用了一整套的集合理论和逻辑工具,他们有意限定数学技巧的做法在当时看起来是很荒诞的。
大卫·希尔伯特却不这么认为,他将称为形式主义的数学哲学更紧密地联系在一起。形式主义着重公理化理论,特别是在希尔伯特的纲领中,它更多地强调了诸如一致性、稳定性、完备性和可判定性的概念。
大卫·希尔伯特把《数学原理》的逻辑分解成一个个扩展的子集,并且每个子集都可以单独拿来研究。他这样做一方面是为了教学,另一方面也是为了便于分析。1917年冬天至1918年,他在哥廷根以这种方法为基础教授了一门课程。1928年,大卫·希尔伯特和威廉·阿克曼基于该方法,合著了一本120页的书《数理逻辑原理》,这本书通常称为《希尔伯特和阿克曼》,它也是图灵论文的重点——判定性问题——的来源。
图灵在论文中明确指出,他参考了《数理逻辑原理》和《数学基础》。后者是大卫·希尔伯特与保罗·贝奈斯合著的,该书的第一卷于1934年在柏林出版,以《希尔伯特和贝奈斯》著称。(该书的第二卷在1939年图灵的论文发表之后才出版)。
阅读图灵论文的下一部分需要对希尔伯特和阿克曼发展的数理逻辑理论有一定的了解。在接下来对该逻辑的概述中,我将采用图灵使用的记号,这与《希尔伯特和阿克曼》中所使用的记号很相似。我还将模仿把这个逻辑作为特征的扩展子集的方法,这种方法已经成为了一个标准方法,在阿隆佐·邱奇、斯蒂芬·克莱尼、伊里奥特·门德尔森、赫伯特·恩德滕和许多其他数学家关于数理逻辑的教科书中都可以看到。
首先,我要介绍《希尔伯特和阿克曼》中称作Ausssagenkalkul的概念,它后来翻译成句子演算,不过现在更多地称之为命题演算或命题逻辑。
然后,我会把这一逻辑推广到《希尔伯特和阿克曼》中所称的engere Funktionenkalkul(受限的函数演算)。在那本书的第二版(出版于1938年)中,它更名为engere Pradilatenkalkul(受限的谓词演算),现在更多地称之为一阶逻辑、一阶谓词逻辑或一阶谓词演算。介绍完一些概念后,我就可以介绍一阶逻辑和二阶逻辑的区别了。《希尔伯特和阿克曼》最初把二阶逻辑叫做erweiterte Funktionenkalkül,后来称之为erweiterte Prädikatenkalkül(扩展的谓词演算)。
命题(句子)逻辑处理所有具有真值的陈述命题,也就是说,我们可以判定这些命题的真假。例如下面的命题:
今天是星期三。
7是一个素数。
天正在下雨。
我妈妈的名字叫做芭芭拉。
10是完全平方数。
其中,一些为真,一些为假,还有一些可能对于我而言是真,对于你而言则是假的。(不要争论!)在命题逻辑中,每个命题都有一致的真值,没有模棱两可。并且,如果我们不那么自称自己很擅长分析除了数学命题之外的任意其他命题,困惑就会越少。
在命题逻辑中,通常使用斜体大写字母表示语句。字母表中前面的字母,如A、B、C等,通常代表有固定真值的特定命题;而后面的字母,如X、Y、Z等,用来表示变量命题。
我们可以使用某些连接词把单个命题组合成更复杂的命题。
第一个这样的连接词用一个小写字母v表示,它出自拉丁语单词vel,意思是“或”。特别地,“或”又可分为“与或”和与之相对的“异或”(拉丁语aut)。当X或Y中的任意一个为真,或两个均为真时,命题:
X v Y
为真。如下的真值表可以帮助展示X和Y真值的不同组合情况。
| X | Y | X v Y |
| 假 | 假 | 假 |
| 假 | 真 | 真 |
| 真 | 假 | 真 |
| 真 | 真 | 真 |
在不会产生混淆的情况下,允许省略符号v。公式XY等价于X v Y。
注意,我没有使用把两个公式写在同一行并用等号连接的方法来表示这种等价关系。命题演算语言不包含等号,至少在《希尔伯特和阿克曼》制定的命题演算中是不包含的。
我们说一个命题等价于另一个命题,指的是当组成它们的命题有相同的对应真值时这两个命题也有相同的真值。我们使用人类语言或者称为元语言来表达这种等价关系,准确地区分逻辑语言和元语言可以避免混淆。
《希尔伯特和阿克曼》使用元语言缩写aq.(表示德语中的äquivalent)或eq.(表示英语的equivalent)表示等价:
X v Y eq. XY
记住,这个缩写不是命题逻辑语言的一部分,严格意义上只是为了方便才使用它。
“与”的概念用符号&表示。公式
X & Y
为真当且仅当X和Y同时为真,其真值表如下。
| X | Y | X & Y |
| 假 | 假 | 假 |
| 假 | 真 | 假 |
| 真 | 假 | 假 |
| 真 | 真 | 真 |
“与”运算常称为合取(conjuction),这一称呼源于and一词的语法作用。据此,“或”运算常称为析取(disjuncton),这是人们不太熟悉的词。
很明显,从真值表可以得到如下的结论:
X v X eq. X
X & X eq. X
你还可以在一个复合命题中同时使用这两个连接符。在这种情况下,先计算v的值,再计算&的值。你可以使用括号来改变运算顺序,也可以只是为了清晰起见而使用括号。
X & Y v Z eq. X & (Y v Z)
这两个命题都不等价于:
(X & Y) v Z
例如,当X为假,Y为真,Z为真时,前两个命题都为假,而最后的命题却为真。
我就不喋喋不休地介绍那些确保括号总是正确配对,以及连接词应出现在正确位置的各种各样的规则了。这些规则有助于合式公式(well-formed formula,或称为wff,发音是woofs)这一概念的形成。true、false、T和F都不是命题逻辑词汇表中的单词,但是为了方便,你可以使用它们来代替命题字母。可以用T表示一个恒为真的命题,使用F表示一个恒为假的命题。从现在开始,我也会在真值表里使用T和F。
从真值表很容易得到下面的等价关系:
X v T eq. T
X v F eq. X
X & T eq. X
X & F eq. F
很明显,从真值表中也可以看出下面两种运算满足交换律:
X v Y eq. Y v X
X & Y eq. Y & X
下面两种运算满足结合律:
X v (Y v Z) eq. (X v Y) v Z
X & (Y & Z) eq. (X & Y) & Z
下面两种运算满足分配律:
X v (Y & Z) eq. (X v Y) & (X v Z)
X & (Y v Z) eq. (X & Y) v (X & Z)
如果把真值表中的F替换为0,把T替换成1,可以看出,合取运算其实等价于两个一位二进制数的乘积;相应地,析取与加法相似。因此,有时把合取称为“逻辑乘”,把析取称为“逻辑加”。然而,使用这些术语会导致不一致,因此不建议使用它们。
合取和析取都是二元运算。唯一的一元运算称为“非”或“否”,使用类似减号的一划来表示它:
| X | - X |
| F | T |
| T | F |
《希尔伯特和阿克曼》通过在字母或表达式的上方加一个横线表示“非”运算,图灵的标注与他们的不同。否定总是被最先计算,并且否定的符号只作用于紧随其后的符号。两个否定会抵销:
—X eq. X
下面是两个非常基本的等价关系:
X v -X eq. T
X & -X eq. F
两个最基本的、同样也是最有趣的逻辑关系把合取、析取与否定结合了起来。它们以19世纪的数学家奥古斯都·德·摩根(1806—1871)的名字命名,叫做德·摩根定律,尽管这个基本概念在很早之前已经为亚里士多德所了解。
(X v Y) eq. -X & -Y
(X & Y) eq. -X v -Y
用通俗的语言来表达这些等式,其含义是显而易见的。例如,“现在没有下雨或下雪”可以表示成可(X v Y),它的意思是“现在没有下雨,也没有下雪”,后者可以表示成-X & -Y。如果有人告诉我:“你当然不是既富又帅的人。”也就是- (X & Y),我可以得出如下的结论:“我想,我要么贫穷或者丑陋,要么既贫穷又丑陋吧……”这也就是-X v -Y。
注意,可以把德·摩根定律里的否定符号都写在一边,于是它们可以转换成:
X v Y eq. - (-X & -Y)
X & Y eq. - (-X v -Y)
在“与”和“或”运算的真值表中,将“真”都变成“假”,“假”都变成“真”,可以得到相反运算的真值表。我们把它称为“对偶原理”,这同样也适用于复杂的命题。例如,
X & -Y v Z
对所有的符号都变成其相应的否定形式,然后交换&和v(原有隐含需要加括号的地方要记得加括号),得到的新命题就是原来命题的否定形式:
-X v (Y & -Z)
如果你想证明这两个命题确实是彼此否定的,那么可以构造下面的真值表来测试所有的值。
| X | Y | Z | X &-Y v Z | -X v (Y &- Z) |
| F | F | F | F | T |
| F | F | T | F | T |
| F | T | F | F | T |
| F | T | T | F | T |
| T | F | F | T | F |
| T | F | T | T | F |
| T | T | F | F | T |
| T | T | T | T | F |
最后两列的值完全相反,因此,
X & -Y v Z eq. -(-X v (Y & -Z))
没有专门的“异或”运算符,但是可以采用下面的公式实现这个运算:
(X v Y) & - (X & Y)
从下面的真值表可以看出这个命题的工作原理。
| X | Y | X v Y | X & Y | (X v Y)& - (X & Y) |
| F | F | F | F | F |
| F | T | T | F | T |
| T | F | T | F | T |
| T | T | T | T | F |
除了X和Y均为真的情况,“异或”与一般的析取运算类似。
如果把德·摩根定律应用到“异或”的后半个表达式上,可以得到
(X v Y) & (-X v -Y)
你可能更喜欢这种对称的表达形式。
计算机电路使用异或运算计算两个二进制数位的加法,并使用合取运算计算进位。[8]
第三个二元运算有点棘手,它称为蕴涵,你可以把X→Y读作“X蕴涵Y”或“若X为真,则Y为真”。预先警告一下,很多人在看到蕴涵运算的真值表时,会产生“这里有点儿错”的反应。
| X | Y | X → Y |
| F | F | T |
| F | T | T |
| T | F | F |
| T | T | T |
前两条看上去很奇怪。如果X为假,为什么无论Y的值是真是假,X→Y的值都为真呢?一种理解的方法是,首先假设X→Y为真。如果X→Y为真,并且X为真,那么Y一定为真。然而,如果X的值不为真,那么讨论Y的值有什么意义呢?一点意义都没有。Y可以是任意值。这就是为什么X为假的时候,无论Y的值为何,X→Y都为真的原因。
看看这个命题:“如果天下雨,那么水汽凝结。”如果天在下雨,那么这个命题为真;如果天没有下雨,这个命题也为真。该命题只有在天下雨,而水汽又没有凝结的时候才为假。
数理逻辑中经常用到蕴涵式。通常情况下,蕴涵符号的左边是我们已知为真的一个公式。因此,如果我们接下来能够证明命题本身为真,就可以推断蕴涵符号右边的公式为真。
蕴涵不满足交换律和结合律。然而,
X → Y eq. -Y → -X
我们称第二个命题为反命题。如果天在下雨,那么我会打伞。如果我没有打伞,那么肯定没有下雨。蕴涵和析取之间有一个简单的关系:
X → Y eq. -X v Y
换句话说,如果X为假,或者Y为真,那么X → Y为真。同样,也可以使用合取运算来表示蕴涵:
X → Y eq. - (X & -Y)
如果蕴涵符号的左边是任意多个命题的合取式,那么这些命题中的任何一个都可以放在蕴涵符号的右边:
X & Y → X
X & Y → Y
《希尔伯特和阿克曼》描述了一个双条件(即“当且仅当”)运算,并且用一个波浪号表示:
| X | Y | X ~ Y |
| F | F | T |
| F | T | F |
| T | F | F |
| T | T | T |
X ~ Y为真,当且仅当X和Y的真值相同。图灵在其论文中没有使用这个双条件运算。然而,它等价于两个方向相反的蕴涵式的合取式,这一结论是有意义的。
X ~ Y eq. (X Y)&(Y → X)
如果你认可这样的等价关系是有意义的,那么只有当T→T为真(我们都认可)并且F→F也为真(这个未确定)时它才能起作用。同样,T→F和F→T的真值必须相反。我们都同意T→F必然为假,这也意味着F→T必须为真。这证实了蕴涵运算的真值表的正确性。
假设我给出如下的命题:
X v Y v (-X &-Y)
你能告诉我什么?为真还是为假?你可能会拒绝说,除非你知道X和Y的值,否则判定不了这个命题的真假。接着,我会建议你建立一个真值表来检测所有X和Y的值的组合。这个表如下:
| X | Y | X v Y v (-X & -Y) |
| F | F | T |
| F | T | T |
| T | F | T |
| T | T | T |
无论X和Y各自什么取值,这个命题总为真。我们把这样的命题叫做重言式,或者说它是永真的。永真命题在数理逻辑中很受欢迎,因为无论单个命题的真值为何,它们的值总为真。
我们来看看另一类命题:
| X | Y | X & Y & -X |
| F | F | F |
| F | T | F |
| T | F | F |
| T | T | F |
这个命题永不为真,这类命题叫做矛盾式。重言式的否定就是矛盾式,而矛盾式的否定就是重言式。
下面是第三个例子:
| X | Y | X v (Y & -Y) |
| F | F | F |
| F | T | F |
| T | F | T |
| T | T | T |
这个命题的值随着X和Y真值的变化,有时为真,有时为假。我们称这类命题为可满足式,指在原子命题真值的某种组合情况下,这类命题的真值可以为真。
永真命题(重言式)也被认为是可满足的。一个命题永真当且仅当这个命题的否定是不可满足的。
对任意一个命题,我们都可以使用真值表来判断它是重言式、矛盾式或者只是可满足式。求真值表的过程是机械的,它不需要任何特别的灵感、洞察力或直觉。如果你是一个计算机程序员,很容易就可以想到编写一段程序,读取命题逻辑中的一个命题,计算它,然后输出词语“重言式”、“矛盾式”或“可满足式”。
基于这一原因,我们说命题演算中的命题是可判定的。存在这样的一个判定步骤,来判定命题逻辑的任一命题的正确性或可满足性。
换句话说,命题演算的判定性问题已经解决了,今天我们都可以早点结束工作回家休息了。
但这并不能说明,真值表总是可行的。假设一个命题中包含100个命题变量,真值表的行数就长达2100,也就是1267650600228229401496703205376,约1030,这是一个非常大的数。即使使用未来处理一行仅需一纳秒(一秒的十亿分之一,也即光传播约一英尺所需的时间)的计算机,处理整个真值表的时间也将长达38万亿年,大约相当于宇宙当前年龄的3000倍。
有一个好消息:如果你把命题限制到55个命题变量,仍然做到一纳秒处理一行,那么整个处理过程只需一年的时间。每增加一个新的变量都会让处理时间加倍。在可计算性和复杂性理论中,处理真值表的计算时间是指数级的,因为它与问题大小成指数相关。
由于这些原因,在判定命题逻辑中命题真假时,解法比真值表更有价值。这些技术通常包括把命题表示成范式,这些范式可以是若干个变元构成的析取项的合取,或者是若干个变元构成的合取项的析取。
这就结束了我对于命题逻辑的匆匆的概述。我们必须继续讨论下去,因为命题逻辑对于许多目的而言还不够充分。它的最大问题就是,我们一直在处理整句的陈述命题,而不能把不同命题的本质联系起来。命题逻辑不能成功地分析亚里士多德的三段论(“所有的人都是凡人;苏格拉底是一个人;因此……”)和刘易斯·卡罗尔设想的简单的连锁推理(“爱吃鱼的猫都是可驯的;没有尾巴的猫都不和大猩猩一起玩;有胡须的猫都爱吃鱼;不可训的猫都是绿眼睛的;有胡须的猫才有尾巴;因此……”[9])。
通过引入命题函数或谓词(图灵喜欢使用前者,如今后者更流行,我将交替使用这两个术语),可以使逻辑的力量更加强大。谓词这个术语出自于语法,从语法的角度看,可以把一个句子分成主语和谓语。例如,在“警察说出了大实话”这句话中,主语是“警察”,谓语是“说出了大实话”。
引入谓词是将命题逻辑转化为一阶谓词逻辑的第一步。无论我们何时使用谓词,都是想把自己限制在一个特定的域或总体中。在现实生活中,这个域通常是指自然数,把其中的个体作为谓词的参数。
在《希尔伯特和阿克曼》中(图灵论文中也是),谓词看起来很像函数,但它的取值只有真和假。我喜欢用整个单词或多个单词来命名谓词,比如IsPrime。谓词IsPrime的域是由自然数组成的,因此IsPrime(7)的值为真,IsPrime(9)的值为假。可以用小写字母表示这个域中的个体,作为变量使用,如IsPrime(x)。
谓词可以包含多个参数。假设现在的域是由你的朋友组成的,他们每个人都有独一无二的名字。当某x爱上某y,谓词Loves(x, y)为真。例如,Loves(Pat, Terry)与命题“Pat爱上Terry”相同。有些谓词中的参数是可以交换的,不过这个命题的谓词不能交换,因此Loves(Pat, Terry)和Loves(Terry, Pat)不同。
我们可以使用与命题逻辑中相同的连接词来连接谓词。如果他们彼此相爱,则下面的命题:
Loves(Pat, Terry) & Loves(Terry, Pat)
为真。如果他们的感情(无论是什么样的感情)是相互的,则命题
Loves(Pat, Terry) ~ Loves(Terry, Pat)
为真。
下面这个命题又是什么意思呢?
Loves(x, Pat)
表达的意思不是完全清楚。如果这个命题确实有某种含义,我们可以猜测,它表示每个人都爱Pat,也有可能是至少有某个人爱Pat。
为了避免这样的二义性,我们必须同时引入两个量词(quantifier,图灵称之为quantors)。第一个是全称量词,它由置于谓词前、括在括号里的变量组成,形式如下:
(x)Loves(x, Pat)
括号中的x表示“对于所有的x”。如果“对于所有的x,x都爱Pat”,那么上式为真,也就是每个人都爱Pat时,命题为真。如果Pat爱每一个人,那么公式
(x)Loves(Pat, x)
为真。我们经常使用符号符表示全称量词,不过《希尔伯特和阿克曼》以及图灵的论文中都没有采用这种记号。
第二种量词是存在量词,可以翻译为“存在”。《希尔伯特和阿克曼》中使用一个正规的字母E来表示存在量词,不过图灵更喜欢使用较为常见的表示方式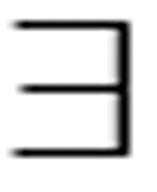 。例如,
。例如,
( x)Loves(x, Terry)
x)Loves(x, Terry)
表示“存在这样的一个x,x爱Terry”,或者说某个人爱Terry,至少有一个这样的人,哪怕这个人就是Terry。
在一阶逻辑(《希尔伯特和阿克曼》中称作“狭义演算”)中,量词只用来修饰表示域中个体的变量。在二阶逻辑(即“广义演算”)中,量词可以修饰代表命题函数的变量。图灵的论文只涉及一阶逻辑。
如果我们处理的是一个有限总体,那么可以把全称量词表示成一个合取式,而把存在量词表示成一个析取式。例如,假设我们的总体由Pat、Terry和Kim组成,则下式
(x)Loves(Kim, x)
等价于如下的合取式:
Loves(Kim, Pat) & Loves(Kim, Terry) & Loves(Kim, Kim)
所有的个体谓词必须都为真时,整个命题的值才为真。公式
(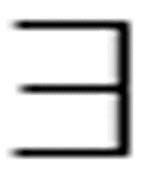 x)Loves(Kim, x)
x)Loves(Kim, x)
等价于:
Loves(Kim, Pat) v Loves(Kim, Terry) v Loves(Kim, Kim)
只要其中的一个谓词为真,就可以使得整个命题的值为真。
回想一下德·摩根定律的对偶性,并把它应用到这两个公式中,你就会发现,当引入否定命题时,全称量词和存在量词彼此可以相互转换,你不必对此过分惊讶。例如,如果不是每个人都爱Terry,那么下面两个等价的公式均为真:
- (x)Loves(x, Terry) eq. (
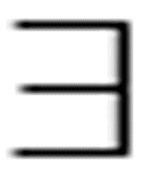 x)-Loves(x, Terry)
x)-Loves(x, Terry)
如果没有人爱Terry,则下面的两个公式均为真:
(x) -Loves(x, Terry) eq. - (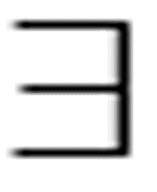 x) Loves(x, Terry)
x) Loves(x, Terry)
类似地,
(x) Loves(x, Terry) eq. - (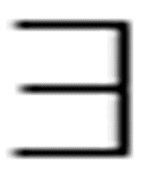 x) -Loves(x, Terry)
x) -Loves(x, Terry)
右边的公式可以解释成:“不存在有人不爱Terry的情况。”与此类似,
(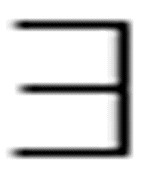 x) Loves(x, Terry) eq. - (x) -Loves(x, Terry)
x) Loves(x, Terry) eq. - (x) -Loves(x, Terry)
意思是,不存在没有人爱Terry的情况。
美国数学家查尔斯·桑德斯·皮尔斯(1839—1914)在研究逻辑量词理论的时候,使用符号Σ(通常与求和相关)表示存在量词,使用Π(通常与求乘积相关)符号表示全称量词。这些表示方法进一步强调了逻辑和二进制运算之间的联系。
由于这些公式中使用到的x都被某个量词修饰,因此称之为约束变量,其作用相当于可变的函数参数。任何不是全称量词或存在量词一部分的变量都是自由变量。在下面的公式中,x是约束变量,y是自由变量:
(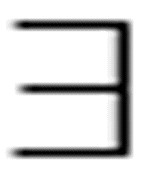 x)Loves(x, y)
x)Loves(x, y)
只要不与其他的变量相冲突,自由变量和约束变量都是可以改变的。例如,我们可以把先前公式中的x改成z:
(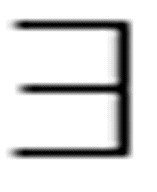 z)Loves(z, y)
z)Loves(z, y)
这个公式与之前的公式表达完全相同的意思,但是,我们不能把这个约束变量变成y,因为y会与自由变量的y冲突,改变后它将变得完全不同。
同一个公式中不能包含两个命名相同的约束变量和自由变量。我们把一阶逻辑中不包含任何自由变量的公式称作命题。使用“命题”一词来描述包含自由变量的公式是不恰当的。
约束变量是有作用范围的,通常用括号来指示。在下面的命题中,x受约束于括号中的整个表达式范围:
(x)[Loves(x, Kim) & Loves(x, Pat)]
注意,这里使用的是方括号而不是圆括号,只是为了使得整个语句可读性更强。这个命题的意思是:每个人都爱Kim和Pat。它和
(x)Loves(x, Kim) & (x) Loves(x, Pat)
意思相同。现在,这两个约束变量相互独立,可以改变其中一个的名字:
(y) Loves(y, Kim) & (x) Loves(x, Pat)
如果某个人既爱Kim又爱Pat,那么命题
(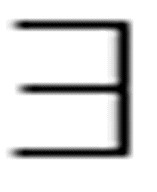 x)[ Loves(x, Kim) & Loves(x, Pat)]
x)[ Loves(x, Kim) & Loves(x, Pat)]
的值为真。然而,如果把这两个谓词分开,意思就会改变。
( x) Loves(x, Kim) & (
x) Loves(x, Kim) & (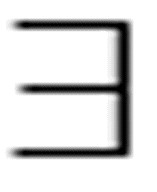 x) Loves(x, Pat)
x) Loves(x, Pat)
现在,如果有某个人爱Kim,并且有某个人爱Pat,则命题为真,这两个人未必是同一个人。
现在把前面几个公式中的合取替换成析取:
(x)[ Loves(x, Kim) v Loves(x, Pat)]
如果每个人或者爱Kim,或者爱Pat(或者既爱Kim也爱Pat),则该命题的值为真。如果Terry爱Kim但不爱Pat,或者Terry爱Pat但不爱Kim,命题也均为真。把两个谓词分开以后,命题的意思会发生变化:
(x) Loves(x, Kim) v (x) Loves(x, Pat)
只有当每个人都爱Kim,或者每个人都爱Pat,或者每个人都爱这两个人的时候,命题才为真。
下面是一个把存在量词应用到析取式中的例子:
(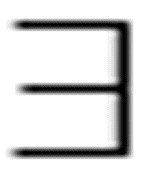 x)[ Loves(x, Kim) v Loves(x, Pat)]
x)[ Loves(x, Kim) v Loves(x, Pat)]
它表示存在某个人爱Kim,或爱Pat,或者同时爱这两个人。把这两个谓词分开后,命题的意思保持不变:
(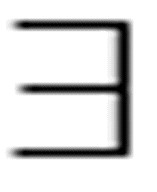 x)Loves(x, Kim) v (
x)Loves(x, Kim) v (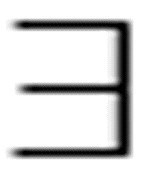 x) Loves(x, Pat)
x) Loves(x, Pat)
下面两个基本的关系适用于所有的命题函数。在这两个例子中,A是谓词,a是定义域中的一个元素。第一个关系是:
(x)A(x) → A(a)
如果这个谓词对定义域中的所有元素都为真,那么它对任意个体的值均为真。第二个关系如下:
A(a) → (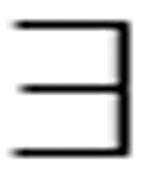 x)A(x)
x)A(x)
几个量词可以一起使用。例如,
(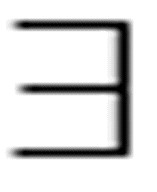 x)(y)Loves(x, y)
x)(y)Loves(x, y)
它表达的意思与把量词按如下方法组织在一起所表达的意思相同:
(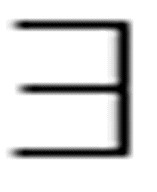 x)[(y)Loves(x, y)]
x)[(y)Loves(x, y)]
如果存在某个人爱所有的人,则该命题为真。改变量词的顺序,表达的意思就不大一样了:
(y) ( x) Loves(x, y)
x) Loves(x, y)
如果每个人都被某个人爱,则命题为真,但某个人未必是同一个人。例如,如果Kim爱Kim,Terry爱Terry,但是他们彼此不相爱,则,
(y) (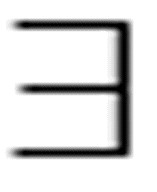 x) Loves(x, y)
x) Loves(x, y)
为真,但是,
(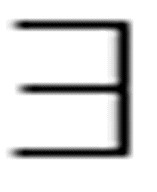 x)(y)Loves(x, y)
x)(y)Loves(x, y)
为假。然而,如果以存在量词开头的命题为真,那么另一个以全称量词开头的命题也为真。你在本章开头看到的《数学原理》中的定理*11.26里就包含了这个关系:
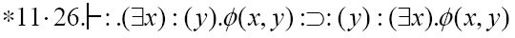
其中ø(x, y)是谓词。图灵采用的记号为:
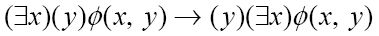
当公式中出现一连串全称量词时,可以任意改变它们的顺序,而不会影响公式的含义。对于存在量词也是如此。(可以把命题转换成复合合取或析取形式来证明这个结论。)然而,一般来说,改变一连串交替出现的全称量词和存在量词的顺序会导致公式含义的变化。
正如命题逻辑中一样,在不考虑域和谓词的含义的情况下,可以计算公式。公式
(x)[F(x) v -F(x)]
是永真的,因为无论域和命题函数F的定义为何,该公式的值永远为真。然而,下面这个公式不可能为真:
(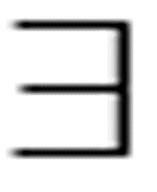 x)(F(x) & -F(x))
x)(F(x) & -F(x))
我们称这样的公式是可驳的。还有其他介于两者之间的公式。下面是个简单的例子:
(x)F(x)
很容易为x想到一个定义域和函数F,使式子为真。例如,假设这个域由自然数组成,F表示“大于或等于零”。定义一个域和函数使得式子为假同样很容易。例如,假设参数是素数时F返回真。这样的公式可以称是可满足的,因为在某些解释下它的值为真。
正确性和可满足性是同一个问题的两个相对面,因为它们的概念是相关的:一个命题或者是可满足的,或者是可驳的。如果一个命题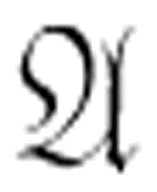 正确,则它是可满足的(但是反之不一定)。如果
正确,则它是可满足的(但是反之不一定)。如果 是可满足的但并不正确,则-
是可满足的但并不正确,则-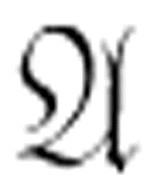 同样也是可满足的但不是可驳的。
同样也是可满足的但不是可驳的。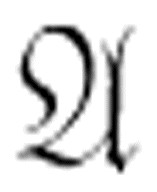 是有效的当且仅当-
是有效的当且仅当-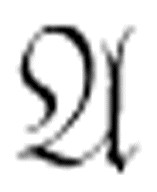 不是可满足的。
不是可满足的。
正确性和可满足性这两个词有时会同数理逻辑的语义方法相结合,之所以这样称呼这些方法,因为它们给出了所涉及命题的真实含义。
数理逻辑的另一种研究方法从本质上说是句法方法。从公理开始推导定理,称这些定理是可证的,因为它们是公理的结果。采用这种句法方法处理逻辑问题,我们就不必牵扯那些麻烦的(可能是形而上学的)“什么是真”的概念。
《希尔伯特和阿克曼》为命题逻辑陈述了四条显而易见的公理,它们出自《数学原理》:
(a) X v X → X
(b) X → X v Y
(c) X v Y → Y v X
(d) (X → Y) → (Z v X → Z v Y)
尽管这些公理仅涉及析取和蕴涵,但如果我们把X & Y定义成 - (-X v -Y)的缩写形式,则还可以把它们应用到合取中。
对于一阶逻辑,《希尔伯特和阿克曼》中为其增加了两条公理。对于任意谓词F,下面的命题都可以看成是公理:
(e) (x)F(x) → F(y)
(f) F(y) → (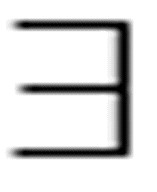 x) F(x)
x) F(x)
除了公理,还有下面这些从原始命题得到复杂命题的规则。
替换:在避免约束变量和自由变量相冲突的情况下,可以用一个公式来替换一个命题变量;如果可以避免冲突,则约束变量和自由变量都可以改变;可以使用公式来代替谓词。
蕴涵:如果公式
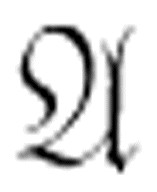 为真,并且公式
为真,并且公式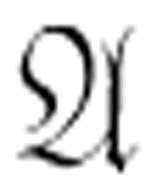 →
→ 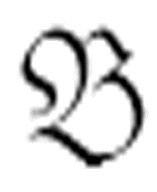 为真,则
为真,则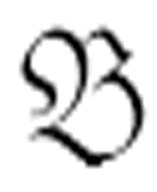 为真。
为真。
第二个规则称为演绎推理(modus ponens),它看上去是显而易见的,但是事实上,它必须是公理。你不能推导出它。如果你非得认为你能做到,那么可以看看刘易斯·卡罗尔的短文《龟对阿基里斯说了什么》。[11]
我们可以把任何从这六条公理和两条规则中推导出来的公式都称作定理。推导过程本身称为证明。证明得出的公式称为是可证明的。一条定理即为一个可证明的公式。
例如,如果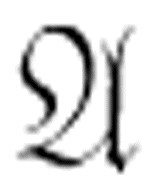 和
和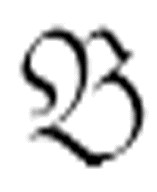 都是定理,则根据公理(c)和规则(1),我们可以说
都是定理,则根据公理(c)和规则(1),我们可以说
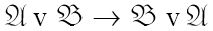
是可证明的,因此它是一个定理。
这些规则的应用方式有两种:从公理开始,然后使用规则推导定理;或者从一个公式开始,使用规则把它转化成一个公理,这种情况下就可以证明这个公式是一个定理。本章开头讨论的自动证明程序就是从《数学原理》的定理出发,然后通过应用公理和替换规则,最后把它们划归为公理的。
可以看到,希尔伯特将数学形式化,就像是把它归纳为符号操作的机械过程。这对亨利·庞加莱(1854—1912)来说是很显然的。庞加莱写道:“想象这样一台机器,我们从一边输入公理,然后从另一边得到定理,就像芝加哥的传奇机器,猪活着进去,出来时就变成火腿和香肠了”。[12]
你甚至可以用系统化的方式机械地列举出所有的定理。从公理出发,可以把它扩展为任意数目的命题变量和谓词,然后在每一种可能的组合情况下应用替换和蕴涵规则。
根据定义,定理就是可以从公理推导出来的公式,因此这种定理的枚举方法可以产生所有可能的定理。这里就出现了一个问题:这些定理和永真的公式相同吗?或者,可能存在不能从公理推导出的永真公式吗?
以《希尔伯特和阿克曼》一书作为出发点,库尔特·哥德尔于1929年在其博士论文《关于逻辑演算的完备性》中,首次建立了一阶逻辑的语法方法和语义方法之间的等价关系,随后在1930年的《逻辑函数演算中公理的完备性》论文中再次提出该关系。
在哥德尔之前,人们已经知道每个可证明的公式也是永真的。这一性质称为可靠性,对逻辑系统来说是很重要的。哥德尔证明的是,每一个永真的公式也是可证明的。这可以作为逻辑系统“完备性”的一个定义,的确,哥德尔论文的题目提到了“完备性”。哥德尔的完备性定理证明公理系统是完备的——《希尔伯特和阿克曼》一书为单纯的谓词逻辑提出的公理系统,对于枚举出该逻辑中的每一个永真命题来说是足够的。
可以设想,定理的枚举和哥德尔的完备性定理为一阶逻辑的判定过程提供了依据。例如,假设你想判定公式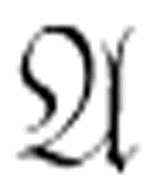 是否是可证明的,可以先列举所有的定理,并且把它们与
是否是可证明的,可以先列举所有的定理,并且把它们与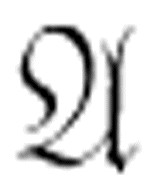 相比较。然而,如果
相比较。然而,如果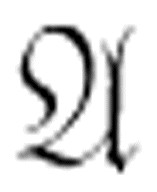 是不可证明的,你就无法得到匹配,也不知道何时该停下来。
是不可证明的,你就无法得到匹配,也不知道何时该停下来。
你一定想到了更聪明的做法:列举所有的定理,然后把每个定理及其否定式和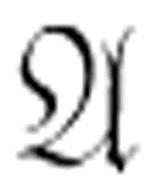 进行比较(或者把每个定理同时与
进行比较(或者把每个定理同时与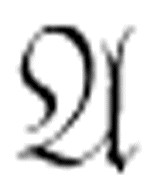 和它的否定式进行比较)。但是,这样做你仍然不能保证可以找到匹配,因为
和它的否定式进行比较)。但是,这样做你仍然不能保证可以找到匹配,因为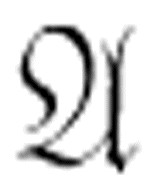 可能仅仅是可满足的,而不是永真的或可驳的。因此,基于枚举的判定过程称为半可判定的。只有当你预先知道
可能仅仅是可满足的,而不是永真的或可驳的。因此,基于枚举的判定过程称为半可判定的。只有当你预先知道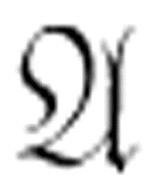 或
或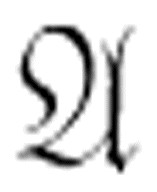 是永真的时候,这类过程才能成功地得到结论。甚至在哥德尔发表了1930年的论文之后,一阶逻辑的判定性问题仍然是个未解决的问题。
是永真的时候,这类过程才能成功地得到结论。甚至在哥德尔发表了1930年的论文之后,一阶逻辑的判定性问题仍然是个未解决的问题。
1931年,哥德尔发表了更著名的论文,涉及一阶逻辑在基本算术中的应用——加和乘。使用这种算术,哥德尔能够把一个数与每个公式和每个证明都联系起来。他还为“可证明”构造了一个名为Bew[13]的谓词,并把这个谓词应用到其否定式的哥德尔数中,得到断定自身不可证明的公式。
因此,在支持基本算术的逻辑系统中,构造出既不是可证明的又不是不可证明的命题是可能的。尽管这一理论后来称为哥德尔不完备性定理,但那篇论文的题目其实是《论“数学原理”及其相关系统的形式不可判定命题I》[14]。标题指的不是完备性或不完备性,而是不可判定命题。
哥德尔的不完备性理论对通用判定过程是毁灭性的打击吗?也不一定,尽管与1930年相比,在1931年,这个通用判定过程确实看上去更加不可能存在了。哥德尔的不完备性定理是关于不可判定命题的,而判定性问题关心的是,是否存在通用过程来判定某个给定公式的可证明性。如果存在通用判定过程,那么它可以把一个不可判定的命题归为不可证明的。
证明《数学原理》中定理的早期计算机程序肯定没有采取这种方法,而是从公理出发,系统地推导出所有可证明的公式。纽厄尔—西蒙—肖的论文将这种方法称为“大英博物馆算法”,如此称呼是因为该方法类似于在大英博物馆中检验每一个物品,希望发现你确实想要的那一件。在这种暴力方法刚一提出时,这些早期的研究学者们就反对它,正如马丁·戴维斯所说的:
显然,从某个逻辑系统的公理出发,在所有可能的方向上尝试系统地应用推导规则来证明某些“非平凡”事物,肯定会带来巨大的组合爆炸。[15]
只有一位编程者不担心组合爆炸,他就是阿兰·图灵。图灵的虚拟计算机拥有无限的存储空间和充裕的时间,因此他可以尝试其他更多担心受机器限制的程序员们所不敢触及的问题。
在前一章中,我在第9节“可计算数的范畴”的中间部分停了下来。图灵在第9节开始就要我们相信通过他的机器进行计算的数包括了“所有被自然当做可以计算的数字”(图灵论文第249页,本书第176页)。
然后,图灵以罗马数字I(表示几个论点中的第一个)和“类型(a)”(直觉的引导)为标题开始了第一小节。下一小节以罗马数字II和“类型(b)”开头,这是图灵的第二个论点。“类型(b)“是指”两种定义等价的证明(新的定义有更多的直觉成分)”。
标题后的一句话有三个脚注。第一个只是阐明他要论述的是受限的谓词演算,也就是我们所说的一阶谓词逻辑。暂时忽略第二个脚注,我们会尽快讨论它。
II. [Type (b)].
If the notation of the Hilbert functional calculus† is modified so as to be systematic, and so as to involve only a finite number of symbols, it becomes possible to construct an automatic‡ machine,, which will find all the provable formulae of the calculus§.
† The expression “the functional calculus” is used throughout to mean the restricted Hilbert functional calculus.
‡ It is most natural to construct first a choice machine (§ 2) to do this. But it is then easy to construct the required automatic machine. We can suppose that the choices are always choices between two possibilities 0 and 1. Each proof will then be determined by a sequence of choices i1, i2, …, in (i1 = 0 or 1, i2 = 0 or 1, …, in = 0 or 1), and hence the number 2n + i12n-1 + i22n-2 + … + in completely determines the proof. The automatic machine carries out successively proof 1, proof 2, proof 3, …
§ The author has found a description of such a machine.
II. [类型(b)]
如果修改希尔伯特的谓词演算†中的记号,使它们系统化并且只涉及有限的符号,那么就有可能构造一台自动‡机器,用来寻找演算过程中所有可证明的公式§。
† “谓词演算”表示受限的希尔伯特谓词演算。
‡ 最自然的事情就是首先构造一台选择机器(§2)来完成这个工作,然后就可以很容易构造想要的自动机器了。我们假设总是在两个可能性0和1之间进行选择。这样,每个证明都由一个选择序列i1, i2,…, in(i1= 0或1, i2=0或1,…, in=0或1)决定,因此,数2n + i12n-1 + i22n-2 + … + in就完全决定了证明。自动机器依次执行证明1、证明2、证明3……
§ 作者发现了对这样一台机器的描述。
我相信,图灵把机器称作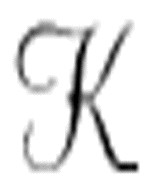 是用来代表德语单词Kalküi。尽管这一点在这句话中不是很明显,但是最后你会发现图灵描述的是一个大英博物馆算法。机器
是用来代表德语单词Kalküi。尽管这一点在这句话中不是很明显,但是最后你会发现图灵描述的是一个大英博物馆算法。机器 可以从已经编码在磁带上的公理开始,也可以一开始就在磁带上写下公理。这些公理包括一阶逻辑中的基本公理以及谓词需要的其他公理。机器逐步地执行推导规则来产生演算中所有可证明的命题。
可以从已经编码在磁带上的公理开始,也可以一开始就在磁带上写下公理。这些公理包括一阶逻辑中的基本公理以及谓词需要的其他公理。机器逐步地执行推导规则来产生演算中所有可证明的命题。
图灵要求修改一阶逻辑的记号来“使它们系统化”。毫无疑问,我们不想困扰于仅仅是变量名称或不必要的括号使用所造成的不同命题间的等价性。例如,下面的三个命题是完全相同的:
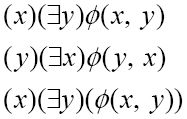
使记号系统化的一个方法是要求变量总是以xi的形式出现,并且它们在某个特定公式中出现时必须遵循下标的数字顺序。另外,括号只有在需要调整运算顺序时才能使用。另一种方法(它与实际机器中采用的方法更类似)是把公式编码成前缀形式,这样就没有必要使用括号,比如卢卡西维茨(1878—1956)专门为命题逻辑发明的所谓的波兰表示法。命题
(A v B) & (C v D)
就可以编码成:
&vABvCD
这里重要的是,这台机器要产生所有可证明的公式。从哥德尔的完备性定理中,我们知道这些所有可证明的公式集合和所有永真的公式集合是相同的。
我相信,图灵在试图吸引那些其论文的早期读者,他们可能对图灵的机器可以计算任意复杂度的实数的能力表示怀疑。1936年,人们对一阶逻辑效力的信任超过了计算机器。从实施的角度看,机器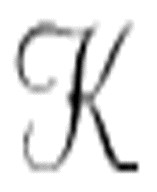 看上去很可行,它确实比计算实数(如10的7次方根)的机器要简单很多。机器
看上去很可行,它确实比计算实数(如10的7次方根)的机器要简单很多。机器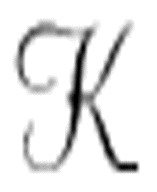 仅采用字符串工作,并根据替换规则以各种方式将这些符号组织在一起。对于很多字符串比较和替换逻辑,图灵在其通用机中所使用的函数里已经有所体现了。
仅采用字符串工作,并根据替换规则以各种方式将这些符号组织在一起。对于很多字符串比较和替换逻辑,图灵在其通用机中所使用的函数里已经有所体现了。
这一句中的第二个脚注——以“最自然的……”开头的脚注,其实看上去是要描述另一种不同的方法,与一阶逻辑相比,这种方法更适合于命题逻辑。给出固定数目的n个命题变量,你可以构造一个系统来产生所有由这些变量和逻辑连接词交替构成的合式公式。对其中的每个公式,都可以使用真值表方法来判断其是否是一个重言式。
如果这个合式公式包含n个命题变量,则需要2n次测试来决定它是否是正确的。如果把真和假分别看作二进制数字0和1,则每次测试都与一个n位的二进制数对应,该二进制数中的每一位都表示一个变量的真值。图灵脚注里的二进制数有点错误,应该去掉开头的2n项。这些试验可以从0开始编码一直到n-1,对应n位二进制数的值。
尽管图灵需要使用这台机器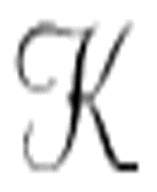 来产生一阶逻辑而不是命题逻辑中的命题,但是我们可以发现,无论何时需要整数,他都只要求一个由非负整数构成的有限的域。他从来不要求一个无限的域,因此不难想象,我们可以把他的一阶公式转换成命题公式,然后就能使用真值表的方法了。
来产生一阶逻辑而不是命题逻辑中的命题,但是我们可以发现,无论何时需要整数,他都只要求一个由非负整数构成的有限的域。他从来不要求一个无限的域,因此不难想象,我们可以把他的一阶公式转换成命题公式,然后就能使用真值表的方法了。
把自然数引入一阶逻辑系统总是有点杂乱,但是如果要把这个逻辑应用到数值概念中,那就非常有必要了。把数字合并进逻辑通常从皮亚诺公理出发。这五个公理来自1889年,朱塞佩·皮亚诺在他的一本小册子《算术原理:一种新的方法》[15]中提出了最初的九条公理,皮亚诺公理就是从这些公理中提取出来的,它的提出也基于了理查德·戴德金1888年出版的一本小册子《什么是数字,什么应该是数字》[16]。
皮亚诺公理是围绕“后继”概念建立的。“后继”就是直觉上一个数后面紧跟的下一个数。例如,12的后继是13。皮亚诺公理保证每一个数都有一个后继,并且该后继是唯一的。在皮亚诺的构造中,只有一个数不是其他任何一个数的后继,这个数是1。不过现在,一般情况下我们定义自然数是从0开始的。
下面是皮亚诺公理的一种通俗易懂的版本:
零是一个数;
每个数都有一个后继,它也是数;
零不是任意数的后继;
后继数相同的两个数是相等的;
任意关于自然数的命题,如果它对零为真,并且它对某个数为真就意味着它对该数的后继也为真,则该命题对所有的数均为真。
第5条公理通常称为数学归纳原理,它是很多涉及自然数的数学证明的基础。(在后两章中,图灵会在证明中两次使用到它。)然而,用一阶逻辑语言表达归纳法是有问题的。归纳法是二阶逻辑固有的概念,因为它必须适用于所有包含自然数参数的谓词。相等也是二阶逻辑的概念,这正是逻辑学家(及图灵在其论文中)不愿意引入在两个参数相等时值为真的谓词的原因。
即使在一阶逻辑语言中表达前四条皮亚诺公理也不是一件容易的事,而且(正如你将看到的)图灵的表示也是不充分的。这个问题对他的证明或结论没有什么实际影响,不过它确实令人不安。
另一个问题涉及自然数本身的表示。传统上使用0, 1, 2, 3,…的奇特表示方法不会产生这个问题。几个世纪的惯例以及小学课程的强行灌输告诉我们,12的后继就是13。特别地,如果我们构思符号操作的机械形式,更好的做法是让符号本身传达“后继关系”的概念。
在《数学基础》(1934)的第一卷中(图灵在论文中引用的一本书),保罗·贝奈斯使用“′”来表示一个数是另一个数的后继。例如,如果a是一个数,则a′表示该数的后继,a″表示下一个后继。贝奈斯还使用符号0来表示零,此时,0′是0的后继,0″是再下一个后继。[17]它究竟是哪个数字呢?只需要数一下0上“′”的个数就可以知道。在希尔伯特及其追随者的著作中,我最早看到这种标注方式的是大卫·希尔伯特1927年发表的《数学基础》。[18]
图灵没有完全使用这种方式。显然,他甚至不太愿意使用符号0,而是使用符号u表示第一个自然数。(他并没有交代u究竟是0还是1,即使这很重要。在我的例子中,我都假设u表示0。)u的后继则为u′ 、u″、u″′等。在表示大数时,这种记号就不太灵活了,并且它不能表示如n或x的任意数。受到《希尔伯特和贝奈斯》的启发,图灵使用u(r)表示u的右上方有r个“′”。例如,u″″′可以表示成u(5),我们知道这就是一只手的手指个数。
图灵定义了一个命题函数N(x),当x为非负整数时,该函数的值为真。如果我们总是把自己限制在非负整数的范围内,那么这个函数对我们没有任何意义,然而,图灵发现可以使用它表示皮亚诺公理。
图灵还定义了一个命题函数F(x, y),当y是x的后继,或者用普通算术描述为y = x + 1时,该函数的值为真。记住,F并没有提供或计算出这个后继。它是程序员们所谓的布尔函数,只有在y确实是x后继的情况下,才为真。
一旦定义了一个好的后继谓词(例如命名为Succ,这样命名仅仅是为了和图灵定义的谓词区分开来),并且为数学归纳法的使用建立了一个公理,那么就可以定义一个名为Sum(x, y, z)的谓词,当z的值与x + y的值相等时,这个谓词的值为真。这个谓词Sum基于以下三条公理:
(x)Sum(x, u, x)
(x)Sum(u, x, x)
(x)(y)(z)(r)(s)(Sum(x, y, z)&Succ(y, r)&Succ(z, s)→Sum(x, r, s))
前两条公理定义了零和任意一个数的加法运算。第三条的含义是:如果x + y = z,r = y + 1,s = z + 1,那么x + r = s。
类似地,可以定义谓词Product(x, y, z)如下:
(x) Product (x, u, u)
(x) Product (u, x, u)
(x)(y)(z)(r)(s)( Product (x, y, z) & Succ(y, r) & Sum(z, x, s) → Product (x, r, s))
前两条公理定义与零的乘法运算,第三条的含义是:如果x × y = z,r = y + 1,z + x = s,那么x × r = s。
我们再做进一步的分析。定义如下的谓词IsEven(x):
(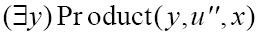
如果存在这样的y满足x = y × 2,那么IsEven(x)为真。IsOdd(x)与-IsEven(x)相同。我们已经有了足够多的谓词,因此这里不再继续定义了。
Now let α be a sequence, and let us denote by Gα(x) the proposition “The x-th figure of α is 1”, so that— Gα(x) means “The x-th figure of α is 0”.
The negation sign is written before an expression and not over it.
令α是一个序列,我们用Gα(x)表示命题“α的第x个数字是1”,于是,-Gα(x)表示“α的第x个数字是0”。
否定符号写在表达式的前面,而不是上面。
上面的脚注表明,图灵采用的否定记号和希尔伯特的不同。α是一个序列,这个序列可以通过设计一个专用机器按常规计算得到。这里,图灵建议我们根据数字1或0来对应建立值为真或假的谓词。例如,第6节中得到的对应于2的平方根的序列以
1011011010…
开头。
如果从0开始对每一位上的数进行编号,那么Gα(0)的值为真,Gα(1)的值为假,Gα(2)的值为真,Gα(3)的值为真,Gα(4)的值为假,等等。这个谓词好像很复杂。图灵例I中机器对应的序列要简单得多:
0101010101…
你可以回想起这个序列正是1/3的二进制等价形式。如果将Gα(x)定义为IsOdd(x),则描述这个序列的命题函数是很简单的。
Suppose further that we can find a set of properties which define the sequence α and which can be expressed in terms of Gα(x) and of the propositional functions N(x) meaning “x is a non-negative integer” and F(x, y) meaning “y = x + 1”.
进一步假设我们可以找到一组性质来定义序列α,并且可以用Gα(x)和命题函数N(x)、F(x, y)来表达这些性质,其中,N(x)表示“x是一个非负整数”,F(x, y)表示y = x + 1。
图灵在这里引入的两个谓词将在论文的剩余部分中经常用到。F是一个后继函数,它对于自然数的定义很重要。如果定义域明确限制为自然数,我认为不需要定义函数N。
我不确定图灵所说的“一组性质”指的是什么。我们这里需要的是能为构成Gα(x)的命题函数提供支持的公理。在我给出的简单例子中,这些公理包括支持谓词Sum和Product的公理。
When we join all these formulae together conjunctively, we shall have a formula,say, which defines α.
用合取符号把这些公式连接起来,我们可以得到一个定义α的公式,将其命名为。
公理的合取式不一定真正地定义了α,因为它无法为定义α提供基础。
The terms ofmust include the necessary parts of the Peano axioms, viz.,
(u) N(u) & (x) (N(x) → (
y) F(x, y)) & (F(x, y) → N(y)),
which we will abbreviate to P.
的项中必须包含皮亚诺公理的必要条件,也就是:
(u)N(u)&(x)(N(x)→(
y)F(x,y))&(F(x,y)→N(y))
后文中我们将其简写作P。
当然,P指的是皮亚诺,它是三个项的合取式。第一项表示u存在,第二项的含义是对每一个x都存在一个y是它的后继,第三项指的是一个数的后继也是一个自然数。这个公式不能说明零和后继的唯一性,这是个问题。《希尔伯特和贝奈斯》中为后继函数(他们称之为S[19])给出了以下三个公理:
(x)(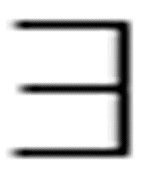 y)S(x, y)
y)S(x, y)
(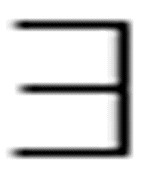 x)(y) - S(y, x)
x)(y) - S(y, x)
(x)(y)(r)(s)(S(x, r) & S(y, r) & S(s, x) → S(s, y)
第一条公理声明每个数都有一个后继;第二条的含义是存在一个没有后继的数;第三条是说,如果r是x和y的后继,x是s的后继,那么y也是s的后继。第三条公理实质上确立了后继的唯一性。
When we say “defines α”, we mean that —
is not a provable formula, and also that, for each n, one of the following formulae (An) or
(Bn) is provable.
(An)¶
where F(n) stands for F(u, u′) & F(u′, u″) & … F(u(n-1), u(n)).
¶ A sequence of r primes is denoted by (r).
当我们说“定义了α”时,意思是-
不是一个可证明的公式,并且对每一个n,下面公式(An)或(Bn)中的一个是可证明的。
(An)¶
其中F(n)代表F(u,u′)&F(u′,u″)&…F(u(n-1),u(n))。
¶ 包含r个“′ ”的序列记为(r)。
公式(An)上的脚注是指,按照惯例采用括号中含数作为上标,来表示包含相应数目的“′”。图灵在其后继函数F中也使用上标来表示后继函数的合取,后继函数实际上是说,1是0的后继,2是1的后继,等等。
图灵采用的后继函数的合取是不充分的,因为它不能保证这些后继的唯一性。例如,F(u′, u″′ )的真值是多少?我们无法得知它是假的。一种简单的修正方式是通过包含所有不为真的后继谓词的否定式,如-F(u′, u″)和-F(u′, u),并在u(n)处停止来扩展F(n)(尽管仍是有限的)。
这里的n指的是位数,它从0开始逐个变大。从0位,1位,2位,……逐位生成序列。每一位的计算都只需要有限数目的非负整数,因此公式F(n)是有限个项的合取。然而,在某些情况下,公式可能需要更多的整数。例如,对于第0位,公式只需要u。但是在我的例子中,函数IsOdd的定义还需要u″,因此事实上,F的上标应该是2和n中较大的那个数。
进行这个小小的修正后,下面的公式都将是可证明的:
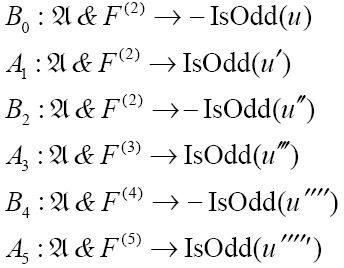
依次类推。回想一下,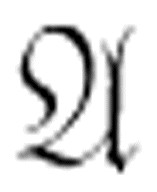 包括支持IsOdd函数所需要的所有公理。这些结果对应了序列的前六位:0,1,0,1,0,1。注意,数字1对应可证明的An,0对应Bn的可证明性。
包括支持IsOdd函数所需要的所有公理。这些结果对应了序列的前六位:0,1,0,1,0,1。注意,数字1对应可证明的An,0对应Bn的可证明性。
[253]
I say that α is then a computable sequence: a machineα to compute α can be obtained by a fairly simple modification of
.
我认为此时的α是一个可计算序列:稍微修改,便得到一个可以计算α的机器
α。
大家会想起,机器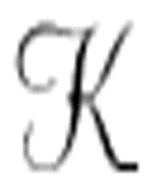 可以从公理推导产生所有的可证明的公式。
可以从公理推导产生所有的可证明的公式。
We divide the motion ofα into sections. The n-th section is devoted to finding the n-th figure of α. After the (n - 1)-th section is finished a double colon :: is printed after all the symbols, and the succeeding work is done wholly on the squares to the right of this double colon. The first step is to write the letter “A” followed by the formula (An) and then “B” followed by (Bn).
我们把α的操作分成几个部分。第n个部分用来寻找序列α的第n位数字。第(n-1)个部分完成以后,在所有符号的末尾打印一个双冒号::,后续的工作全都在这个双冒号右边的格中进行。第一步是写入字母“A”,后面跟着写公式An;然后写入“B”,再紧跟着写Bn。
在这个例子中,n的值为5,机器首先写“A”和“B”,紧跟着分别写入两种可能的情况,如下:
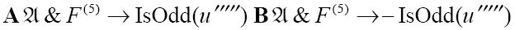
不过,上面的写法也不完全正确:字母“A”和“B”不应该为粗体,项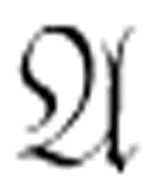 应该是所有公理的显式合取式,F(5)是更多个公理的显式合取式,IsOdd可能是之前定义的Product函数的否定式,所有函数的名字可能变得更加神秘了。
应该是所有公理的显式合取式,F(5)是更多个公理的显式合取式,IsOdd可能是之前定义的Product函数的否定式,所有函数的名字可能变得更加神秘了。
然而,真正的意义在于,这两个命题中的其中一个是可证明的。在这两个打印的公式右边的全部有一整条纸带可以供机器工作。很可能是机器首先把这些公理写在纸带上,然后开始推导可证明的公式。
The machineα then starts to do the work of
, but whenever a provable formula is found, this formula is compared with (An) and with (Bn). If it is the same formula as (An), then the figure “1” is printed, and the n-th section is finished. If it is (Bn), then “0” is printed and the section is finished. If it is different from both, then the work of
is continued from the point at which it had been abandoned. Sooner or later one of the formulae (An) or (Bn) is reached; this follows from our hypotheses about α and
, and the known nature of
. Hence the n-th section will eventually be finished.
α is circle-free; α is computable.
随后,机器α开始从事
的工作,但是无论何时找到一个可证明的公式,这个公式都会与An和Bn进行比较。如果它和An相同,就打印数字1,这样第n个部分就完成了。如果它和Bn相同,则打印0,这个部分也就结束了。如果它和An、Bn都不相同,那么
就从它停止的点继续工作,迟早会遇到An或Bn中的一个。这可以从我们对α和
所作的假设,以及
的性质中推断得到。因此,第n个部分最终会结束。
α是非循环的,α是可计算的。
可以想象,机器 α可以一般化为与图灵的通用机极其类似的机器。它可以以一条已经编码了公理的纸带开始工作,仅仅通过在纸带上写入一些不同的公理和一个不同的函数,机器就能计算通过一阶逻辑定义的任意序列。
α可以一般化为与图灵的通用机极其类似的机器。它可以以一条已经编码了公理的纸带开始工作,仅仅通过在纸带上写入一些不同的公理和一个不同的函数,机器就能计算通过一阶逻辑定义的任意序列。
It can also be shown that the numbers α definable in this way by the use of axioms include all the computable numbers. This is done by describing computing machines in terms of the function calculus.
还可以证明,通过这种使用公理的方式得到的可定义的数字α包含了所有的可计算数,借助函数演算描述计算机器就可以做到。
事实上,在图灵论文的最后一节,即本书的下一章中,图灵将采用一阶逻辑描述计算机器。现在,他想提醒读者,不是每一个数字都可以通过机器计算得到,特别是那些以0和1构成的序列,它们可以告诉我们哪些是符合要求的机器的描述数。
It must be remembered that we have attached rather a special meaning to the phrase “defines α”. The computable numbers do not include all (in the ordinary sense) definable numbers. Let δ be a sequence whose n-th figure is 1 or 0 according as n is or is not satisfactory. It is an immediate consequence of the theorem of § 8 that δ is not computable. It is (so far as we know at present) possible that any assigned number of figures of δ can be calculated, but not by a uniform process. When sufficiently many figures of δ have been calculated, an essentially new method is necessary in order to obtain more figures.
必须牢记,我们为“定义α”这句话赋予了一个特别的含义。可计算数不包括所有(一般意义上)的可定义数。假设δ是一个序列,根据n是否可接受,它的第n位数字可以为1或0。由§8中的定理可以直接得到δ是不可计算的。(就我们现在所知)给定数目的δ中的数字是可计算的,但是无法采用统一的过程。一旦已经计算了足够多的δ的数字后,有必要采用一个本质上更新颖的方法来得到更多的数字。
至此,图灵完成了他的第二个论证,来证明他的机器可以计算通常所谓的可计算数。接下来将要讲述的是他的第三个论证。你或许能回忆起图灵对于一台人类计算者的“思维状态”的依赖。一些读者可能认为,人类“思维状态”是太过虚幻的概念而不能封装在一台机器中。
图灵简单地描述了如何将思维状态这一概念构造成为机器结构的一部分,我们将以此结束本章。
III. This may be regarded as a modification of I or as a corollary of II.
We suppose, as in I, that the computation is carried out on a tape; but we avoid introducing the “state of mind” by considering a more physical and definite counterpart of it. It is always possible for the computer to break off from his work, to go away and forget all about it, and later to come back and go on with it. If he does this he must leave a note of instructions (written in some standard form) explaining how the work is to be continued. This note is the counterpart of the “state of mind”. We will suppose that the computer works in such a desultory manner that he never does more than one step at a sitting. The note of instructions must enable him to carry out one step and write the next note. Thus the state of progress of the computation at any stage is completely determined by the note of
[254]
instructions and the symbols on the tape. That is, the state of the system may be described by a single expression (sequence of symbols), consisting of the symbols on the tape followed by Δ (which we suppose not to appear elsewhere) and then by the note of instructions. This expression may be called the “state formula”. We know that the state formula at any given stage is determined by the state formula before the last step was made, and we assume that the relation of these two formulae is expressible in the functional calculus. In other words, we assume that there is an axiomwhich expresses the rules governing the behaviour of the computer, in terms of the relation of the state formula at any stage to the state formula at the preceding stage. If this is so, we can construct a machine to write down the successive state formulae, and hence to compute the required number.
III. 这一部分可以看成是对I的修正或II的推论。
与I中类似,我们假设计算在一个纸带上进行,但是通过考虑更加机械而确定的类似过程,我们可以避免引入“思维状态”这一概念。计算机总是能在某个时刻暂停,转向其他的操作,然后过一段时间后还可以再返回到之前停止的点继续运行。如果机器这样运行,那么它必须记录一些指令(以某种标准形式写入纸带),以便阐明如何继续当前已经停止的工作。这个记录即与“思维状态”类似。我们假设计算机将以这种不连贯的方式运行,它每次不能执行超过一个步骤。记录的指令必须使得计算机可以执行一个步骤,并且写入下一条记录。因此,计算过程中任意阶段的状态都是由记录的指令和纸带上的符号完全决定的。也就是说,可以采用单一的表达式(符号序列)来描述系统的状态,这个表达式是由符号、之后的Δ(假设Δ不会在其他地方出现)和指令记录组成的,可以称这个表达式为“状态公式”。我们知道,每个给定阶段的状态公式都是由上一个步骤进行之前的状态公式决定的,我们假定这两个公式之间的关系可以采用函项演算来表示。换句话说,假定存在一个公理,它给出了任意阶段的状态公式和前一阶段的状态公式之间的关系,从而管理计算机的行为。如果真是这样,我们可以构造一台机器记下连续的状态公式来计算得到所需的数。