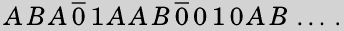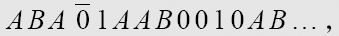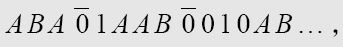第10章

计算机与可计算性

想像一台计算机器，它几乎什么也做不了，图灵事实上是构想了一种用于“通用目的”的多功能计算机，这是一个革命性的观念。在当时，计算机被普遍认为是为某些特定工作特殊设计的。早期类似于计算机的设备，如微分分析仪（由麻省理工学院的万尼瓦尔·布什及其学生设计并构建），就是这一设计方式的例证。微分分析仪具有重要的功能——求解常微分方程，但它所能做的也仅限于此。

即使是那些深入探索构建数字计算机的人们，也很难抓住数字逻辑的普遍规律。如霍华德·艾肯，他从1937年就开始研究数字计算机，是计算机行业一位真正的先驱。然而在1956年，他说道：

如果事实证明，一台用来求微分方程数值解的机器的基础逻辑，与一台为百货店制作账单的机器的逻辑相同，那么这将是我遇到的最令人惊讶的巧合。^［1］

作为一个将计算机视为逻辑机器的人，图灵显然知道的更清楚。当大部分早期的计算机制造者在考虑硬件问题的时候，图灵从1936年起就开始编写软件了。对于图灵来说，即使是加法这样的基本算术运算也可以通过软件来实现。与艾肯在1956年的言论不同，图灵在1950年这样说道：

数字计算机的特殊性在于它们能够模拟任何离散状态的机器。为描述这一点，我们称之为通用机。有了具备这一特性的机器，我们就能得到一个重要的结果：如果不考虑速度，那么就不需要对不同的计算过程设计不同的机器。通过对每个事件恰当编程，所有的工作可以在一台机器上完成。在这种意义下，所有的数字计算机都是等价的。^［2］

图灵引入了一个重要的限制“如果不考虑速度”。有些人也许会说，对于计算机而言，速度不是全部，却不可或缺。当人们需要某种特殊的计算机时，例如为数百万的好莱坞大片做电脑成像，速度通常是主要的考虑因素，而强大的存储能力反而不重要。然而，在实际的数字运算能力上，所有的数字计算机都是通用的。

在关于计算的发展史上，阿兰·图灵的地位从来都不十分明确。在一部权威发展史著作^［3］中，图灵的贡献几乎没有提到；而在另一位著名数学家写的历史中，计算机被看成是数学概念的物理体现^［4］，图灵就被视为一个最重要的人物。图灵在计算历史著作中的地位取决于到底是从工程和商业的角度，还是从数学和学术的角度来看待计算机。

图灵一个令人感兴趣的角色涉及图灵和约翰·冯·诺依曼的关系。他们的第一次见面是在1935年4月，当时冯·诺依曼从普林斯顿大学来到剑桥大学讲授关于殆周期函数的课程。在此之后，图灵决定加入普林斯顿大学。^［5］ 1936年秋，图灵到达普林斯顿大学后，他们又取得了联系。^［6］冯·诺依曼一度声称，在哥德尔的不完备性定理之后便不再读数理逻辑方面的论文了，^［7］所以我们并不知道他到底什么时候读了“可计算数”那篇论文。这两位数学家也有其他共同的数学兴趣（殆周期函数和群论），这些是冯·诺依曼在1937年6月1日为图灵写的关于普罗科特奖学金的推荐信中提及的。

1938年7月，图灵离开普林斯顿之前，冯·诺依曼为他提供了一份年薪1500美元的工作，是在高级研究院担任自己的助手，但是图灵没有接受。当时，冯·诺依曼必然已经读过了图灵的论文。在图灵传记中，安德鲁·霍奇斯向物理学家斯坦尼斯罗·乌拉姆（当时也在高级研究院）询问冯·诺依曼对图灵的评价（冯·诺依曼逝于1957年，时年53岁）。乌拉姆回忆起1938年夏天同冯·诺依曼一起旅行时，当时冯·诺依曼建议玩一个游戏。

在一张纸上写下一个尽可能大的数，用一种与图灵模式有关的方法来定义它…冯·诺依曼对他十分赏识，早在1939年就和我提到他的名字，并且说这是一个“聪明的主意”……1939年，冯·诺依曼在考虑用机械方法来研究形式化数学系统时，曾数次向我提到图灵的名字。^［8］

早年和图灵之间的这些接触，在1944年9月冯·诺依曼到达宾夕法尼亚大学的穆尔电气工程学院时突然变得非常重要。当时正在建造的计算机叫作ENIAC（电子数字积分计算机）。这个由约翰·埃克特（1919—1995年）和约翰·威廉·莫奇利（1907—1980）设计的30吨的庞然大物，虽然建造出来了，但是它的局限性越来越明显。于是一个叫EDVAC（电子离散变量自动计算机）的替代品列入了后续计划之中。

从一开始，冯·诺依曼就不单单从潜在用户，也从科学家和技术人员的角度来考虑问题。在1944年剩下的时间以及整个1945年，他并不在洛斯阿拉莫斯国家实验室，他参加了EDVAC方面的技术会议，做出了很多技术贡献，并且在逻辑设计方面提出了很多建议。^［9］

然而，1945年6月30日，当一篇以约翰·冯·诺依曼为唯一作者的“EDVAC的第一份草案报告”^［10］ 出现时，争议的火焰被点燃了，即使在今天仍然余烟未尽。这篇报告强调了一些概念，比如计算机应该是电子的，必须使用二进制数，以及程序应该存储在内存中。但是也许再也无法完全确定，这些概念是冯·诺依曼自己提出的，还是他只不过是将在穆尔学院构建ENIAC时的想法组合了一下。数十年来，当人们描述数字计算机的时候总是会提到“冯·诺依曼体系结构”，现在这个词渐渐地不再使用，很大程度是因为这样称呼缺乏对在计算机体系结构上有所贡献的其他人的尊重。

“EDVAC的第一份草案报告”只引用了一篇出版文献，它是发表在期刊《数学生物物理学公报》上题为“神经活动内在概念的逻辑演算”^［11］的论文。这篇引用文献表明了冯·诺依曼在计算机和人脑关系上的兴趣，同样有趣的是，这篇论文的作者所提出的大脑的生理学概念正是基于图灵机的方法。麦卡洛克和匹茨的论文同样被诺伯特·维纳（1894—1964）的经典著作《控制论：关于在动物和机器中控制和通信的科学》（1948）所引用。我会在第17章详细讨论麦卡洛克、匹茨、维纳和冯·诺依曼。

物理学家斯坦利·弗兰克尔曾在洛斯阿拉莫斯与冯·诺依曼一起工作，他还记得冯·诺依曼对于图灵1943年（或1944年）发表的那篇论文是如此地充满兴趣：

冯·诺依曼向我介绍了那篇论文，在他的催促下我认真地阅读了论文。很多人都称冯·诺依曼是“计算机之父”（以现在对这个词的理解），但是我保证他自己从未犯过这样的错误。他一直和我（肯定还有别人）强调，这些基础概念都是属于图灵的（图灵达到了巴贝奇、埃达和其他人都预想不到的高度），而他只是起了助推的作用。在我看来，冯·诺依曼的本质角色就是，让世界知道图灵的这些基础概念，并在穆尔学院和其他地方进行了研究工作。^［12］

20世纪40年代末，冯·诺依曼似乎已经向一些人提到图灵工作的重要性。例如，1946年，他在给诺伯特·维纳的信中写道：“图灵的一个伟大贡献……，明确了一种机制可以是‘普遍的’。”^［13］

虽然阿兰·图灵多数情况下是因为他的论文而被人们铭记的，但是他的名字同样与三个大型计算机项目相联系。

第一个项目是巨人（Colossus），1943年制造于布莱切利庄园的破译密码的计算机。它是由托马斯·弗劳尔斯（1905—1998）设计的，20世纪30年代他在英国邮政电话分部的研究实验室工作，熟悉开关电路和电子学。虽然一些人认为图灵也参加了巨人项目^［14］，但是很显然，他并没有。他当然知道这个项目，但是“拒绝受邀负责其中一个主要部分”^［15］。尽管如此，图灵论文对巨人的逻辑设计的影响是公认的。^［16］

图灵更多参与的是位于伦敦西南部特丁顿的国家物理实验室（NPL）的计算机项目。1944年，NPL的领导者是查尔斯·达尔文爵士（1887—1962）^［17］，他的祖父曾撰写了在生物学上颇具影响的著作。达尔文创建了一个“数学部”，其工作就是研制自动计算机器。

数学部的负责人J. R. 沃默斯利在1945年6月招图灵来NPL面试。^［18］沃默斯利读过那篇“可计算数”，并且希望图灵设计一台“自动计算引擎”（ACE）的计算机，而“引擎”这个词有意无意中唤起了他对查尔斯·巴贝奇的回忆。

图灵那时已经读过了冯·诺依曼那篇关于EDVAC的报告，对他自己的计算机有了一些想法，并在1945年结束之前完成了报告“在数学部中开发自动计算引擎的方案”。图灵的报告虽然说“对提出的计算器有了十分全面的考虑”，但还是建议“与冯·诺依曼‘关于EDVAC的报告’一起阅读”。^［19］

图灵提出的机器是电子的，使用二进制数字（虽然位和位需要连续传输），具有1MHz的时钟速率。它使用水银延迟线存储器，通过水银管中的声波脉冲来存储比特信息。一个五英尺长的水银管可以存储1024比特的数据。每一比特从水银管的一端传送到另一端大约需要1毫秒，这样它可以被存取并返回水银管的开始再利用。图灵预计，一个32比特的数的加法需要32微秒（每一比特一微秒），而32比特的数的乘法需要“超过2毫秒”的时间。^［20］

图灵的设计只用了很少的原始指令，大部分可以在寄存器和内存之间传输。这种情况下，它类似现代的精简指令集计算机（RISC）——采用较快的硬件，更复杂的工作由软件完成。图灵似乎还发明了栈——最终成为了计算机存储的常用类型，类似于自助餐厅里用弹簧托架摞得很高的一堆盘子。最后一个盘子“推”进栈里，成为下一个要被“弹”出的盘子。图灵将这两个方法分别叫“盖住”（BURY）和“掀开”（UNBURY）。^［21］

图灵在1947年2月20日给伦敦数学协会写的讲稿中，对计算给出了更具个人观点的说法：“类似ACE这样的计算机器……实际上是更加实际的通用机器。”这个机器必须做的工作的复杂性就是“要专注于纸带”（其实就是软件），“而且不应该以任何方式出现在通用机器中”。^［22］ 图灵认识到了计算机速度的重要性，当然，他还强调了大存储的好处：

我相信提供适当的存储器是解决数字计算机问题的关键。如果想让计算机可以拥有人工智能这一说法更具有说服力，必须提供比现在多得多的存储能力。在我看来，制造大的内存要比用更快的速度计算诸如乘法的运算重要得多。^［23］

正如所料，图灵清楚地认识到了二进制相比于十进制而言所拥有的优势：

对于大规模计算机而言，使用二进制是很自然的事情。在二进制范围内，计算更简单，因为制定只有两个固定位置的机制很容易。^［24］

在讲稿的最后，图灵特别提到了可以修改自己指令集的机器：

就像一个小学生，他从老师那里学到了很多东西，同时通过自己的学习也增长了很多知识。我觉得，当理应把这台机器看作是在展示智能的时候，就会是这种情况。^［25］

到了1947年9月，ACE缺乏进展开始令图灵感到沮丧。他请了一年的半薪休假，离开了剑桥。NPL期望图灵至少能再回来工作两年，但是他没有回来。（实验版的ACE一直到1950年才就绪，而且已经和图灵当初的设计偏离了许多。）

而图灵加入了从1945年就在曼彻斯特大学的麦克斯·纽曼的队伍里。纽曼获得批准，建立了一个新的计算机器实验室，并制造了一台叫做Mark I的机器。在1948年6月，Mark I成为了“第一台完工的EDVAC类型的电子程序存储计算机”。^［26］

图灵在9月加入了曼彻斯特大学的数学系，参与纽曼的新项目。两个月后，他们和曼彻斯特的一个电子制造商费伦蒂有限公司达成协议，为后者制造商业化的机器。

图灵基本上是负责Mark I的编程工作。大约1951年，图灵接受的任务是为这个机器产品编写第一本“程序员手册”。在手册中，图灵将编程定义为：“一种使数字计算机按照人的意愿工作，并将其正确表达在穿孔纸带上的活动。”^［27］

除了使用水银延迟线，Mark I还使用了阴极射线管（CRT）来做存储器。这种存储器一般称为威廉姆斯管，是1946年12月来到曼彻斯特的F. C. 威廉姆斯率先研究出来的。需要存储的数据以电脉冲形式发送到CRT，然后用一组点阵显示在屏幕上，每个点代表一个比特。用不同密度或大小的点来区分0和1。电子管前的金属盘用来接收这些点，并且允许电子管进行刷新或者读取。另一个CRT允许人们来查看这些点并且检查数据。到了1947年，每个CRT都可以存储2048比特的数据。

Mark I用40比特的字来存储数据，这样可以存储两条20比特的指令。这些字以5比特一组显示在CRT上，其中每个5比特码由对应这个码的电传打印机字符表示，由此开发了一种32进制的记法。为了读一个数字，需要知道每个字符对应的码。这些字符码并不是以字母顺序排列的，按照图灵的做法，每个想要在Mark I上开发程序的人都需要记住这个32字符的序列：

图灵参加这些实际的计算机项目可能会让我们忽略一个简单的事实：图灵“可计算数”论文的目的并不是设计一个通用的计算机器。这篇论文的全部目的是希望用这个假定的计算机来帮助解决判定性问题。这里还有几个步骤要做。一个关键的步骤就是要证明，图灵机本质上会被限定在它能做的事情中。

图灵在论文的引言中提到：“尽管可计算数如此之多，并且在很多方面与实数相似，但它是可数的。”（论文第230页，本书第57页。）在第5节中，他证明了“每个可计算序列至少对应一个描述数，但不存在一个描述数对应多个可计算序列。因此，可计算序列和可计算数是可数的。”（论文第241页，本书第125页。）

仍有一些疑问。很显然，可计算数很多，至少包含一些超越数。用图灵机计算π、e或者刘维尔常数是完全可能的。确实，数位之间符合某种次序的超越数是图灵机可计算的，这就是乌拉姆和冯·诺依曼在一起旅行时玩的游戏。

然而，大部分……不不不，我们现实点，就说“事实上全部”吧。事实上，全部的超越数都貌似其数位是随机的。在实数领域，数位序列的顺序性或者可计算性并不怎么提及，常提到的是完全性和总体随机性。

你如何制造一台可以计算一个没有规律的数的机器呢？你只是随机地生成数位吗？

随机性不是计算机能处理好的事情，但是计算机经常要求一些随机的行为。一些统计程序需要随机数，一些电脑游戏需要随机数来改变行为。没有随机数，纸牌游戏的每手牌都会完全一样。

程序语言总是为程序员提供一些标准方法来生成随机数。例如，用C语言写的计算机程序可以使用叫做rand的函数来获得一个0到32767之间的随机数。rand函数从一个叫做种子的数开始，种子初始化默认为1。不同的rand函数可能以不同的方式来实现算法。例如，下面是rand函数的微软C语言^［28］实现：

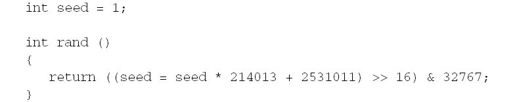
这个rand函数将种子乘以214 013，然后加上2 531 011，再后用这个结果替换种子，供rand函数下次调用。然而，种子被定义为32位有符号整数，可能会出现向上溢出或者向下溢出。计算的结果会截位至32位，如果最高位是1，那么结果实际上是负的。^［29］计算过程接着将结果移动16位，相当于将它除以65 536，然后截掉多出来的。最后在结果和32 767的位之间进行AND布尔运算。这样会去掉除低15位外的所有位，确保结果在0到32 767之间的。

即使你不理解上述费解的计算，也能看出rand函数其实不会真的生成随机数！这个函数是完全确定的。从种子值为1开始，重复地调用函数总是产生一系列相同的计算结果：

41

18 467

6 334

26 500

19 169

…

程序第一次调用rand，函数会返回41，而第30 546次调用rand，函数还是会返回41，然后一直重复。

这样的结果序列完全取决于种子和算法，它并不是真正随机的，它被称为伪随机序列。如果在rand函数生成的数字上进行统计实验，它们会表现出随机性。在一些应用程序中，伪随机序列可能比真正的随机数更好，因为它可以重新产生结果来测试程序是否正常运行。

然而，在游戏中并不希望看到总是产生相同的一串随机数。鉴于此，每次处理纸牌游戏中的一手新牌时，程序可能会获得当前的时间，并精确到秒和毫秒，然后用此来设定新的种子。假设你不会在一天里的同一个时间（精确到毫秒）同时处理两手牌，那么你得到的牌看起来就是随机的。

约翰·冯·诺依曼曾经说：“任何想用算术方法来产生随机数的人都是有罪过的。”^［30］（这在他描述了用算术方法来产生随机数之前是正确的。）因为计算机是没有能力产生随机数的，如果应用程序真的需要一个随机数，那么就必须抛开计算机用特定的硬件来做这件事。硬件随机数产生器（RNG）可以使用环境噪声或者量子过程来产生随机数。

令人好奇的是，阿兰·图灵似乎想到了在硬件上生成随机数的方法。图灵提出，在曼彻斯特大学研制的Mark I的生产模型中要有一条特别的指令：从噪声源生产随机数。结果，随机数并没有预想的那么随机，不过已经足够让你不必像通常那样去调试它了。^［31］

我们假设有一个硬件RNG，用它来产生一个0和1的序列，就像图灵机那样。在序列前放一个二进制小数点，你会看到一个实数（毫无疑问是超越数）在你面前被正确构造了出来。（如果你使用软件来生成伪随机序列，种子最终会被重新计算，序列会重新开始。得到的数字会由一些重复的数位序列组成，这意味着它是一个有理数。）

现在定义一个图灵机，它生成的实数与硬件RNG生成的实数完全相同。但是你做不到。复制RNG的唯一方法是图灵机显式地打印每个你想要的数位，但这不是一个拥有有限个格局的图灵机。

也许大多数实数的随机性只是一个幻想。毕竟，π的数位看起来是随机的，但π肯定是可计算的。也许表现出随机性的实数确实有一些我们不知道的底层结构。我们换一个思路考虑这个问题，也许可以证明可计算数是不可数的。然后，我们可以睡个好觉，因为知道了每个实数都是可计算的，我们很欣慰。

图灵需要直面这些挑战。

8. Application of the diagonal process.

It may be thought that arguments which prove that the real numbers are not enumerable would also prove that the computable numbers and sequences cannot be enumerable^*. It might, for instance, be thought that the limit of a sequence of computable numbers must be computable.

^* Cf. Hobson, Theory of functions of a real variable (2nd ed., 1921), 87, 88.

8. 对角线法的应用

人们可能认为，证明实数是不可数的论据同样可以用于证明可计算数及可计算序列是不可数的^*。例如，可以认为一个可计算数序列的极限一定是可计算的。

^* Cf. Hobson， Theory of functions of a real variable（2nd ed.，1921），87，88。

图灵暗指了格奥尔格·康托尔的第一个关于实数是不可数的证明（1874年），我在本书第20页描述过这个证明。似乎图灵当时并未读过康托尔最初的著作，于是他参考了一本由剑桥大学出版社出版^［32］的E. W. 霍布森的书。霍布森的表述与康托尔的十分相似，甚至使用的记号都大部分相同。

图灵认为，使用一系列可计算数而非实数，康托尔的工作是可以重复的。在这两种情况下，数都趋于一个极限。在康托尔的证明中，该极限必然是一个实数（还有其他可能吗？），但是康托尔证明了该极限不在可数的实数集中，并由此证明了实数是不可数的。

当同样的方法用于可计算数时，可计算数列同样趋于一个极限，这个极限仍然是可计算数吗？图灵回答道：

This is clearly only true if the sequence of computable numbers is defined by some rule.

显然，只对在某种规则下定义的可计算数序列成立。

图灵所指的序列是趋于极限的阿尔法或贝塔序列。仅当我们可以对其进行计算时，该序列的极限是一个可计算数，即我们设计一个算法来得到这些阿尔法和贝塔序列接近的数值极限。这看起来不太可能。如果我们没有办法计算这个极限，那么它便不是一个可计算数，只是另一个不可计算的实数，于是我们便无法证明可计算数是可数的。

Or we might apply the diagonal process.

或者我们可以尝试对角线法。

图灵把余下的段落用引号括了起来，看起来像是一位反对者试图在他的论文里说服读者可计算数是不可数的。比起我在第23页提及的，图灵的这个反对者试图找寻一种充斥着大量记号的对角线法来解决问题。

“If the computable sequences are enumerable let α_n be the n-th computable sequence, and let ø_n(m) be the m-th figure in α_n.

“假设可计算序列是可数的，令α_n为第n个可计算序列，ø_n(m)为α_n中的第m个数。

这些只是记号。每一个可计算序列都是0和1的组合，而且这样的二进制位的每一个都可以用希腊字母ø表示。可计算序列可用下标表示成

Let β be the sequence with 1 - ø_n(n) as its n-th figure.

令β是以1-ø_n(n)为其第n个数的序列。

换句话说，β是翻转0和1后得到的对角线。

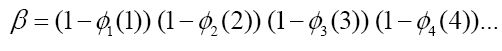
Since β is computable, there exists a number K such that 1 - ø_n(n) = ø_K(n) all n.

由于β是可数的，则存在数K，使得1 - ø_n(n) = ø_K(n)对任意n成立。

即对于某个K，在所列举的可计算数中存在α_K，使得

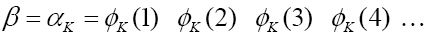
一般地， 对于n, 有。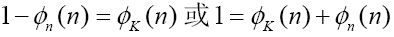

图灵的反对者使用这一算术论据来证明β不可能存在：

Putting n=K,

令，n=K,

即。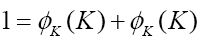

we have 1 = 2ø_K(K), i.e. 1 is even. This is impossible. The computable sequences are therefore not enumerable."

我们有1=2ø_K(K)，即1是偶数。而这是不可能的，因此可计算序列是不可数的。”

这相当有趣，这位神秘的反对者描述了如何基于所枚举的可计算序列计算一个称为β的数，而这个可计算数并不在所枚举的序列中。因此，反对者声称，可计算序列是不可数的。

但是图灵很冷静，他说：

The fallacy in this argument lies in the assumption that β is computable.

这个证明的谬误在于假设β是可计算的。

谬误？什么谬误，β怎能是不可计算的？β是由可计算序列的枚举计算得到的，那么它必然是可计算的，不是吗？

好吧，其实不是的。

让我们退一步看，图灵最初将可计算数定义为那些可以用有限方法计算的数。他建造了虚构的机器来计算这些数，并说明每台机器都可被一个称为描述数的正整数唯一标识。因为整数是可数的，图灵机是可数的，所以可计算序列是可数的。

在某种意义上，可以像枚举正整数一样简单地枚举图灵机：

1

2

3

4

5

…

所有的图灵机都将出现在描述数的列表中，并且可以从描述数中得到标准描述，这样我们可将其提供给通用机来取得可计算序列。

当然，我们还是遗漏了一些东西：我们没有方法来精确地确定列表里的哪些正整数是非循环机的描述数。

想想第2节中的定义，非循环机是指永远不停地打印0和1的机器。虽然一个永不停歇的机器看起来像是“失去了控制”或“疯狂的”，但是非循环机对于计算无理数或者有理循环数是非常必要的，甚至对于像1这样的有理数（在二进制看来是与1/2等价的），人们更加偏向于非循环机打印1及一串连续的0，

.10000000…

另一方面，循环机指的是陷入了不期望循环的机器。例如，循环机可能在不移动读写头的情况下持续打印0，也可能持续地打印除0和1之外的符号。

术语“非循环”和“循环”并非最佳的描述用语，非循环机可能无止境地处于打印0或1的小循环中，这是没问题的。而循环机可能由于转向一个不存在的m-格局而阻塞，这只是循环机会发生的诸多问题中的一种。

我们需要确定非循环机的描述数，因为它们是唯一能被通用机解释的。我们可能已经成功枚举了所有的图灵机（在正整数的区间中），但是还未确认它们是非循环的，因此不能用它们来生成可计算序列。

显然，许多整数不是机器的描述数。无论如何，我们可以很容易地确定（通过人工观测或图灵机）某个整数是不是一个结构良好的描述数，即它可以分割成结构良好的指令集，任一指令都以m-格局作为开始。我们甚至可以确定一个机器是否引用了不存在的m-格局，同时容易地检查某个m-格局是否包含了打印0或1的指令。通过这样的过程，我们可以知道最小的结构良好的描述数为31 334 317，并且这是一个循环机（只打印空格）。第一个非循环机在313 324 317处出现，而到了313 325 317才出现了第一个从左往右打印的非循环机。

前两个非循环的、从左往右打印的图灵机在正整数枚举最开始时就确认了。

1

2

3

4

5

…

313 325 317 ←从左往右打印0的机器

…

3 133 225 317←从左往右打印1的机器

…

当然，这些是最最简单的机器，标识它们的方法也非常简单。更有难度的（实际上像图灵将要说明的，几乎不可能的）是，通过实现了某个通用过程的机器，来判断特定的整数是否是非循环机的描述数。

这个通用过程正是对角线方法的过程。β的每一位都基于不同的可计算数，因此计算β需要标识所有的非循环图灵机。图灵将证明，这些非循环机不能被有限方法标识，即不能明确地枚举可计算数序列，因此β便不是一个可计算序列。

It would be true if we could enumerate the computable sequnces by finite means, but the problem of enumerating computable sequences is equivalent to the problem of finding out whether a given numer is the D.N of a circle-free machine, and we have no general process for doing this in a finite number of steps.

如果我们能够用有限步骤枚举可计算序列，那它便是成立的。然而，枚举可计算序列的问题和找出给定的数是否是非循环机的标准描述的问题是等价的，而我们没有任何通用过程能够在有限步内处理这一问题。

图灵微妙地转移了焦点。他试图从将康托尔的对角证明法应用到可计算序列开始，然而现在，他只是想要讨论在试图标识所有非循环机的描述数时会发生什么。

In fact, by applying the diagnoal process argument correctly, we can show that there cannot be any such general process.

实际上，通过正确地使用对角线法，我们能够证明不存在任何这样的通用过程。

如果像图灵断言的那样，没有任何通用过程用于确定某个整数是否是非循环机的描述数，那么β是不可计算的。这就使得反对者所谓的可计算序列不可数的证明无效了。没有什么可以削弱我们对于可计算序列实际上是可数的信心，这也就表明了可计算数无法包含所有实数。

遗憾的是，图灵在下一段的开始说得非常含糊：

The simplest and most direct proof of this is by showing that, if this general process exists, then there is a machine which computes β.

关于这个命题最简单、最直接的证明是，说明如果存在这样的通用过程，那么就存在一台可以计算β的机器。

我认为他的意思是，不可能存在通用过程来确定某台机器是非循环机，因为如果存在，我们就能够计算β。而现在我们知道不可能计算β，否则对角证明法就有效了，于是可计算序列将是不可数的。

This proof, although perfectly sound, has the disadvantage that it may leave the reader with a feeling that “there must be something wrong”.

这个证明虽然看起来很完美，但有个缺点，它很可能使读者产生“一定有什么地方出了问题”的想法。

这个悖论始终与我们的直觉格格不入，因此，图灵将要用更直接的方法来证明，并不存在一个机器能够确定某个正整数是非循环机的描述数。

The proof which I shall give has not this disadvantage, and gives a certain insight into the significance of the idea “circle-free”.

我将要给出的证明没有这方面的问题，同时会给出“非循环”这一概念更为明确的见解。

他可能在这个数论的小小练习中引入了更为深远的东西。

现在图灵想要的是一台能从可计算序列中得到一个数位的机器，他不需要考虑减去这一数位。实际上，图灵试图计算一些比β简单得多的东西。

It depends not on constructing β, but on constructing β′, whose n-th figure is ø_n(n).

它并不依赖于β的构造，而是依赖β′的构造，这里β′的第n个量是ø_n(n)。

在图灵论文的开始（本书第57页），他说：“尽管如此，可计算数并不完全包括所有可定义的数，我们将给出一个可定义的不可计算的数。”β和β′都是可定义的数。β′可定义，是由于我们可以给出如何计算它的指令：从1开始枚举所有的数。对每一个数，判断它是否是一个结构良好的图灵机的描述数；如果是，判断这个机器是否是非循环的；如果是，计算这个数直到它的第n位（这里n是在当前所计的非循环机的标识加上1），这一位就是β′的第n位。

可以看到，β′是完全可定义的，但是它是否可计算呢？

图灵没有给出任何终止机器的指令，他所面对的问题在现在称为终止问题（halting problem，最早在马丁·戴维斯1958年的书《可计算性和不可解性》中提及^［33］）。我们是否能够定义一个图灵机，使其能够确定另一个图灵机会停止还是永久运行下去？如果用循环的想法代替终止，仍存在同样的问题。一台图灵机能否分析另一台图灵机，并确定它最终的命运？

图灵一开始假设存在一台可以判断任意机器是否是非循环机器。在下面的讨论中，他使用机器的标准描述代替了描述数，这并不重要，二者总是可以转换的。

[247]

Let us suppose that there is such a process; that is to say, that we can invent a machine which, when supplied with the S.D of any computing machine will test this S.D and if is circular will mark the S.D with the symbol “u” and if it is circle-free will mark it with “s”

我们假设存在这样一个过程，就是说，我们可以发明一台机器，当提供了任一机器的标准描述，它能够检测这个标准描述。如果是循环机，则用符号u标记这个标准描述；如果是非循环机，则用符号s 标记这个标准描述。

机器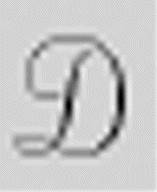是决策机，符号u表示不符合要求（即循环机），s表示符合要求（非循环机）。图灵在第5节的结尾定义了这些术语（图灵论文第241页，本书第129页）。

By combining the machines and we could construct a machine to compute the sequence β′.

结合机器和，我们可以构造机器来计算序列β′。

实际上，机器仍需要生成正整数，并将其转化成标准描述，而这些工作都很琐碎。对于机器生成的每一个正整数，用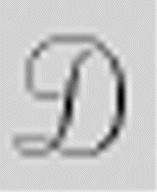来决定这个数是否定义了一个符合要求的机器。如果是，则将标准描述传输给通用机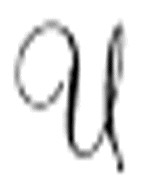来计算该序列。对第n个可计算序列，只需要运行机器至第n位。该位稍后将变成β′的第n位。因为机器受机器控制，当获得所需的特殊数位后便可终止。

对来说，有必要事先检查机器的标准描述，因为我们不希望由于运行了不符合要求机器而卡住。如果传递给一个不符合要求机器的标准描述，则不符合要求机器将无法打印任何数字位，整个进程将卡在这里而无法继续。

图灵实际上没有真正描述这个具有魔力的决策机会是什么样子，因此这可能存在一个巨大的暗示：不存在这种机器。下意识地想想，它至少是非常困难的。除了模拟目标机器并追踪它的每一步，机器如何能够确定一个机器是非循环的呢？

无论如何，机器和在处理标准描述（与描述数等价）上是相似的，都是在纸带上编码。

The machine may require a tape. We may suppose that it uses the E-squares beyond all symbols on F-squares, and that when it has reached its verdict all the rough work done by is erased.

机器需要一条纸带。我们假设它使用了F-格上所有符号之外的E-格，并在最后得出结论时，抹去机器所做的中间工作。

只有符号s或u作为最终判断结果留了下来。

The machine has its motion divided into sections. In the first N - 1 sections, among other things, the integers 1, 2,…,N - 1 have been written down and tested by the machine.

机器的操作分成几个部分。在前N-1部分中，处理其他事情的同时，机器写下整数1，2，…，N-1并加以检测。

这里“分成几个部分”并不意味着机器存在不同的部分来处理不同的数。对应于每个数的不同的格局，都要求是无限的。在一段时间内，图灵考虑了顺序性的操作。实际的过程必须对所有整数都是通用的：机器一个接一个地产生正整数，并将其按顺序传递给以决定它是否是符合要求的集合，如果是，用机器来计算可计算序列中的某一些数位。

A certain number, say R(N - 1), of them have been found to be the D.N's of circle-free machines.

其中已发现有R(N-1)个数是非循环机的描述数。

R只表示已经被计数的非循环机。机器需要R来确定对于将要出现的非循环机需要计算多少位。

In the N-the section the machine tests the number N. If N is satisfactory, i.e., if it is the D.N of a circle-free machine, then R(N) = 1 + R(N - 1) and the first R(N) figures of the sequence of which a D.N is N are calculated.

在第N部分中，机器检测数N。如果数N是可接受的，即它是非循环机的描述数，则R(N)=1+R(N-1)，并且将计算描述数为N的序列的前R(N)个数字。

举例来说，如果N是3 133 225 317，则R(N)为1（参见之前列出的关于前两个符合要求机器所对应的正整数）。到目前为止，只发现了一个符合要求机器。机器将确定N确实是非循环机的描述数，因此R(N)设为2，机器计算由3 133 225 317定义的机器的前两位，这两位都是1。用这些数位的第二个作为β′的第二位，依此类推即可！

The R(N)-th figure of this sequence is written down as one of the figures of the sequence beta;′ computed by

通过H的计算，这个序列的第R(N)个数字将被写为序列β′的一位。

当然，一般情况是，数N根本不是机器或循环机的描述数。

If N is not satisfactory, then R(N) = R(N - 1) and the machine goes on to the (N + 1)-th section of its motion.

如果N是不可接受的，则R(N)=R(N-1)，机器转向第N+1个部分继续运行。

要点在于，机器必须一个接一个地检测可能的描述数，并且对于每一个可接受的描述数，机器都必须运行至第R(N)位。

图灵花费了很大力气来证明是非循环的。由初始假设，是非循环的，而只是简单地对每个可能的描述数运行。

From the construction of we can see that is circle-free. Each section of the motion of comes to an end after a finite number of steps. For, by our assumption about , the decision as to whether N is satisfactory is reached in a finite number of steps. If N is not satisfactory, then the N-th section is finished. If N is satisfactory, this means that the machine (N) whose D.N is N is circle-free, and therefore its R(N)-th figure can be calculated in a finite number of steps. When this figure has been calculated and written down as the R(N)-th figure of β′, the N-th section is finished. Hence is circle-free.

从的构成可以看出，是非循环的。的每一部分操作都在有限步内终止。由我们关于的假设，可在有限步内判定N是否是可接受的。如果N是不可接受的，那么第N部分终止；如果N是可接受的，意味着描述数是N的机器是非循环的，因此第R(N)个数字可在有限步内计算得到。当这个数字被计算出并写为β′的第R(N)个数字时，第N部分终止，所以是非循环的。

是一个图灵机，所以有一个描述数（图灵称之为K）。从某种程度讲，必须处理它自己的描述数，即需要确定它本身是否是非循环的。

Now let K be the D.N of . What does do in the K-th section of its motion? It must test whether K is satisfactory, giving a verdict “s” or “u”. Since K is the D.N of and since is circle-free, the verdict cannot be “u”

令K为的描述数，在第K部分的操作会是怎样的呢？它必须检测K是否可接受，给出一个判定符号s或u。因为K是的描述数，而是非循环机，所以判定结果不可能是u。

图灵又说：

On the other hand the verdict cannot be “s”.

另一方面，判定结果也不可能是s。

根本的问题在于，陷入了无限循环中。在计数到数字K（它自身的描述数）之前，已经分析了1到K-1的所有正整数。非循环机的数目在此时为R(K-1)，并且β′的前R(K-1)位已经计算出来了。

β′的第R(K)位是什么呢？为了得到这一位，必须追踪它自己的操作，这意味着它不得不复制它计数到K之前的所有操作，然后再重新开始这个过程。这就是不可能是非循环的原因。

For if it were, then in the K-th section of its motion would be bound to compute the first R(K - 1) + 1 = R(K) figures of the sequence computed by the machine with K as its D.N and to write down the R(K)-th as a figure of the sequence computed by . The computation of the first R(K) - 1 figures would be carried out all right, but the instructions for calculating the R(K)-th would amount to “calculate the first R(K) figures computed by H and write down the R(K)-th”. This R(K)-th figure would never be found.

因为如果是s，那么机器的第K部分操作将一定要计算以K为描述数的机器所产生序列的前R(K-1)+1=R(K)个数字，并将第R(K)个数写下来作为计算的序列的数字。前R(K-1)个数字的计算不会有问题，但是计算第R(K)个数字的指令相当于“计算由H计算的前R(K)个数字，并写下第R(K)个数字”，这样的第R(K)个数字永远不会找到。

（倒数第二行的H应该是。）

基于其他机器产生的序列，生成了一列数位。这很直接，我们可以想象成这是一个正在产生1/3、π、2的平方根的二进制序列的机器，但是如何获得这个生成的序列里的第K位呢？这需要它从自身获得这一位，但是这不可能，因为只能从其他机器获得数位。

所以，当遇到它的描述数时有了点麻烦。就不能忽略它吗？可以，但是我们会发现，每个可计算序列都可以用不同的机器来计算。这些机器用不同的方式计算相同的序列，或者它们还有一些不必要的指令。可能也需要跳过这些类似的机器。不能计算β′但能计算接近β′的数，比如交换了β′的第27位和第54位，这样的机器又如何？这样的机器有无数个，必须防止它们给带来负担——一个无法完成的负担。

I.e., is circular, contrary both to what we have found in the last paragraph and to the verdict “s”. Thus both verdicts are impossible and we conclude that there can be no machine .

换言之，是循环的，这和我们在上一段的结论以及断言s都是相反的。因此这些断言都是不可能的，我们可以总结出没有机器。

没有通用过程来判断一台机器是否是非循环的。这就是说，没有这样的计算机程序，可以决定其他计算机程序的最终命运。

图灵也解决了对角线法的矛盾。他首先指出可计算数是可数的，而对角线法似乎表明你可以创造一个不在列表中的可计算数。图灵证明了对角线法是无法通过有限步计算的，因此它不可计算。可计算数可能是可数的，但它们实际上不能在有限步内被枚举出来。

图灵没有这样结束这一节。他假设了一个机器，可能表示“过去的输出”。

[248]

We can show further that there can be no machine which, when supplied with the S.D of an aribtrary machine , will determine whether ever prints a given symbol (0 say).

我们可以进一步证明，没有这样的机器，当给它提供了任意一台机器的标准描述时，它可以判断是否曾经打印过给定的符号（比如0）。

在论文的最后一节，图灵需要机器来证明判定性问题是无解的。这里，他将证明机器是不存在的：首先如果机器存在，那么就存在一个过程来判断机器是否经常无限次打印0，但这又意味着存在一个类似的过程来判断机器是否经常无限次打印1。如果你有能力来判断机器是经常无限次打印0还是经常无限次打印1（或者都打印），那么你就有能力判断机器是否是非循环的。这样的过程已经被证明是不存在的，所以机器也一定不存在。

We will first show that, if there is a machine , then there is a general process for determining whether a given machine prints 0 infinitely often.

我们首先证明，如果存在这样的机器，就会有一个通用过程来判定机器是否经常无限次打印0。

图灵通过定义任意机器的变体这一古怪的方法，来对此进行判断。

Let ₁ be a machine which prints the same sequence as , except that in the position where the first 0 printed by stands, ₁ prints . ₂ is to have the first two symbols 0 replaced by , and so on. Thus, if were to print

ABA01AAB0010AB…,

then ₁ would print

and ₂ would print

假设机器₁打印的序列与机器打印的序列相同，所不同的只是，在打印第一个0的地方，₁打印；₂将头两个符号0替换成，以此类推。这样，如果打印

ABA01AAB0010AB…，

那么₁会打印

₂会打印

如果你有一台机器，就能定义一台机器读取的标准描述，然后计算₁、₂等的标准描述吗？图灵说可以，他称这样的机器为。

Now let be a machine which, when supplied with the S.D of , will write down successively the S.D of , of ₁, of ₂ … (there is such a machine).

假设有一台机器，当给它提供了的标准描述后，它就可以连续写出的标准描述，₁的标准描述，₂的标准描述……（这样的机器是存在的。）

为了让我们自己相信似乎是可信的，我们考虑一台非常简单的机器，它选择性地打印0和1，即1/3的二进制格式但不跳过任何空间：

这是机器。下面是机器₁：

所有的初始格局（包括和₁）都只是简单的重复，然后给出不同的m-格局。在第一组格局中，所有应该打印0的地方现在打印，然后它会跳到第二组合适的格局中。₂有三组：

你可能注意到，这些修改过的机器永远不会遇到格局q₂，但是对于这台机器，这是偶然的。

因此，存在是完全可信的。注意这些机器之间的关系：如果从来不打印0，那么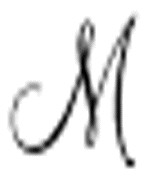₁、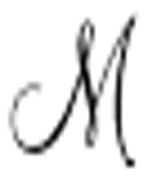₂等也不会。如果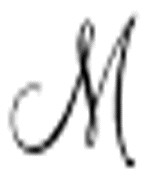只打印一次0，那么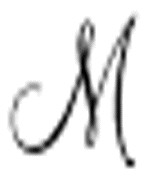₁、₂等永远不会打印0。如果打印了0两次，那么₁打印0一次，而₂等永远不会打印0。如果经常无限次打印0，那么₁、₂等也会如此。

现在回忆一下机器，它被假设可以判断一个机器是否打印过0。

We combine with and obtain a new machine, . In the motion of first is used to write down the S.D of , and then tests its, :0: is written if it is found that never prints 0; then writes the S.D of ₁, and this is tested, :0: being printed if and only if ₁ never prints 0, and so on.

我们将机器和机器合并为一个新的机器。的第一个动作就是使用写下的标准描述，然后让来测试它。如果从未打印0，那么写下:0:。然后写下₁的标准描述，再进行测试。仅当₁从未打印0时才写下:0:。如此一直继续下去。

使用来生成、₁、₂等的描述数，然后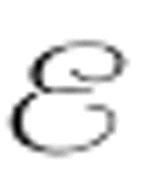来判断产生结果的机器是否打印过0。如果它从未打印过0，那么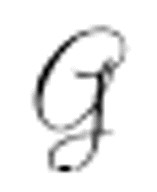打印0。

结果是这样的：如果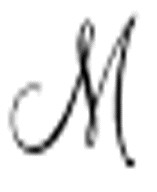从未打印过0或仅有限次打印0，那么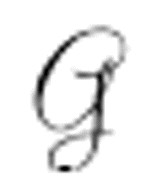经常无限次打印0。如果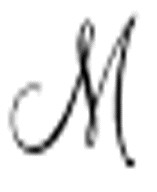经常无限次打印0，则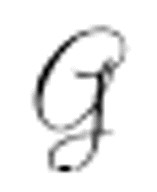不打印0。

Now let us test with . If it is found that never prints 0, then prints 0 infinitely often; if prints 0 sometimes, then does not print 0 infinitely often.

现在，我们用来测试。如果发现从未打印过0，那么经常无限次打印0；如果有时打印0，那么不经常无限次打印0。

这意味着，可以告诉我们是否经常无限次打印0。这是通过它自己不打印0来告诉我们的。

Similarly there is a general process for determining whether prints 1 infinitely often. By a combination of these processes we have a process for determining whether prints an infinity of figures, i.e. we have a process for determining whether is circle-free. There can therefore be no machine .

类似地，也有一个方法来判断是否经常无限次打印1。通过将这些过程结合起来，我们有了一个过程来判断是否无限次打印一个数字。也就是，我们可以有一个过程来判断是否是非循环的。所以不会存在这样的机器。

图灵也给出了另一个反证法来证明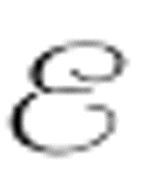并不存在。因为它最终会导致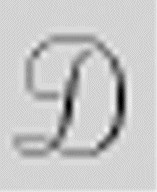存在——机器可以判断其他机器是否是非循环的，而事实上，这种机器不存在。

图灵在结束这一节时提醒道，我们真的需要检查人类计算者和图灵机是等价的这一假设，因为我们在很大程度上依赖于此。

The expression “there is a general process for determining …” has been used throughout this section as equivalent to “there is a machine which will determine …”. This usage can be justified if and only if we can justify our definition of “computable”.

本节中使用的“有一个通用过程来判断……”的表述。等价于“有这样一台机器能判断……”。这种用法可以证明是对的，当且仅当我们可以证明“可计算”的定义。

这个证明将在下一节讨论。

图灵然后略微提及了这个证明的另一个方面，这些内容将在本书第三部分介绍。图灵将图灵机的输出释义为“可计算数”，而图灵机在这方面具有更多的灵活性。例如输出如下序列的机器：

0011010100010100010100010000010…

这看起来像是一个数，实际上，这是一个“素数”机器的输出，我们将这样的数记为IsPrime(n)。对于该序列的第n个数字（n从0开始），如果n是素数，则IsPrime(n)的值为1，否则IsPrime(n)的值为0。这台机器输出的序列表明了2、3、5、7、11、13、17、19、23和29都是素数。这样的机器似乎完全可信，但是它并不是真正对某个数字进行计算，而是告诉我们一些自然数的信息。

For each of these “general process” problems can be expressed as a problem concerning a general process for determining whether a given integer n has a property G(n) [e.g. G(n) might mean “n is satisfactory” or “n is the Gödel representation of a provable formula”], and this is equivalent to computing a number whose n-th figure is 1 if G (n) is true and 0 if it is false.

每一个这样的“通用过程”问题都能表示成，判定给定整数n是否具有性质G(n)（如G(n)表示“n是可接受的”或者“n是可证明公式的哥德尔表示”）的通用过程，并且等价于计算一个数，如果G(n)成立，则这个数的第n个数字为1，否则为0。

现在，图灵似乎将他的计算机器和数理逻辑联系在了一起，这种联系本书在第三部分提及。符号0和1不仅仅可以是二进制位，同时还可用来表示真或假，就像乔治·布尔多年前认识到的那样。

考虑一组关于自然数的函数，它们会返回真或假（1或0）。

IsPrime(n)

IsEven(n)

IsOdd(n)

IsLessThanTen(n)

IsMultipleOfTwentyTwo(n)

它们有时称为布尔函数，可以通过由图灵机对n=0, 1, 2, 3…输出0和1的序列来实现，其中判定奇数的函数IsOdd输出的序列与图灵第一台样机输出的序列交替相同。

图灵已经说明了这些可计算序列是可数的，因此和它们的名字一样，它们可以按字母排序，例如在康托尔关于超限数的记号中，自然数的所有可计算、可按字母排序的布尔函数集的势为，和可数集的势相同。

每个布尔函数都会针对自然数的子集返回真或者1。例如，IsPrime针对下列的自然数集合返回1：

{2, 3, 5, 7,11,13,…}

每个这样的布尔函数都和不同的自然数集合相关联。可以回想一下第2章，所有子集的集合叫做超集，如果原始集合的势是，那么这个超集的势就是。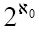

所有可想到的布尔函数的集合的势是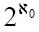，而所有可计算布尔函数（其实就是所有可以用英语名字描述的布尔函数的集合）的势是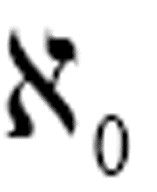。这是可想到的和可计算的之间的另一个重大鸿沟。