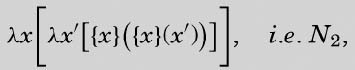λxyM

来表示。

克莱尼于1935年改写并发表了他的博士论文“形式逻辑的正整数理论”，^［11］该论文分为两部分。阅读这篇论文之前要先看邱奇的两篇论文以及克莱尼之前的论文，其第二部分也提及了即将发表的邱奇和罗瑟合作的论文。^［12］

尽管由邱奇、克莱尼、罗瑟一起发明的λ演算相当全面，既涉及逻辑又涉及算术，但是这里我只想集中探讨一些基本的算术，这样你就可以看到，如何通过单纯的字符运算来实现加法和乘法了。

定义自然数时，我们总是需要从0或1开始。邱奇和克莱尼是以1开始的，下面就是其符号：^［13］

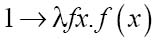
这里箭头的意思是“代表”或“全称是”。这个公式看起来似乎有点怪，实际上可能看起来是非常怪，但这仅仅是一个定义，所以现在还没必要追究其意义。更冗长的版本是

因此，1实际上是一个含有两个自变量f和x的函数，非常唐突，定义一个数字居然需要额外多出的两个变量。

下面的是后继函数：

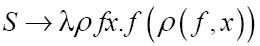
还是很奇怪吧，我也这么认为。尽管我们希望后继函数中包括自变量，但不希望其中包含3个自变量。

幸运的是，符号2可以定义成你期望的形式：

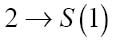
如果我们事实上想对1应用后继函数，就必须保证所有的自变量都是唯一的，因此要使用下面1的等价表达式：

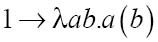
当使用λ表达式时，函数和变量经常互换角色。在下面变换后的公式的推导过程中，我选择性地使用花括号来标记将要在那一步被替换的包含一个自变量的函数。

函数S(1)也可以写为{S}1或者：

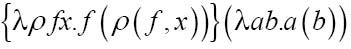
后继函数的第一个自变量为ρ，因此用1的表达式将函数中的ρ替换掉，λ后的ρ就消失了：

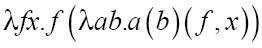
现在这个公式包含另一个函数，该函数中含有两个参数：

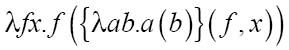
用f替换a，x替换b：

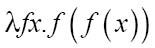
这样就完成了。

尽管1最初定义为：

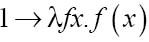
数字2定义为：

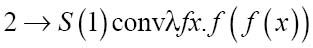
比较转换后的2和1的表达式，你会发觉在点的右侧多出一个f和一对括号。现在使用不同的变量λab.a(a(b))来表示2，并尝试确定下一个后继数{S}(2):

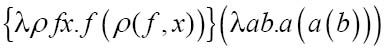
同样，用2来替代ρ：

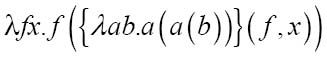
用f替换a，x替换b：

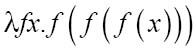
这是3的λ表达式。我猜你开始明白这个模式了，我们最想从正整数的抽象表达式中得到的是某种后继性。下面这个记号表明了这一后继性：每一个后继整数都会增加对第一个自变量的嵌套。

克莱尼定义“加”运算为：

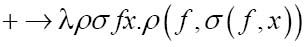
有点怀疑了吧？我们试着将2和3相加。首先我们需要使所有的自变量不同。我将使用λab.a(a(b))代表2，λcd.c(c(c(d)))代表3，因此{+}(2,3)就是：

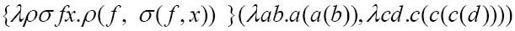
在+函数中，用2的公式替换ρ，用3的公式替换σ：

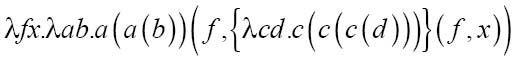
替换后的3是一个函数，其中用f替换c，x替换d：

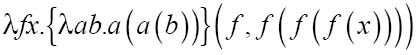
现在替换后的2是一个用f替代a，用f(f(f(x)))替代b的函数：

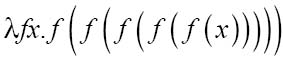
到这里，我们就完成了运算。答案与S(S(S(S(1))))-致，也就是5。

有意思的是，乘法函数比加法函数还要简单：

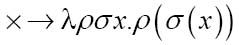
我们来计算2和3的乘法，可以将{×}(2,3)写成：

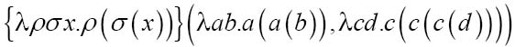
用2的公式替换ρ，3的公式替换σ：

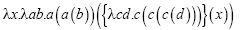
现在3变成一个用x替代c的函数：

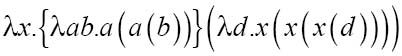
现在2变成一个函数，用右侧的表达式替换a：

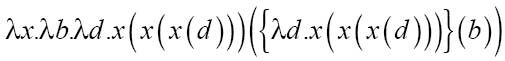
在右侧的函数，用b替换d

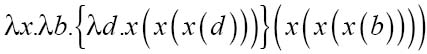
最后替换d：

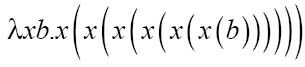
这就是6，当然也是2与3相乘的结果。

这些数字的函数定义可以让你做一些比较奇怪的事情，例如

{2}(3）

即：

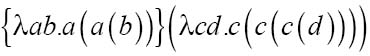
在你完成了所有费力的替换后，最后会得到：

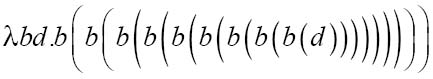
也就是9，毫无意外，这就是3的二次方。这也就是为什么m的n次方定义为：

λmn.nm

在这个系统中，乘比加看起来要简单，指数形式是其中最简单的。当邱奇、克莱尼和罗瑟使用λ演算做实验时，他们发现λ表示法可以表示任何他们能想到的东西，这是后来称为λ可定义性的性质。“邱奇一直在推断，并最后明确地提出，λ可定义函数是所有的有效可计算函数。”^［14］

库尔特·哥德尔在1933年来到高级研究院。1934年春，他在普林斯顿讲授他的不完备性定理及递归函数，递归函数是从基本原始函数发展出来的。^［15］ 让哥德尔对递归函数感兴趣的是雅克·赫尔布兰德（1908—1931）在1931年写给他的信，这位年轻聪明的法国数学家在攀登阿尔卑斯山时意外身亡了。

尽管如此，哥德尔在那时仍然坚信，λ函数和递归函数都不足以包含所有我们认为的非正式有效可计算性。

1936年，邱奇发表了“初等数论的不可解问题”^［16］，在这篇文章中首次出现了“λ可定义”一词。（之前，克莱尼在使用lambda记号表示逻辑和算术运算时仅仅使用了“可定义”或者“形式可定义”。）邱奇引用了自己之前的论文、克莱尼的两篇论文，以及克莱尼即将发表的探讨递归函数和λ可定义函数之间关系的论文。^［17］与哥德尔构造了一个不可判定的命题一样，邱奇使用哥德尔的记数法同样构造了一个不可解的问题。

在此基础上，邱奇在《符号逻辑期刊》（他自己也是该期刊的编辑）的首版上发表了两页的“判定性问题的笔记”，他在结论中写道：“判定性问题的通用情况是不可解的。”^［18］这篇文章是在1936年4月15日被杂志接收的，比图灵在1936年5月28日提交到伦敦数学学会的文章早了6周。

1936年夏，图灵可能花了大部分时间阅读我之前提到的邱奇和克莱尼的文章，学习λ演算，并验证它如何与自己的计算机器相关联。据显示，图灵的三页附录在8月28日被伦敦数学学会接收。图灵在最后写上了：“美国新泽西州普林斯顿大学研究生院。”他很期待自己的新家。直到9月23日，他才离开英国前往美国，在29日到达纽约。^［19］

Added 28 August, 1936.

APPENDIX.

Computability and effective calculability

The theorem that all effectively calculable (λ-definable) sequences are computable and its converse are proved below in outline.

1936年8月28日新增

附录

可计算性和有效可计算性

所有的有效可计算（λ可定义）序列都是可计算的，反之也成立。这个定理的证明将在下面简略给出。

在这里，“简略”的意思是证明中会跳过一些步骤。

It is assumed that the terms “well-formed formula”（W.F.F.) and “conversion” as used by Church and Kleene are understood. In the second of these proofs the existence of several formulae is assumed without proof; these formulae may be constructed straightforwardly with the help of, e.g., the results of Kleene in “A theory of positive integers in formal logic”, American Journal of Math., 57 (1935), 153-173, 219-244.

假设人们已经理解了邱奇和克莱尼所使用的“合式公式”（W.F.F.）和“转换”这些术语。在第二个证明中，我们假定了一些公式已经存在，不再证明。这些公式可以参考克莱尼的论文“形式逻辑的正整数理论”[发表在《美国数学杂志》57（1935），153-173，219-244]直接构造。

图灵这里说的“第二个证明”是指上述定理的逆命题：每一个可计算序列同样也是λ可定义的。

The W.F.F. representing an integer n will be denoted by N_n.

表示一个整数n的W.F.F.将记为N_n。

我们开始使用克莱尼对1和后继数字的定义，但要使这些自变量与图灵后面使用的保持一致，N₁是，λxy.x(y), N₂是λxy.x（x(y)), N_n是λxy.x(x(x(x…(y)…))).

We shall say that a sequence γ whose n-th figure is φ_γ(n) is λ-definable or effectively calculable if 1 + φ_γ(u) is a λ-definable function of n,

如果1+φ_γ(u)是n的λ可定义函数，我们就称第n个数字为φ_γ (n)的序列γ是λ可定义的或者是有效可计算的。

φ_r两次出现时的参数都应该是n，而不是u，因此表达式应该是1+φ_γ(n)。可计算序列γ的第n位是0或者1，但邱奇和克莱尼定义的λ演算只考虑了正整数，并不包括0。φ_γ(n)并不是λ可定义的，因为0不是λ可定义的。所以，数字都加上1变成1和2。

i.e. if there is a W.F.F.

M_γ such that, for all integers n, {M_γ}(N_n) conv N_φγ(n)+1,

i.e.{M_γ}(N_n) is convertible into λxy.x(x(y)) or into λxy.x(y) according as the n-th figure of λ is 1 or 0.

如果存在W.F.F. M_γ，使得对于所有的整数n，

{M_γ}(N_n)convN_φγ(n)+1,

即根据λ的第n位数是1还是0，{M_γ}(N_n) 可以转换为λxy.x(x(y))或者。λxy.x(y).

最后一行的λ其实是错的，应该是“γ的第n位数”。根据对应的数字是1还是0，值N_n（指序列中的数字位）处的函数M_γ可转换为 λxy.x(x(y))（也就是2）或者 λxy.x(y)（也就是1）。

例如，如果γ的第5位是1，那么φ_γ(5)是1，并且

{M_γ}(N₅) convN_φγ(5)+1

也就是说

{M_γ}(N₅) convN₂

To show that every λ-definable sequence γ is computable, we have to show how to construct a machine to compute γ. For use with machines it is convenient to make a trivial modification in the calculus of conversion. This alteration consists in using x, x′, x″, … as variables instead of a, b, c, ….

为了证明每一个λ可定义序列γ都是可计算的，我们必须首先构造一个可以计算γ的机器。使用机器，可以方便地在演算转换中进行简单的修改，这些修改包括使用x, x′, x″, … 作为变量，而不是使用a, b, c….

图灵至今还未使用任何以a、b或c命名的变量，但他使用了x和y。他希望所有的变量都具有统一的形式，因为接下来需要进行比较和匹配。这与第8节的要求很相似（本书第205页）：一阶谓词逻辑在被机器处理前需要“系统化”。

We now construct a machine which, when supplied with the formula M_γ, writes down the sequence γ. The construction of is somewhat similar to that of the machine which proves all provable formulae of the functional calculus. We first construct a choice machine ₁, which, if supplied with a W.F.F., M say, and suitably manipulated, obtains any formula into which M is convertible. ₁ can then be modified so as to yield an automatic machine ₂ which obtains successively all the formulae [264]

into which M is convertible (cf. footnote p. 252).

我们现在构造一台机器，在提供了公式M_γ时可以写下序列γ。的构造过程与在某种程度上很相似，证明了函数演算中所有可证明的公式。我们首先构造一个选择机器₁，如果给₁提供了一个W.F.F.，例如M，并合理调整，使₁包含任一M可转换到的公式，则可以调整₁使之衍生出自动机器₂，₂相继得到所有M可转换到的公式（参见第252页脚注）。

在图灵论文的第252页有5个脚注，图灵引用的是第二个（本书第205页）。在那里，他讨论了可以证明所有一阶逻辑的可证明公式的机器。考虑到λ表达式转换的系统化方式，这台机器看起来与之相似，很可能更加简单。

The machine includes ₂ as a part. The motion of the machine when supplied with the formula M_γ is divided into sections of which the n-th is devoted to finding the n-th figure of γ. The first stage in this n-th section is the formation of {M_γ}(N_n). This formula is then supplied to the machine ₂, which converts it successively into various other formulae. Each formula into which it is convertible eventually appears, and each, as it is found, is compared with