2.6　数据压缩

数据压缩分为有损压缩与无损压缩两种，有损压缩算法压缩比率高，但数据可能失真，一般用于压缩图片、音频、视频；而无损压缩算法能够完全还原原始数据，本文只讨论无损压缩算法。早期的数据压缩技术就是基于编码上的优化技术，其中以Huffman编码最为知名，它通过统计字符出现的频率计算最优前缀编码。1977年，以色列人Jacob Ziv和Abraham Lempel发表论文《顺序数据压缩的一个通用算法》，从此，LZ系列压缩算法几乎垄断了通用无损压缩领域，常用的Gzip算法中使用的LZ77，GIF图片格式中使用的LZW，以及LZO等压缩算法都属于这个系列。设计压缩算法时不仅要考虑压缩比，还要考虑压缩算法的执行效率。Google Bigtable系统中采用BMDiff和Zippy压缩算法，这两个算法也是LZ算法的变种，它们通过牺牲一定的压缩比，换来执行效率的大幅提升。

压缩算法的核心是找重复数据，列式存储技术通过把相同列的数据组织在一起，不仅减少了大数据分析需要查询的数据量，还大大地提高了数据的压缩比。传统的OLAP（Online Analytical Processing）数据库，如Sybase IQ、Teradata，以及Bigtable、HBase等分布式表格系统都实现了列式存储。本节介绍数据压缩以及列式存储相关的基础知识。

2.6.1　压缩算法

压缩是一个专门的研究课题，没有通用的做法，需要根据数据的特点选择或者自己开发合适的算法。压缩的本质就是找数据的重复或者规律，用尽量少的字节表示。

Huffman编码是一种基于编码的优化技术，通过统计字符出现的频率来计算最优前缀编码。LZ系列算法一般有一个窗口的概念，在窗口内部找重复并维护数据字典。常用的压缩算法包括Gzip、LZW、LZO，这些算法都借鉴或改进了原始的LZ77算法，如Gzip压缩混合使用了LZ77以及Huffman编码，LZW以及LZO算法是LZ77思想在实现手段的进一步优化。存储系统在选择压缩算法时需要考虑压缩比和效率。读操作需要先读取磁盘中的内容再解压缩，写操作需要先压缩再将压缩结果写入到磁盘，整个操作的延时包括压缩/解压缩和磁盘读写的延迟，压缩比越大，磁盘读写的数据量越小，而压缩/解压缩的时间也会越长，所以这里需要一个很好的权衡点。Google Bigtable系统中使用了BMDiff以及Zippy两种压缩算法，它们通过牺牲一定的压缩比换取算法执行速度的大幅提升，从而获得更好的折衷。

1.Huffman编码

前缀编码要求一个字符的编码不能是另一个字符的前缀。假设有三个字符A、B、C，它们的二进制编码分别是0、1、01，如果我们收到一段信息是01010，解码时我们如何区分是CCA还是ABABA，或者ABCA呢？一种解决方案就是前缀编码，要求一个字符编码不能是另外一个字符编码的前缀。如果使用前缀编码将A、B、C编码为：

A：0　B：10　C：110

这样，01010就只能被翻译成ABB。Huffman编码需要解决的问题是，如何找出一种前缀编码方式，使得编码的长度最短。

假设有一个字符串3334444555556666667777777，它是由3个3，4个4，5个5，6个6，7个7组成的。那么，对应的前缀编码可能是：

1）3:000　4:001　5:010　6:011　7:1

2）3:000　4:001　7:01　5:10　6:11

第1种编码方式的权值为（3+4+5+6）3+71=61，而第2种编码方式的权值为（3+4）3+（5+6+7）2=57。可以看出，第2种编码方式的长度更短，而且我们还可以知道，第2种编码方式是最优的Huffman编码。Huffman编码的构造过程不在本书讨论范围之内，感兴趣的读者可以参考数据结构的相关图书。

2.LZ系列压缩算法

LZ系列压缩算法是基于字典的压缩算法。假设需要压缩一篇英文文章，最容易想到的压缩算法是构造一本英文字典，这样，我们只需要保存每个单词在字典中出现的页码和位置就可以了。页码用两个字节，位置用一个字节，那么一个单词需要使用三个字节表示，而我们知道一般的英语单词长度都在三个字节以上。因此，我们实现了对这篇英文文章的压缩。当然，实际的通用压缩算法不能这么做，因为我们在解压时需要一本英文字典，而这部分信息是压缩程序不可预知的，同时也不能保存在压缩信息里面。LZ系列的算法是一种动态创建字典的方法，压缩过程中动态创建字典并保存在压缩信息里面。

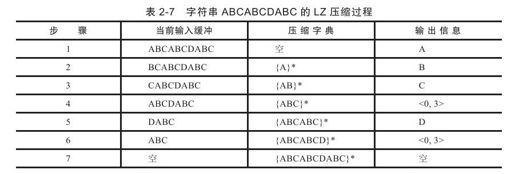
LZ77是第一个LZ系列的算法，比如字符串ABCABCDABC中ABC重复出现了三次，压缩信息中只需要保存第一个ABC，后面两个ABC只需要把第一个出现ABC的位置和长度存储下来就可以了。这样，保存后面两个ABC就只需要一个二元数组＜匹配串的相对位置，匹配长度＞。解压的时候，根据匹配串的相对位置，向前找到第一个ABC的位置，然后根据匹配的长度，直接把第一个ABC复制到当前解压缓冲区里面就可以了。

如表2-7所示，{S}表示字符串S的所有子串构成的集合，例如，{ABC}是字符串A、B、C、AB、BC、ABC构成的集合。每一步执行时如果能够在压缩字典中找到匹配串，则输出匹配信息；否则，输出源信息。执行第1步时，压缩字典为空，输出字符'A'，并将'A'加入到压缩字典；执行第2步时，压缩字典为{A}*，输出字符'B'，并将'B'加入到压缩字典；依次类推。执行到第4步和第6步时发现字符ABC之前已经出现过，输出匹配的位置和长度。

LZ系列压缩算法有如下几个问题：

1）如何区分匹配信息和源信息？通用的解决方法是额外使用一个位（bit）来区分压缩信息里面的源信息和匹配信息。

2）需要使用多少个字节表示匹配信息？记录重复信息的匹配信息包含两项，一个是匹配串的相对位置，另一个是匹配的长度。例如，可以采用固定的两个字节来表示匹配信息，其中，1位用来区分源信息和匹配信息，11位表示匹配位置，4位表示匹配长度。这样，压缩算法支持的最大数据窗口为2¹¹=2048字节，支持重复串的最大长度为2⁴=16字节。当然，也可以采用变长的方式表示匹配信息。

3）如何快速查找最长匹配串？最容易想到的做法是把字符串的所有子串都存放到一张哈希表中，表2-7中第4步执行前哈希表中包含ABC的所有子串，即A、AB、BC、ABC。这种做法的运行效率很低，实际的做法往往会做一些改进。例如，哈希表中只保存所有长度为3的子串，如果在数据字典中找到匹配串，即前3个字节相同，接着再往后顺序遍历找出最长匹配。

3.BMDiff与Zippy

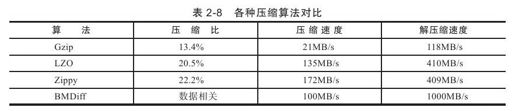
在Google的Bigtable系统中，设计了BMDiff和Zippy两种压缩算法。BMDiff和Zippy（也称为Snappy）也属于LZ系列，相比传统的LZW或者Gzip，这两种算法的压缩比不算高，但是处理速度非常快。如表2-8所示，Zippy和BMDiff的压缩/解压缩速度是Gzip算法的5～10倍。

相比原始的LZ77，Zippy实现时主要做了如下改进：

1）压缩字典中只保存所有长度为4的子串，只有重复匹配的长度大于等于4，才输出匹配信息；否则，输出源信息。另外，Zippy算法中的压缩字典只保存最后一个长度等于4的子串的位置，以ABCDEABCDABCDE为例，Zippy算法的过程参见表2-9。

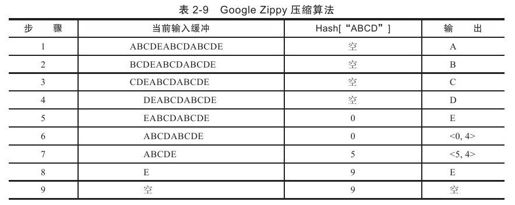
Zippy算法执行完第4步后，发现"ABCD"出现过，于是在压缩字典中记录"ABCD"第一次出现的位置，即位置0。执行到第6步时发现ABCD之前出现过，输出匹配信息，同时将数据字典中记录的ABCD的位置更新为第二个ABCD的位置，即位置5；执行到第7步时，虽然ABCDE之前都出现过，但由于数据字典中记录的是第二个ABCD的位置，因此，重复串为ABCD，而不是理想的ABCDE。Zippy的这种实现方式牺牲了压缩比，但是提升了性能。

2）Zippy内部将数据划分为一个一个长度为32KB的数据块，每个数据块分别压缩，多个数据块之间没有联系，因此，只需要两个字节（确切地说，15个位）就可以表示匹配串的相对位置。另外，Zippy内部还对匹配信息的表示进行了精心的设计，采用变长的表示方法。如果匹配长度小于12个字节（由于前面4个字节总是相同，所以4＜=匹配长度＜12，可以通过3个位来表示）且匹配位置小于2048，则使用两个字节表示；否则，使用更多的字节表示。总而言之，Zippy对匹配信息的编码和实现都非常精妙，感兴趣的读者可以阅读开源的Snappy项目的源代码。

相比Zippy,BMDiff算法实现显得更为激进。BMDiff算法将待压缩数据拆分为长度为b（默认情况下b=32）的小段0……b-1，b……2b-1，2b……3b-1，以此类推。BMDiff的字典中保存了每个小段的哈希值，因此，长度为N的字符串需要的哈希表大小为N/b。与Zippy算法不同的是，BMDiff算法并没有保存每个长度为b的子串的哈希值，这种方式带来的问题是，某些重复长度超过b的子串可能无法被压缩。例如，待压缩字符串为EABCDABCD,b=4，字典中保存了EABC和DABC两个子串，虽然ABCD重复出现了两次，但无法被压缩。然而，可以证明，只要重复长度超过2b-1，那么一定能够在字典中找到。假如待压缩字符串还是EABCDABCD,b=2，那么字典中保存了EA、BC、DA、BC，压缩程序处理第二个BC的时候，发现之前BC已经出现过，因此，往前往后找到最长的匹配串，即ABCD，并输出相应的匹配信息。BMDiff适合压缩重复度很高的速度，例如网页，Google的Bigtable系统中实现了列存储，相同列的数据存放到一起，重复度很高。