第9章 50%的羊毛

我认为某些公开发表的解说，远比现象本身更值得注意。

——史密斯（High M.Smith）

本章目的 对许多工业界人士而言，商业交易行为中，没有比使用“操作定义”（operational definition）更重要的了。本章旨在向读者引荐操作定义的需要，激发读者进一步探讨。

也可以这样说，在工业界的需求中没有一项比“操作定义”更为人所忽视。我们在大学人文学院的哲学及知识论课程中学到操作定义，但却很少在理工学院或商学院学到。甚至可以说，物理、化学及其他自然科学的学习中，并不讲授科学的哲学。

“意义”始于“概念”，它存在人心之中，无法言传。任何语言、处方、指示、规格、量测、属性、规则、法律、制度、布告等能够沟通意义的部分，都只是某些特定操作或测试运作的记录而已。

什么是“操作定义”

操作定义可以把可沟通的意义化为概念。但是良好、可靠、均匀、一致、完美、疲劳、安全、不安全、失业等形容词并没有可沟通的意义，只有当它们应用在抽样、测试及准则时，才能表达。定义的概念是无法言传的，也就无法传达给别人。而“操作型”定义则是每个有理性的人都能一致认同的。

我们可用“操作定义”来做事。诸如“安全”、“完美”、“可靠”或其他质量的操作定义都必须是可以沟通的，对买卖双方都是同样的意义。对制造业工人而言，过去及现在的意义都同样。如：

1.对材料或装配线所做的特定测试

2.用来判断的准则

3.决定（同意与否？物件或材料是否符合规格？）

一件东西的规格，指的可能是长度、直径、重量、硬度、浓度、羊毛状（flocculence）、颜色、外观、压力、平行度、渗漏与否、失业率或其他特性测定值。规格也可能指的是“性能”，例如某机器的平均故障间隔就必须不能少于8小时，或者是买人的机器必须最少要有95%能运转无误达1小时以上。

我们可以在许多地方都能了解，买卖双方相互了解有何等重要。双方必须要使用相同的测量单位，仪器也必须相互一致，而且只有仪器处于统计控制状态下，规格才有意义；没有操作定义，规格就毫无意义可言。

公司及部门之间，彼此对原料合格与否或仪器功能正常与否引起误解，因为他们未能事先用意思清楚的术语说明产品或性能规格，又未能了解量测问题。

操作定义对于律师非常重要，对于政府法规非常重要，对于工业标准也无比重要。譬如说，什么是“注意”（care）？什么是制造时“适当的注意（due care）”？（参见第17章的原则4）

“实践”远比“纯科学”确切，也比“科学”来得确切 正如休哈特所言，产业界及公共服务所要求的知识及技艺标准，都比纯科学所要求的还来得严格。

纯科学及应用科学两者对准确度反精密度的要求都愈来愈严格了。

可是应用科学（特别是可互换零件的大量生产）对准确度及精密度的要求，在某些领域上，甚至远比纯科学确切。例如，某位纯科学家做了一系列的测量，并据以做出他所认为的准确及精密的最佳估计，没有考虑到他手头的测量值其实很少。他大可轻松承认：

未来的研究或许会证明这样的估计值有误。也许，他对该组数据只能宣称：这些估计值与其他科学家在当时现有资料下所做的合理推测不相上下，但是应用科学家则不然。他知道如果根据纯科学家当时手头的贫乏证据而行动，他可能会和纯科学家一样犯同样的错误。他也知道，这些错误可能会使人大亏老本，或受伤，或既亏老本又受伤。

此外，产业界的人士还有另一层忧虑。他知道质量规格所包括的“一定程度”的准确度及精密度，也许会纳入合约中，因此规格所用的名词定义如不确定（包括准确度及精密度），都会导致误解或法律诉讼。所以应用科学家都会为了这些名词尽可能合理地建立确切可行的意义。

没有精确值，也没有真值 商业方面的问题从不涉及精确的圆（百分之百），而是与真圆相差多少。汽车上的活塞就不是精确的圆，它也“不可能是”，因为我们无法在操作上定义出精确的圆来。

此时，何不求助于字典呢？字典上说，假如欧几里得二维空间上的某些点都与圆心等距，则称该图为圆形。此定义在正式逻辑（例如欧氏几何定理）运用上，相当好用。但如果我们试图把它应用在实践上，就会发现，字典提供的只是一个“概念”，不是适用于工业的定义——换言之，它并不适用于特定目的——“圆”的操作定义。

火车不会确切准时。

为了要了解这些真理，只需设法解释“做什么量测”、“采用什么准则”来决定某物是否精确的圆，或者火车是否确切准时？我们就会很快发现自己陷入进退维谷的困境。

任何物理量测都是应用既定程序的结果。计算地区人口也是这样，我们可以预期依两种不同的测量或点估计程序（称为A与B）所做出的量测，会得出不同的结果。这两个结果无所谓对错。但该行业的专家也许会有所偏爱。布列吉曼（P.W.Bridgman）先生这么说：“概念其实就是与对应操作的集合。”用下面这段话来解释，也许更容易懂：

所谓受偏好的程度，其特征是：它的产出结果最接近特定目的，或者它本身就是较贵或较费时，甚至不可能实现……因为受偏爱的程序总是要常常修正或舍弃，所以我们只好这么说：任何程序的准确或偏差与否，都无法以逻辑来了解。

我们早就知道，生产过程平均会随着抽样方法批次的使用以及测试方法与判定准则的不同而不同。只要抽样或测试方法改变，就会得到不同的不合格品数目及不同的生产过程平均值。因此，某一特定批次内的不合格品数目，没有所谓的真值，生产过程平均也没有真值。

大多数人也会惊讶于光速是没有真值的。光速是依实践者所使用的方法（微波法、干涉器法、测地学法或分子谱仪法）而得出的结果。就像前面强调的一样，除非量测方法显示结果是在统计控制之下，否则该方法不算好方法。惟一用统计控制测出的却未在统计控制状态中。

如果两个测量光速（或任何东西）的方法都处于统计控制状态下，它们在科学上的重要性仍可能大不相同。反之，假如两个结果相当一致，其一致性就可视为今日所能接受的主标准。

主标准不一定就等于真值，因为还有其他尚待验证（但和现在主标准不同）的值。最好把这种尚待解决的差异，视为不同方法所产生的当然结果，而不是偏差。

我们在学校所学的3x10¹⁰（厘米/秒）光速值，在大多数场合还是适用的，但是今日的科技和产业却要求其他更精密的方法（精确到小数点以下7~8位）。休哈特博士早在他1939年的著作中（该书89页），就将当时各种书上所发表的光速值画成图表记录（图9.1）。图中显示出愈到后来测量值愈小。最近的许多光速值也都比以前来得小，只有一次例外（系由前苏联所发表）。

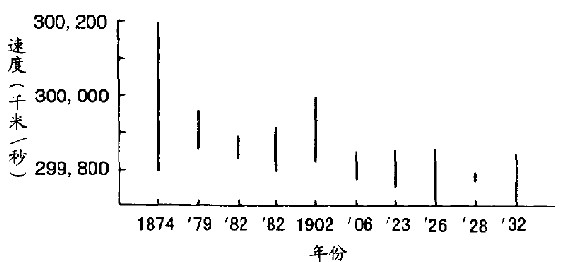
图9.1至1932年为止，人们所发表出的光速测定值

垂直线段部分代表光速的可能数值范围，计算方式通常未明示。

以美国人口普查为例 人口普查中也没有真正的居民数目真值。美国人口普查局官员甚至会忽视某些科学上的基本原理。我听过一位人口普查局官员说：“1980年的普查是有史以来最为准确的一次”。我怕这种说法会导致他自己和其他人误以为有所谓的“准确值”存在，而且只要全体人员努力就可达到。

有许多市长抱怨1980年4月的普查，未能涵盖该市的所有人口。很遗憾地，这显示出市长们不懂得什么是人口普查。而法院想用法律力量来调整普查值的不合格做法，也显示其对人口普查无知。何不干脆在每地区多给2.5%的经费呢？（译注：美国各地依人口普查值，拨放各种补助款。）

底特律的市民数目真值是什么？我们永远不清楚，但依人口普查局的程序，还是可以得出一个数值的。只要程序有所不同，结果就会跟着不同。

我认为有种合理的方法可使市长对该市的人口普查满意。要这么做，先要和普查局合作。该市长要做的是：

1.研究并熟悉美国及其他地区的人口普查方法。包括哪些人要计入，定义哪些人可不计入，以及如何将某人从某区归属至另一区。

某地区空住宅单元的计数，既会发生分类问题，又会影响总数计算。什么是“住宅单位”？什么是“空住宅单位”？这类问题看来简单，但是只要探讨过各种住宅单元后，就知其不然了。表面上，无人居住的住宅单元就可算是空的。但是，要是房屋不适人居住呢？它们是否也算空的？有些空房待售，有些则待租；有的只是季节性使用（一年只住几天）；有些空房既不租也不售；有些即将有人迁入。

空住宅单元的类别和数目是重要的经济指标，是具商业价值的。显然，普查局在派普查人员实地点算前，一定要让他们先接受训练。

2.要了解这些程序，最好是申请参加普查局举办的四日研讨会及参加考试。

任何熟悉人口普查的人，都知道普查局想在4月8日夜间，努力寻找并计算出简易住所、监狱及居无定所者的各行各业总人数。这些人之中许多人对自己一无所知，有人不知道自己的名字，更多人不知道自己的年龄。一大批计数人员及其他普查人员都加入此一搜索网，监督严密并经排练。

值得注意的是，在合理的范围外，想花更多的努力及费用去找出精确人数，就会白费功夫——特别是18~24岁的男性黑人。要想以密集搜寻的方式多找出一个人来，很容易就会再多花100美元。如果还想更进一步了解，则要再多花200美元（每人）。

究竟花费要到何种程度才适可而止呢？

所谓的“某地区人口数”究竟是指什么呢？

显然，我们必须事先同意要花多少功夫以及谁要多付额外费用来加强求证。

3.了解各国人口统计估计的技巧。如（a）住宅单元及失踪的人数；（b）重复计算的人数；（c）点估计的误差。

顺便一提，有一堆名册上并未出现过的人宣称，他们没必要被登记在上面。其实不一定非得在家不可。只要看看普查局的记录，就可以了解某人是否已计入，并将其归入住家。

4.对各种程序不断地提提高建议，直至令人满意为止。

5.（a）针对选出的小范围地区，监视其普查行动，以提供真实发生的统计证据。

样本中的区域可依地图选出，约含有10~50个住宅单位（没有严格限制）的任何地区，最重要的是该区域必须有清楚而毫无差错的界限。

（b）除非监视结果显示“执行失败”，否则就得接受人口普查局的结果。“执行失败”的定义也必须事先界定。

要是市长没有参与，就得接受调查局的数字。如果喜欢事后抱怨，不就像在玩“正面我赢，反面就重来”的丢铜板游戏吗？大概谁都不想和人玩这样的游戏吧！然而，市长们正是要其他人这样做。

法官及其同事要想够格审查控告人口短估的案件，就必须先参加人口普查方法的短期训练，并了解“概念”与“操作定义”的基本差异（本章内容可列为法学、工程、商学及统计学的训练教材）。

操作定义的进一步探讨

每一个人都自以为了解“污染”的意义，直到想向别人解释，他才领悟到自己并不明白。我们需要河流污染、土地污染及街道污染的操作定义。因为除非能以统计方式来界定，否则这些名词毫无意义。譬如说，光说“空气中有100个PPM的一氧化碳是危险的”仍不够充分，我们必须先详细规定：（a）在“任何时刻”一氧化碳含量超过100个PPM就会有危险；（b）在“工作时间”内，如果空气中一氧化碳的数目超过100个PPM就会有危险。

再者，一氧化碳的浓度如何量测呢？

污染的意义（例如）是否是指一氧化碳的浓度高到足以使人呼吸3次就会致命，或是指一氧化碳的浓度高到连续呼吸了5天就会致病？不管是哪一种情况，如何确认一氧化碳的影响呢？要用什么程度来量测一氧化碳呢？中毒的诊断准则是什么？对人的标准是什么？对动物的标准又是什么？如果用人，我们如何挑选样本？人数多少？样本中的人数要多少才能符合一氧化碳中毒的准则，然后才能宣称多吸几口不安全，或仍可习以为常？如果使用动物，我们也要问同样的问题。

对工商业而言，连“红色”这个形容词都没有意义，除非能用“测试”及“判断准则”来找出操作定义。以“洁净”为例，餐厅中对刀叉及碗盘的“洁净”要求，就和电脑硬盘制造商及电晶体制造商所要求的不同。

商业或政府人士，对于产品或药品或人力、性能的规格了解，不能只停留在表面。在纯科学的领域里，知识理论的原则常被视为是不重要或过时的玩意儿，与经营管理有关的教科书也这样认为。但是，在面对工业问题的人而言，这却是很严肃而迫切的。

美国法律规定市售奶油中，必须含有80%的脂肪，其意义究竟是什么？是否表示每镑奶油中至少要有80%的脂肪？或是“平均”为80%？如果平均是80%，意义又是什么？是指一年内你所购奶油的平均值？或是指你和别人每年从某一来源所买的各种奶油的平均值。你会拿多少磅来测试？试验奶油如何选用？你会在乎每磅奶油脂肪间的不同变异吗？显然，想以操作定义来界定80%脂肪就必须借助统计技术及准则，只提“80%脂肪”并无意义。

就效益及可靠度而言，“操作定义”也是必要的。诸如失业、污染、货物及仪器的安全标准、有效性（如药物）、副作用、副作用发生前的药效时间等，操作定义要是不用统计名词来界定，这些概念都是没有意义的，问题的调查或研究就会变得既昂贵又无效，而且几乎一定会造成永无休止的争辩。

以鼻子过敏来定出污染的操作定义就是一个例子，这并不是不可能（与维护食品及饮料的质量及风味类似），除非用统计方法加以界定，否则它就毫无意义。

测试样本的数目如何选择和估算，不确定性如何计算并解释，检验仪器之间、操作员之间、日期之间、实验室之间的变异，以及检测并评估非抽样误差的影响等都是很重要的统计课题。两种调查方法（例如问卷与测试）之间的差异，也只有靠统计设计及计算才能可靠而经济地加以衡量。

国会所通过的法律及联邦主管机关订出的法规，都是定义不清、混淆误事的例子。下面一小段话引自《纽约时报》1980年4月9日D-1、D-3版，它说明了联邦通讯委员会（Federal Communications Commission）终于放弃想区别“资料处理”与“数据传送及处理”一事。

资料处理（处理文字及数字形式的资料）与电信（声音的传输素为电话公司的主要业务）之间的区别即将消失了。

许多观察家认为，这就是迫使该委员会介入业界所谓“第二阶段电脑查询”（Computer Inquiry II）的最后据点。

过去十多年来，联邦委员会一直想解决什么是“资料处理”及“电信通讯”的基本问题。就在这同时，这两项科技都突飞猛进，超出了法规所能管制的界限……

“每次委员会愈想分开这两个区域，它们反而愈紧密，”某电信产业观察家如是说：“现在委员会借着开放资料处理业的业务给电信业者，实际上就是在推动它。”

“50%的羊毛”表示什么？ 毛毯上标示为“50%羊毛”的标签是什么意思？也许你并不怎么关心标签上的成分标示，反而对颜色、质感及价钱更有兴趣。但是有人真的很在意，包括美国联邦贸易委员会（Federal Trade Commission），该标签的“操作定义”是什么呢？

假如你告诉我，你想买一条50%羊毛的毯子，我就会卖给你如图9.2所示的毯子——上半部纯棉，下半部纯羊毛。就某定义而言，这是条有50%羊毛的毯子没错。但是你的目的也许让你偏好另一种定义，而表示这不是你所要的。那么，你要什么呢？你要的是羊毛均匀分布的毯子。你的操作定义可能如下：

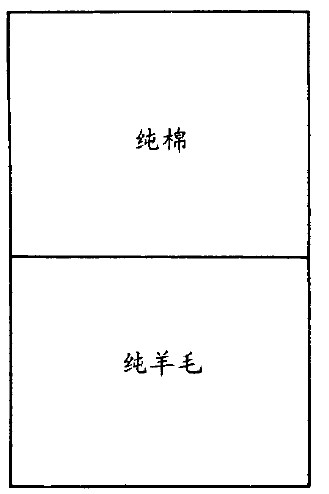
图9.2 50%的羊毛毯子（依区域分）

随机从毛毯上选出10点，割下10个直径约为lcm（或1.5cm）的毛毯。将其依序编号为1~10，交给化学师化验，让他按规定测试。并要求他记下i样本所含的羊毛重量比率（xi），并说出10个样本的总平均值（）。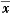

准则：

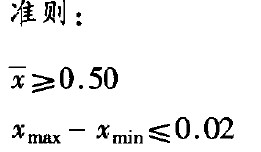
如果样本不合乎上述任一准则，该羊毛毯就未能符合你的规格。

上述两种“50%羊毛”的定义没有所谓对错。你有权利也有责任依你的要求定出一个定义，将来目的不同了，也许又会有一个新的定义。

毛毯中羊毛成分的真值也不存在。可是我们却可用指定方法得到一个数字。

前面我们讨论的只是一条毛毯而已。现在可要讨论许多条毛毯了。如果我们为医院或军队买毛毯，就会碰到与一条毛毯不同的根本差异——单次采购与连续采购（参见第2章）。你可以规定制造商在每10公斤干净的羊毛里加入10公斤棉花。这可能就是“50%羊毛”的定义，无所谓对或不对，只要符合你的目的即可。

另一个应用的例子。《美国新闻与世界报道》在1981年11月23日第82页报道如下：

你能做什么，不能做什么

美国某地区法院同意：如果你是一位靠外国制造厂供应标签的进口商，只要该标签标示不正确，就会被判违法。纽约地区的一家进口商，在联邦贸易委员会通知他织品的羊毛成分与标签不合后，仍照卖不误，最后课以2.5万美元罚金。根据裁决，该公司必须委托公正的实验室来决定标签成分是否属实。

如果要为“25%羊毛”定出定义，原告和被告不知会怎么协议。

什么是“皱纹”？

本产品为汽车仪表板。某一样式的仪表板毛病特别多，该厂厂长告诉我，他们的不合格率一直都处于35%~50%之间。

检视过资料后，我发现检验员之间差异极大。原来每位检验员都有一套自己的“皱纹”标准。该厂经理主管同意花些时间来讨论操作定义，6位高层主管出席了该会议。检验员拿出20块仪表板，其中有些有皱纹，有些没有。

我先要求在场每一个人界定“皱纹”的定义，定义要让人人都能懂。但是出席者一点反应都没有。我再问一次：“哪一位检验员能告诉我‘皱纹’是什么？”仍旧没有答复。接下来质管经理指给我看，他所说的皱纹是什么。一位检验员同意那是“真正的”皱纹。然而其他4位检验员中有两位却说：“到底要找什么呀？”他们根本看不出有皱纹。

解决方法是先建立皱纹的操作定义，判定何者为皱纹，何者不是，然后再建立起其他缺陷的定义。

结果：该厂在一周之内不合格率的水准就降为10%。负责重修的工人终于有时间去做他们该做的事了。操作定义在检验员与操作员之间，提供了一个沟通的基础。他们不但可以拿来自我训练，也可以互相训练。产量因而增加了50%。

公司不花一文钱，依然是同样的人、同样的原料、同样的机械。惟一的新鲜事只是增添了定义而已——能为现场及检验人员共同了解。

随机选择的单位 从N单位的群体中，抽取样本的随机程序，可界定为：

1.该范围内的单位分别编号为1、2……到N。

2.由一事先同意并写成书面文字的程序中，大声读出从1到N个不重复的随机数。读出的数字代表了样本序号。

这是个随机程序的操作定义。它的样本既不是随机的，也不是非随机的，但我们的重点在于选样的程序。此选样程序必须满足随机程序的规定定义，否则它就不是随机程序。而随机数则是随机操作的结果。

我们可使用标准的随机数表，或在数学家指导下自行产生随机数。（以避免随机数产生过程中可能发生的谬误）（请进一步参见第11章241页）

练习、答案、评论

1.为什么我们可能找不到任何事物“真值”的操作定义？

答案：任何事物的观察数值皆视其定义及操作方法而定，不同专家的定义和操作方法都不相同。

2.（a）请说明为什么系统的测量必须是在统计控制状态下才够资格称为测量系统。请详细探讨同一物品的重复测量值、交换测量员后的结果，并在下个月再重复测定。

（b）说明为什么任何测量系统的准确度只能和“一个可接受的测量全标准的平均值的离差”来界定。

（c）如果主标准改变，该测量系统的准确度也会跟着改变，可是测量系统的精密度并不受主标准影响。

（d）当你在决定是否依主标准调整测量系统时，须考虑哪些工程及经济方面的因素？

3.请说明为什么测量的准确度只能用和“一个可接受的主标准测量结果的离差”来界定。

答案：准确度会随标准的改变而改变。

4.你如何回答某城市某自行车生产商所提出的问题。

美国政府曾有如下法律规定：由中等智力人员所装配的自行车，必定安全无虞。

这法规的意义是什么？你如何向他解释？什么是安全？什么是不安全？什么是中等智力的人员？什么是智力？是否智力较差的人工作的质量反较好呢？如何界定智力较差？我们只能说该法规并无意义。

评论：工业界自己发展出标准（见第10章），可以避免此种无意义而又令人困扰的法规出现。

5.（a）请说明为什么除非测量系统及其所用的标准都在管制状态之下，否则该测量系统就没有可证实的精密度及可证实的准确度（和标准比较）可言。

（b）分析化合物中的三溴甲烷（bromoform），其结果为86.5±1.4[10^-9毫微/微升]。美国国家标准局并用±1.4这个范围作为95%的置信。试说明此区间（±1.4）有何操作意义。在何种情况下，我们可用以预测6个月后，同一化验室测试结果的全部？

（c）你能否定出计划来显示测量系统是在管制状态下？

（d）测量系统是否包括该检验材料的抽样？它是否包括了样本间的变异数？

6.试说明为什么商业上要了解并使用经济及人口资料（当然包括行销研究）时要用有调查经验的人较好。

7.试说明为什么在实验或调查时如果结果的“精密度”那时有效则将永远有效。结果的“准确度”却时时随新定义或新方法的改变而改变。

8.铸造物的规格中，包括有下述条文：

铸品交货时必须保持适度清洁。

什么是“适度清洁”？此规格指的是产品必须闪闪发光或只是略有污物？显然，此规格如果要想有意义，就要订出“适度清洁”一词的操作定义。

9.试指出下一段文字中内容并无意义：

国会已通过法案，授权美国东北走廊的重建，甚至规定火车速度必须为每小时120英里，要有99%的准点率，从纽约到华盛顿的行车时间须为2小时40分，而纽约到波士顿的支线行车时间则应为3小时40分。（1976年，《大西洋月刊》，36页）

评论：很显然，准点率的定义，必须要有操作定义才会有意义（参见第17章）。

诸如“服务良好”、“服务不佳”、“服务令人可叹”等形容词，在沟通上不具意义，除非用“到站记录图的特性”或“到站分布的特性”等这样的统计名词予以界定。

我们很容易看出，国会所期望的99%准点率，除非已有“准”时的操作定义，否则就没有意义。如果所谓的“准时”是指与印出的时刻表相差4小时以内，那么任何人都可保证100天中有99天火车会准时到站。

在生产时间安排上也同样适用。

10.请说明下列两例（从工业界及政府所用的规格中摘述），没有可沟通的意义可言：

（a）代表性样本（representative sample）。“‘代表性样本’与所抽样的材料具有相同的成分，如果我们认为母体是均一的。”（英国国家标准69/61888“化学产品的抽样方法”。）

你如何决定样本和被抽样的材料成分是否相同？请解释为什么“与被抽样的材料具有相同成分”没有意义。

（b）现场样本（spot sample）。“从材料的特定地点或从产品流程特定地点或时间内，所抽出特定大小或数目的样本代表当时或附近的环境。”

“代表性”这个形容词的意义是什么？

答案：这词没有意义。统计学家不用这个字眼。为什么不干脆使用有统计理论作基础的抽样程序？其成本较低，又可以取得有意义及可计算的公差。

11.最大努力：“订约者必须尽其最大的努力。”（摘自美国司法部税务处与某统计学家所订的合约。）

谁知道“最大的努力”是什么？你如何断定他已“竭尽所能”？他是否每件承诺都能全力以赴？会有任何努力落在平均水准以下吗？

12.下文引自某一著名《实验设计》的教科书，因为其中“精确值”（exact value）一词没有意义，所以容易使人误解：

显然，我们不能期望该解法能提供未知差异的精确值。（科汉（William G.Cochran）及考克斯（Gertrude M.Cox）合著《实验设计》（Experimental Design，Wiley，1950版），第3页。）

13.什么是“教育面前人人平等”（equal education for everybody）的意义？