第13章 随机中奖

这目标令人钦佩，但方法却有些疯狂。

——《华尔街日报》

每一个问题都有一个解决办法：简单、利落及“错误”。

——《商业周刊》

本章目的 在本章，通过列举现实生活中5个例子分析了它们失败的原因，并强调解决其中的问题需要借助现有的资讯。

所用的基本原则

以下案例之所以失败，乃是由于未能了解下列4个通则所引起的：

1.一群点中间，有若干点一定在平均值之上。

2.非所有点都在平均之上（只有极少数巧合例外）。

3.质量及数量的统计控制变异，确实有一理想状况存在，但其上下变动均须符合“随机”的准则。换句话说，“变异”必须是稳定的。在统计控制下的质量特性是稳定、恒常的，此一特性每小时必然会重复显现（第11章）。如何使变异缩减及达到更稳定的水准几乎全为管理阶层之责。

4.变异及损失不仅来自“特殊原因”，也来自系统本身所引起的“共同原因”——如果有“系统”存在（第11章）。

前两条通则或许会让读者以为我在试写连环图画。不是，这个可悲的事实是：美国的行政及管理实务都忽略了这4条通则。

例1 总是有人在平均之上。在某一专业场合，某公司董事长想向我展示他的资料处理设备，此一设施需要60位女士把卡片打孔。我问他打卡错误率是多少，让我很惊讶，他竟然知道。他比大多数人都先进。因为许多管理人都说自己没有错误，他们的职位也不允许他们犯错。他告诉我说，平均错误率是100张卡片里有3个错误。他每周三会收到一份汇总的证明报告，显示出每一位女士前一周所犯的错。

他因此想出一个管理上的绝妙创意：找那些上周犯错超过平均值的女士来谈话。

我问：“那么，这就是说，你每周要和30位左右的女士谈话了？一周接着一周。”

“是的，”他回答，“差不多就是这个数字。你怎么知道？”

我于是告诉他最近伦敦《泰晤士报》的一封读者来信。该读者研究了健康部的一篇报告之后发现，英国显然有一半儿童的体重低于平均值。这真是国家耻辱，必须提高孩子们的营养。

我的听众闻言大笑，但他并未深入了解，自己的管理方式也会落入同样的陷阱，甚至只会造成更多错误，而不是更少。

在不自觉的情况下，他陷入每周都要从60位女士中随机选人来谈的危险。其实用一些简单的统计技巧就能告诉他哪些女士需要协助（如接受较佳的训练，或转换到其他工作去）。

我问他：“你的努力达到了多少效果？”回答可想而知：他很失望，一点提高都没有。更糟的是，不管他知道与否，他的努力只会让挫折及困扰愈来愈多。

例2 最终产品是精炼糖。它的原料大部分是粗糖及海水。因为工厂位于海湾旁，并无适于制糖的新鲜淡水可供应，因而主要考虑的是“水”的成本，工厂必须从海水中除去盐分及其他化学物质制造淡水。

目标：让每吨最终产品减少至3.5吨的海水使用量。

方法（错误的）：调查用水比例高于3.5吨时的情况。

我问：“3.5这个数字是从哪里来的？”

“我们开了一次会议，决定我们可以达到这个标准。”

当我应邀到该工厂访问时，我看到布告栏上挂着一列色板，有些是绿色的，有些是红色的，每一块色板都代表了当月的某一天。绿色色板表示海水和精炼糖的比例低于3.5，红色色板表示恰好相反，如此一来生产线的人员就会得知前一天的比例是多少：红色色板出现，大家就会聚在一起，试图找出前一天有哪些操作错误。结果，他们自然会提出各种解释，尝试采取矫正措施——这样做都是错的。如果第二天变成绿色色板，他们就会喜滋滋地认为自己已经找出了浪费之源，非常满意红色板在整列中，仅出现一两天或两三天。

“精制一吨糖需用3.5吨水”是一个数值目标，这个目标虽然经过所有参与同仁的同意，然而仍只是一个没有计划的数字目标而已，只能在目标未能达到时，试图找出原因所在。此种计划暴露出在第11章例1中所看到的同样错误。也会导致由于过度调整（第11章217页所示的第一种错误）或调整不足（第二种错误）所产生的不必要的严重损失，导致提高之路满布荆棘——困难、危难与迷惑，当然绝非最佳营运状况。

较好的计划是通过小组研究生产过程，试图应用化学知识为辅，再依据第2章休哈特循环（图2.3），细心地使用良好的实验设计。

根据每一吨糖每日所需用水的情况所做出的控制图，可以显示出特殊原因（如果有的话），并可作为提高记录。

我要强调，为了了解及提高生产过程起见，所做的实验及资料搜集并不是必要的。温度当然随时会变，没有事物是恒常不变的。根椐不同的方法、生产过程及混合状况，当然可以做出一系列温度的连续记录，可以有“压力”的连续记录及有“速度”的连续记录。不定期的记录便可以达到此一目的。观察高低温度、高低压力等对产量、产品测量值的影响，并通过工程知识判断，便可找出生产过程提高的线索。比起那种从头便须表达出实验目的的及改变温度、压力、速度的实验计划，这个方法也可能便宜而较佳。东京的朋友西堀荣三郎博士向我提及，观察自然变异的一种经济而有效的方法是“简单观察法”，简单观察法不能解决时才采用“实验”。朋友哈掩克博士（Hugh Hamaker）在荷兰的飞利浦公司任职多年，也曾强调同样的主题。

换言之，本书许多地方所强调的便是善用现有的资讯去解决问题。

例3 当我前往参加某一客户的会议时，行车途中，车子发生故障，要更换一条新的风扇皮带。在修车厂等候时，我看到墙上的布告：

我问该厂主任：“什么是顾客的最大满意？”

主任回答说：“顾客抱怨数最少，当月退货数最少。”

接下来便是我们之间的问答：

问：某些机械员是否有“零抱怨”的记录？

答：经常如此。

问：那么，每月每人平均抱怨数为多少？你是不是都做了记录？

答：没有，但我很清楚平均数。我不时运用一些判断。例如新的汽化器因不易调整，所以我不把对它的抱怨列入计算。

问：是否所有的技工逐月下来都是大约相同的平均数？

答：是的，的确如此。当然有时会有变化，但最后他们都会达到差不多的水准。（我应该问他：你怎么知道？）

问：是否有任何机械员的名字永不上榜？

答：不是永不上榜，是轮流上榜。

问：如果某月份有两人的分数相同，你如何处理？

答•.我会同时公布两人的名字。

问：你如何知道两人不分胜负，除非你有记录？

答：我很了解我属下的表现。

问：是否有某一技工连续一两年内，名字老是出现在墙上？

答：没有，大家总是在轮换。

问：是否有人连续两个月是零抱怨？

答：是的，有这种事。

问：你认为这种考绩制度是否有效？

答：前几年颇有效，但现在已不那么令人兴奋了。

我原先以为主任会问我为什么对这件事这么有兴趣，但他却没问。从他的回答看来，我的结论是，这种荣誉制度和抽奖一样。他的回答完全符合随机模式。这些数字已经够格用作随机检验了。让我们看看一些随机性的含义（统计控制的状态）。

就每人每月总平均数为两件抱怨而言，一位维修员在当月没有抱怨的机会有e^-2=1/7.4（假设抱怨是独立事件）。若每人每月的总平均有3件抱怨，则他在当月中没有抱怨的机会为e^-3=1/20。这些概率显示出，如果某人达到统计控制状态时，现在既然每月平均有一两件抱怨数，他只要耐心等待，便可上荣誉榜。实际上，他很可能发现自己连续两个月上榜。他如果当月上榜，下个月就很可能也上榜。反之，也许就要等待一段相当长的时间了，只能靠机会。

总之，看来我们似乎有一套可以提高服务质量的系统。而实际上，假设人们再也不关心它，它就会毫无成就。假设人们关心，并想得到此项荣誉，它根本就是在打击士气及服务质量。

士气再诠释

一位纽约大学的学生听完我对上述主题的演讲之后，送给我一段下述摘自基根（John Keegan）所著《战役的面目》（The Face of Battle，Viking，1977）一书的文句，表明他的决心：“从现在起，我将用不同的眼光来看伟大的将军。”

讲到伟大将军的影响力及天才有下面这样的一则故事。

费密（Enrico Fermi）曾向葛洛夫（Leslie Groves）将军问道：有多少将军可以称之为“伟大”？葛洛夫说：大约百人中有3人。费密接着问：称之为“伟大”的条件是什么？葛洛夫回答说，只要任何一位将军连续赢得5次战役，就可称之为伟大。

此时正在二次世界大战中期。费密说：这样一来大多数战场的对抗势力既然大致相等，我们就很可能在两场战役中找到一位将军会赢得一场，有1/4的机会他会连续赢两场，有1/8的机会他会连续赢3场，有1/16的机会他会连续赢4场，有1/32的机会可以连续赢5场。到了最后，他说：“将军，你是对的，大约有3%的机会，这只是概率而已，并非天才。”

例4 我们常常在商业报道上读到有关大制造厂打算以计划成功与否来选用广告商的事：如果某产品或某系列产品的销售量连续两年下降，公司便会考虑更换现有广告商。

现在，任何人想以不适用的统计技巧来衡量广告效果，都会痛苦地发现，实际上有很多股势力会使销售量或市场占有率降低。广告（或失败的广告）都可归诸于这样的“一股力量”，但在众多可能原因之下，它很可能只是广告商的坏运气而已，成功与否全属猜测。用以形容这样的系统最适当的是“摸彩”，广告商只能碰机会：他可能贏，也可能输。

假如有人因想出上述的衡量法而升迁。同事或许会误认为他的升迁是因为此举成功而来，他本人当然也这么想。

例5 成本效益分析的谬论。成本效益分析的公式为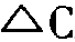/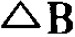，式中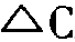为计划中的额外成本（现有的或预测的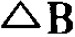），则为额外增加的收入。此种想法听来不错，容易理解，但却常常会碰到严重的困难。

1.“成本”有时是无从捉摸、很难估计的。例如，没有人知道到达顾客手中的瑕疵品会有什么样的成本（如电视显像管）。不满意一件低成本产品（如烤箱）的顾客，可能会对大量订单的决策造成影响，从而让其他制造商得到它。

2.“效益”的道理也是如此，有时甚至更难用金钱来衡量。可是，就交易的现点而言，各种利益是可以互相比较的，因此我们有时可以做出一张“效益等级”的表出来。

如果你不能满意地估计出分子或分母，你就不可能算出此一分数的数值，这也就是成本效益分析的问题。

我通常不用任何成本效益分析法作为产品设计的尝试，因为它可能造成伤害。