我陷在深淤泥中,没有立脚之地。
我到了深水中,大水漫过我身。
——《圣经•旧约》
本章目的 本章将总结出一些原理。在各式各样可能实际碰到的情况中,这些原理会告诉我们,怎样才能使进料检验的平均总成本最小化,以及如何使修理及重新测试的成本最小化(因不合格品生产出来,却不能用)。
本章内容就算供应商和采购人员共同合作来降低不合格零件的比例,为了达到最佳经济效益,进料产品的使用仍需理论来指导。我们是否该试着从一大批进料中节选出全部不合格品呢?或是不管好坏,不加检验就全盘送上生产线?
本章由好几节组成。下节说明我们在什么情况下可以对进料采取“全数检验”或“全数不检验”的规则,以达到平均总成本最低的目标。在“其他实践情况”一节,则将“全检或全不检”规则延伸应用到生产过程不在良好管制下,但尚未达到混乱的项目。其次,讨论混乱状态下的处理方法(进料质量完全无法预测)。接下来是3个应用“全检或全不检”规则的例子。接下去是讨论最终成品无法修理,只能降级或报废的情况。下一节是多样零件的处理情况,再下来谈的是“标准接受计划”(standard acceptance plans)的处置,因为它们都适用于将平均总成本最小化的目标。
“量测及材料上的其他问题”一节,讨论额外的问题与环境,诸如采用成本比原测试法更低的方法,让一些瑕疵品进入生产线,造成产品些许报废,却不致使生产发生困扰。接下去是测量方法的检讨与比较。其中尤须特别说明的是,不管对委员会或管理阶层有多重要,“共识”在目测检验上却是致命的。“同意”可能只表示某检验员因“恐惧”或“不适当”而有所迁就。下一节的练习题则阐释“全检或全不检”规则的基本原理,同时强调“在好的统计控制状态下,样本和其余母体并无相关”。本章结尾,则再加探讨早先提及红珠实验的含意。
广泛应用的简单规则
假设 这里我们考虑“单一零件”的情况,然后再介绍“多样零件”的情况(见291页及308页的练习4)。
出厂前,每一成员都要测试。
如果进料质量有瑕疵,而且进入装配线中,装配出的产品就无法通过测试。如果进料零件并非不合格品,装配出来的产品就可通过测试。
供应商提供我们一批零件(称之为S),以取代我们发现的不合格品。
当然,供应商会把这些零件的成本记入账单内。此成本成为一般管理费用,但我们此处仅讨论变动成本。不管检验计划如何,反正这些费用都在那里,所以我们并不打算讨论一般管理费用的理论。
瑕疵零件是一看就知道会使装配品失效的东西。如果零件一开始就宣称自己有瑕疵,却不会在下阶段生产线造成麻烦或引起顾客的麻烦,那么这就表示我们对“瑕疵零件”尚未定义清楚。在这情形下的下一步骤,就是要检讨宣称某零件为瑕疵品或非瑕疵品的测试方法了。
当然,有些进料瑕疵要花很多的钱才能在工厂检查出来,所以只好留给顾客自己去发现(通常在几个月或几年后),这些通称为“潜在缺陷”(latent defects)。要解决这种问题的最好方法就是“改进生产过程”。这个问题另外还有一个解决办法——用破坏性检验来发现,但这样一来却会毁了该零件。
让我们假设:
p为进料零件批的平均不合格率(可能是一整天下来收到的材料)
q为1减去p
k1为检验一个零件的成本
k2为必须拆解、修理、重装配并测试的成本(因瑕疵零件进入生产线,造成装配品失效)
k在S件供应品中,逐次测试出相当数量的零件,以便找出良品的平均成本(本章练习7会指出k=k1/q)
k1/k2为平衡质量或平衡点(因k2永远大于k1,所以的数值会介于0至1之间)
读者可先阅读287〜289页的3个例子,然后再回过头来读下文。
全检或全不检 在某些情况下,最低平均总成本的规则其实非常简单。以下是状况1和状况2的说明:
状况1 即将进来的最坏质量的批不合格率小于k1/k2时,此时,完全不需检验。
状况2 进来的最好质量的批不合格率大于k1/k2,此时,全数(100%)检验。
要证明状况1和状况2的规则,更是简单(请参见下一节的练习4)。如把状况2当做状况1来处理,所引起的总成本将会极大化。反之,把状况1当做状况2处理,情形亦然。
“不检验”并不是叫我们在无知的状况下进行。我们必须确知,如果是状况1时,依过去之绩效而言,进厂最坏批(整周的进料)的不合格率,将落在平衡点的左方。状况2时,进厂的最好批的不合格率,则会落在平衡点的右方。买方及卖方手中所持有的控制图(最好是由双方共同合作做出),接下来会让进厂产品介于状况1或状况2,或介于两者之间。要是出现“混乱”的情形,也无法掩饰,因为大家都会知道。买方永远要照发票来检验进料确如所购(详见本章286页“永远不要没有资讯”一节)。
实践上所碰到的许多问题,状况1和状况2都可让它们达到平均总成本极小化,以下将出现更多的例子。
二项式跨步(binomial straddle) 假设生产过程处于统计控制状态内,而交货批中的不合格产品在平均值p附近呈二项分布。那么,要达到平均总成本最低的规则为:
状况1 若p<( k1/ k2)→完全不检验
状况2 若p>( k1/ k2)→全数检验
即使批中不合格品的不合格率分布,跨越在平衡点k1/ k2上。
所以说,统计控制状态有许多值得我们追求的显著优点。要了解这些连续进来的进料批是否处在状况1或状况2,或近乎混乱状态的边缘,我们只能时时注意统计控制的状态及其平均不合格率,或可定期采取小样本试验,画出的控制图来看——最好在供应商的合作下,到他的产业上去进行。
我们一定要注意,从批中抽取的样本和未抽取的母体剩余物品间在统计控制状态下是不相关的。换言之,在统计的管制状态下,样本不提供剩余母体产品的任何情报。(令人难以置信!但请参见305页练习1以及317~318页的图15.11~15.14)。
其他实务情况
其他稍离统计控制的跨步 我们现在要探讨进料批不合格率分布的其他两个简单跨步。我们可以根据控制图(由供应商或我方个别画出,或由双方协力完成),预测只有小部分分布会落在平衡点右方。就此情形,我们采取“不检验”的规则。只要该部分分布在平衡点右方的范围不要太大、不断开,而且尾端不要拖得太长,采用此规则就会接近“最小平均总成本”。
第二种情形恰与上述相反:进料批的不合格率分布只有一小部分落在平衡点的左方。有了这种知识,就可对进料批采取“全数检验”的规则。
图15.1显示我们所碰到的各种情形(包括即将要讨论的“混乱”在内)。
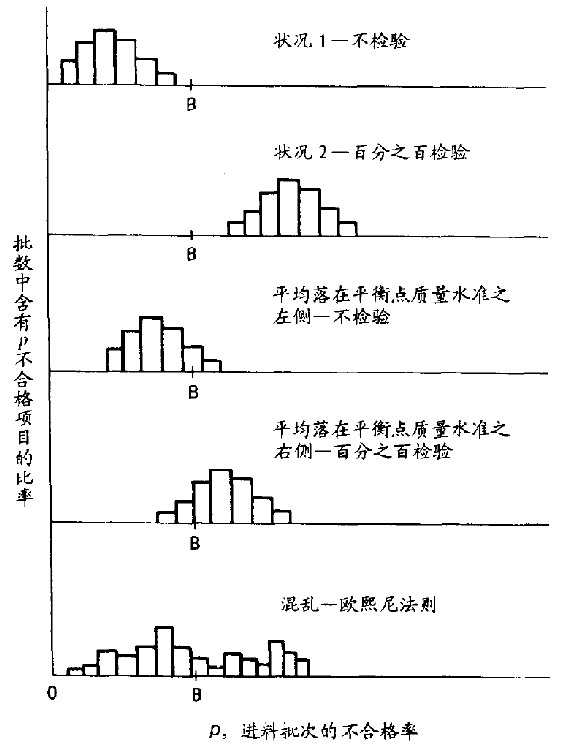
图15.1 进料项目的批状况
点B是平衡点质量水准,p= k1/ k2。
进料批的不合格率趋势 现在让我们假设趋势是向上的。今天我们在“状况1”中,完全不检验,但会随着时间而增加,趋势可能很稳定,也可能不规则。从现在起两天以后,我们将处于状况2中(我们事前得到了警告)。若进料批确实有某种趋势,则由供应商或贵厂所保管的控制图将会显示出来。很简单吧!
转换来源所造成的问题 我们从第2章中看过只改变进料来源在任何操作中造成的问题。我们以两个来源为例来讨论。如果两个来源都处于良好或尚可的管制状态,而且可以每隔数天,分别一次进货,原则上,我们就可分别采取状况1或状况2的对策(视其平均不合格率落在平衡点的左方或右方而定)。这种想法说来容易,但有些工厂却很难实施。
如果把两个来源的进料按一定比例充分混合,而且假定两个来源都显然处于良好的统计状态之下,那么从混合进料中取出来使用的批会呈二项分布,接下来我们就可以用“全检或全不检”规则求得新的最低平均成本。材料来自两个不同来源,会造成生产上的难题(我们已在第2章讨论过),两个从不同来源处充分混合后的材料产生的问题更令人头痛。
要解决此难题,第一步就是要把供应商减为一家(我们已说过一项物品、单一供应商的优点)。
如果供应商已减为一家,但送来的货物质量却不稳,那么他和他的顾客就必须共同合作,朝着状况1的方向来提高,最终达到“零缺陷”的目标。同时,我们接下来又会碰到“混乱”状态。
混乱状态 不合格率在平衡点附近左摇右摆地作小幅摆荡时,这种情形还算容易处理。当它离平衡点很近时,不论我们采取“全检”或“全不检”,都没有什么差异。要是我,我会采“全数检验”(100%检验),以便尽快地累积资讯。如果我们不敢预测进料的质量主要会在平衡点的哪一边,而且有时会在平衡点左右作大幅摆荡,那么我们已处于“混乱”状态。这种令人难以忍受的情况可能是来自于单来源送来的材料质量变化极大,且无法预测;或者是材料来自两个以上质量相差极大的来源(马鞍型的平衡质量,在平衡点两边摆来摆去),一个来源用一段时间,然后另一个来源用一段时间,没有一点规律或理由。此时我们当然应该尽快脱离此种状态,朝向状况1努力。同时,进料会继续进来,必须加以处理。我们又该怎么办呢?
如果现在进来每批货都附有标签,告诉我们该批材料的不合格率,那就没什么问题了。我们可依各批的标签,依它在平衡点的左边或右边,分别采用“全检”或“全不检”规则,达到最低平均总成本。
要是进来的材料未做标示,但处在“混乱”状态下,样本的质量和其对应剩余品之间却有相关,就可按混乱状态来测试样本,并决定是否把剩余物品送上生产线或加以筛选。采样或依某规则来使用样本,结果终有些批会误放在平衡点错误的一边,以致造成“总成本最大化”的不佳结果。
在混乱状态下,我们可采用100%的“全检”。实际上,这个决策值得考虑,但我们接下来要谈的欧熙尼(Joyce Orsini’s rules)规则也不失为好方法。
欧熙尼规则 在混乱状态下,欧熙尼规则是100%全检的另一简单代用法。它们易于管理,可以大大降低平均总成本(远低于100%全检的成本。我们把它拿来跟100%全检相比是有意义的,因为我们知道,全检的平均成本为: k1+kp每项目。法则如下:
当k2≥1000k1时,对进料批进行100%全检。
当1000 k1> k2≥10k1时,测试n=200个样本。若样本中未发现不合格品,接受该批。若本批中有一个不合格品,则筛选其余剩下的。
若k2<10 k1时,不检验。
样本数(n)等于200时,此样本足以作为进料产品质量的连续操作记录。好的连续记录形式,是依每个样本所碰到的不合格品数目作成控制图。此图最好合并几个样本,使样本中的不合格项目在平衡点上的次数平均约有3~4个。此连续记录图可让我们知道每日质量的变动情形,而此类信息有助于你及供应商辨认出他有哪一类问题。这些资料还会告诉你进料质量实际上是否混乱,或与预期相反(并不混乱)。此时我们可按状况1或状况2处理,损失极微。
下一周我们可以(甚至轻而易举)找出比欧熙尼规则更好的方法,看看过去进料的不合格率分布会告诉我们什么。但事实上,在混乱状态下,我们是无法预测特定分布的。如果我们知道进料批会有怎样的分布,就不会处在混乱状态下了。
我们还可以用另一种容易描述的程序来说明,如何在任何状况下让平均总成本最低,那就是安士孔伯(Francis J.Anscombe)的逐次计划(sequential plan)。安士孔伯建议,若前述的假说统统失败,我们仍应依序继续从批中抽取样本,其第一次样本的大小为:
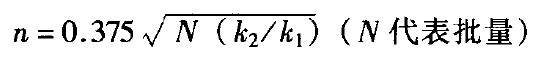
接下来,我们再抽取下一个样本(大小为n等于k2/ k1)继续抽样,“直到不合格品总数小于检验的样本数目减一”或全批都已检验。
不巧的是,安士孔伯规则并不是那么容易管理的。
上述的理论可用在顾客处修理或更换零件(只要我们知道成本)。惟一的障碍是,一旦产品到达顾客手中,就要用现金来支付修理和更换的费用(译注:即一般人只重视有形的失败成本),而它只不过是不合格品成本的一小部分而已。对你不满意的客户以后就不会跟你做生意了,而潜在客户知道了别人的不满之后,也可能使你遭受到巨大且难以估算的损失。
规则必须容易执行 规则要想实际应用,执行一定要简单。计算总成本时,必须考虑其执行的困难度,以及是否需要统计专家不断指导,以免落入损失的陷阱。欧熙尼的规则就有这种好处——简单。
工作负荷量变化不断困扰 所有必须依样本来检验其余产品的规则都有一个共同缺陷,不管该规则的用途是什么,它们都受到工作量变动的困扰。有这样困扰的生产经理,还必须烦恼零件供应时有时无的不确定性。他可能因急需零件,而顾不得零件是否经过检验或有无不合格品混入,以致把原来安排好的计划弄得七零八落。一个可能的例外是这样产生的:进来的材料数量很大,质量水准极差,以致全部检验人员大部分的时间都在忙于检验样本和其佘产品。
永远不要没有资讯 采用“不检验”的规则,并不是指要我们没拿火炬就匆匆走入黑暗中。我们应该把所有的进料大概看一遍,也可用“跳批”(skip-lot)抽样的方式,既可找出点蛛丝马迹来,又可与供应商提单上所附的测试值及图表比较。
如果你有两位供应商,就该每家都留一份记录。
更进一步的建议(已在第2章第四要点中提过)是:任何一个项目都要设法和单一供应商建立长期的关系,共同合作,提高进料质量。
服务性组织的错误及其矫正 上述理论适用于事务处理、银行业、百货公司、任何公司的支薪部门及其他情况(参见本章289页例3)。经过各阶段的处理后,最后的结果就会出现在客户账单上,或以支票金额显现,或以对账单方式出现。可能要经过好几个阶段以后,我们才会发现错误,此时矫正的成本可能20倍(或50倍、100倍)于一发生就去寻找并予矫正。在欧文信托(Irving Trust Company)的例子里,k2为的 k12000倍(见下面例3)。
破坏性的测试 前述理论是根据非破坏性测试而来的,测试时不会破坏零件。有些测试是破坏性的,它们会毁了测试样本。例如测试台灯的寿命、每立方英尺瓦斯的热能值、保险丝的寿命,或某抽样纤维的羊毛成分等。此时,对于拒收批进行筛选已毫无意义,因为在测试后已没什么东西可以送上生产线了。
显然,破坏性测试的惟一解答便是在进行零件制造时,就要达到统计控制,一开始就把它做对。这是最好的解答,不论破坏与否。
“全检”或“全不检”规则的应用
例1 某电视制造厂对采购进来的集成电路,一个一个检验。
问:你发现多少个集成电路有瑕疵?
答:“只有一点点。”他看看过去数周的数字后,再度宣称:“平均来说,每1万个集成电路中,只有一两个不合格品。”
据此,我们假设:
p=(1/2)(1/10000+2/10000)=0.00015
进一步询问后,我们得到一开始测试的成本为30美分(k1=30),而且每一集成电路的次装配线都加以一路测试,此时附加价值愈来愈大,若要更换不合格的集成电路,成本为:k2=100k1,因此,p=0.00015<(k1/k2)=1/100。
照理说,该工程师应该不必检验集成电路才对(因为p<k1/k2)。他是在状况1,却依状况2的程序去做。换言之,他正在使其总成本最大化。根据他的检验计划,每个集成电路的平均总成本为k1+ kp,然而如果不检验进来的集成电路,则他的平均成本应为p(k2+k)(译注:小于k1+kp),也就是说差额为每个集成电路损失:
(k1+kp)-(p(k2+k))=k1-pk2=29.6¢
每台电视机里,大约有60~80个集成电路。以每架电视有60个集成电路来计算,如果检验计划选择错误,损失将是每台多花60x29.6=1776,约为制造商成本的10%。
主管工程师一开始就向我说明,他并不需对质量做统计控制,因为他已采取100%检验。他说因为供应商没有适当的仪器来进行厂商所规定的严格测试,他已经做完集成电路的100%检验了。该集成电路制造厂其实相当不差,因为它的不合格率只有p=0.00015。
该工程师的做法反而使公司成本极大化——此为缺乏理论指导时的常见现象,即该工程师做他自己认为最好的工作。看了刚才的演算以后,他才恍然大悟。
顺便一提,该工程师在每组生产人员的工作站前放了一个电视荧光屏,显示该组前一日所犯的每类缺陷数量。这种做法不仅一点用处也没有,更会令人自荨受损,反而有碍于生产(一点也不能帮助别人将工作做得更好)。
例2 某汽车制造商在把马达装进动力传动系统之前,先做了一个测试。我们把此点称为A点。往后,马达就成为动力传动系统的一部分,可以驱动汽车,我们把这点称为B点。在A点测试的成本为K1=$20。马达出现故障而需加修理的成本为k=$40。若马达在B点出现故障而需加修理,成本为$1000。我们再将此成本分为K2=$960及k=$40。通过A点的1000台马达中,有一台会在B点出现故障。问题是:是否该在A点测试马达?我们可列出一张成本表来回答此问题。
该平衡质量为:
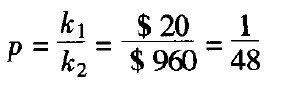
因此,如果有2%的马达在A点出现故障,我们最好继续在A点作100%检验,并试着改进质量,直到在A点的检验应取消为止(由最低总成本判断)。
如果为K2为$500,平衡质量应为p=20/500=1/25。因此,如果p为(例如)1/50,那么在A点进行100%检验和全不检验的成本差异为k1-pk2=20-(1/50)$500=$10。在此情况下,显然最好要中止A点的测试。
表15.1 动力传输系统马达测试
| 是否在A点检验? | 每个马达的平均总成本 |
| 是 | k1+pk+(1/1000)$1000 |
| 否 | 0+p(k2+k)+(1/1000)$1000 |
例3 (纽约欧文信托,拉兹可先生所提供)。在银行、百货公司、发薪部门的工作都是从一个部门传到另一个部门来进行的。每一笔交易在某部门审核(检验)的处理成本是25美分,但如果错误延至最后才发现,而需更正,则平均要花$500=500000¢。该部门的准确性约是每1000笔交易中发生一次错误。所以说:
p≥1/1000
k1/k2=25/50000=1/2000
当P>(k1/k2),也就是在“状况2”时,如果要达到最低平均总成本,我们就要在一开始就进行100%检验。
在服务业进行交易处理时,要找出错误实在很困难(可能比制造业更难)。验证人员可能只能找出一半错误而已,最多也只能找出2/3,所以改进系统就显得格外很重要了(如提高数字的可识别性、灯光照明、招考、晋用、训练及提供统计辅助来监督)。
此时我建议采用第3章介绍过的检验程序,由两人平行计算。两人同时都用清楚可读的备份来计算,确信计算方法和结果没有错误,再将两组数字键入机器,由机器检测有无差异。
就我的经验而言,要验证重要的工作,只有借着平行工作并由机器核对,才是惟一能令人满意的方法。
如果结果的质量远比p1p2好(P1为一位工人的可预测质量水准,p2为另一人的可预测质量水准)。假如p1= p2=1/1000,那么最终结果的质量将会比1/10002=1/106更好。之所以如此,是因为两人犯同样错误的概率极小。但是墨菲(Muiphy)定律说的也没错——任何事如果有可能出错,它早晚就会出错。
我们要鼓励平行工作的两人,一遇到可能误读的数字,就要立即暂停工作,确定清楚。不论追溯数字来源要花多少时间,不论不易判读的数字在何处产生,它们就像一开始就有不合格材料一样糟。
基材有附加价值时的准则修正 我们把要加工的进料称为基材(substrate),并将它的成品加以检验,分为一级品、二级品、三级品或废料。假设K2代表成品降级或报废的平均净损失。检验一项基材进料的平均成本则为k1+kp,若不事先检验基材而致使装配品降级,则平均成本为pk2。在此情形,要满足p值的平衡质量为k1+kp=pk2。由于k=k1/q(见本章310页练习5),它可化成k1+pk1/q=pk2。上面等号左边可用k1/q代入,所以如果P=k1/k2q成立,上式就可满足。
规则现在变为:
状况1 p<k1/k2q 完全不检验
状况2 p>k1/k2q 100%检验
上式的k2现在表示成品因不合格而降级或报废的“平均损失”。
请注意,由于q值几乎总是和1很接近,所以前式与“全不检或全检”规则,可视实际状况而交互应用。
例4 以下为作者送给某公司的一份备忘录,日期如上所示。
我在昨日的会议中获知,上漆钓竿(零件编号42)为贵公司的重要产品,每周产量目前为2万支,而它们很快就会增加到4万支。未加工钓竿的每批进料数目为2800支(批量大小此处并不重要)。
您所提供给我的成本数据,假设已完全依人工、材料、测试和其他费用分摊,其相关数值为:
k2=7¢
k2=1500¢
根据您所提供的数字,贵公司平均不合格率约为1%。因此平衡点为:
p=k1/k2q =7/1500x0.99=0.00471(即略低于1/200)。
表15.2为本人昨日在黑板写下的结论。显然未达到最低平均总成本,贵公司必须对进料钓竿进行100%检验,贵公司目前处于状况2中。
表15.2两种测试方法的2x2成本表
用这两种测试方法交叉测试的结果,产生了图中各点。
| 进料钓竿的检验 | 每件的总成本 |
| 完全不检验 | pk2=0.01x1500¢=15¢ |
| 100%检验 | k1/q=7.07¢ |
如果进料的平均不合格率为(例如)1/300或1/500(平均),就应该完全不做进料检验,而只在成品测试时才检验。
关注您曾提出追踪进料质量必要性的问题。当然,您一定得这么做。为此目的,本人建议您画一张P图,把各类缺陷合并后绘点,并为主要类型缺陷画出另一张P控制图。您可先每批画出一点,稍后可能的话,可每日画一点。据本人所知,贵公司的供应商有意与贵公司共同研究贵公司的检验方法和检验结果。如果能把您现在的P图按月复印给供应商,对他会大有助益,而你也可以向他要控制图。
多样零件
多样零件时,不合格装配品的概率 前面章节只讨论了单一零件的装配品。现在我们参见308页练习4,看看很有用的理论。有些零件为了要让总成本最低,所以需要进行100%检验。一旦检验完成,它们就不会造成装配品故障了。其余的零件将不再检验,但如有一个不合格品流入生产,就会造成故障。假设我们有两个零件未曾检验,其不合格率分别为P1和P2,那么,装配品故障的概率(Pr)为

当零件数目增加时,故障的概率也会跟着增加。一台收音机也许约有300个零件,但数目如何仍将视你怎么计算而定。一辆汽车约有1万个零件,不过,同样还是看你怎么算。汽车内的收音机零件要算一个呢?或300个?汽油泵的零件算作1个或7个?无论你如何计算,在一件装配品内的零件数目都可能非常巨大。
另一个问题是k2(改正错误装配品的成本)会随着零件数目的增加而增加。当装配品故障后,究竟要算是哪一个零件的问题?事实上,误诊太容易发生。更何况,两个零件可能都是错的。
产品愈是复杂,若要想控制成本,就吏需要有可靠的组件。否贝|J,不合格品将影响到整条生产线的支出,如报废、修理、更多的库存(为预防不合格品而准备)、更高的售后保证成本,最后甚至会损及商誉与生意。
因此,当我们采用多样零件时,就面临了下列事实:
1.我们仅能忍受少许零件采全检方式(状况2),否则检验这些零件成本会太高。
2.我们仅能忍受其余零件的质量接近零缺陷。
复杂器材的测试可能需要时间及细心规划,因为器材中的各种组件,可能要在不同的环境压力和时间下,才会故障。
这些问题并不单纯。公司可能采购许多类型的供应品,遭遇到许多类型的问题。常见的一个难题是:有些进料的质量和均匀度对采购者重要无比,可是质量的前后变异却极大。然而,这采购的材料可能只是供应商的副产品,占不到他生意的1%,很难希望他改进。你很难期望供应商为了你而花钱,或买进新的精制设备而冒不赚钱的风险。
对此,我只能建议,把这些材料像铁矿或其他进来的原料那样对待——如果它们进厂时变异很大而纯度不足,你可以在自己厂内精炼或委托外界精炼。此计划在实践上已证实为良好的解决办法。
同样的缺陷重复出现的效果和多样零件相同,任教于麻省理工学院的崔巴士(Myron Tribus)博士告诉我一简单的例子。假设现在的小马达(用在真空吸尘器、搅拌机、家用暖器设备等)在顾客手中的故障率仅为15年前的1/10。可是,现在家用马达平均要比15年前的许多种马达数量多出10倍。因此今日的家电马达故障数目和以前并没有两样。其他例子如下:
某天花板灯泡装置的设计,要用3个特定烛光亮度的灯泡。在家用环境下,一个灯泡的平均寿命大概为3个月,但灯座上要用3个灯泡,所以房屋的主人得准备一架梯子,以备随时换灯泡,平均每月换一次。
再举汽车车体的点焊接缝为例。每一位有过点焊经验的人都会同意,每2000件点焊中有一件错误,已算相当优秀了,自动点焊机也不过如此。可是,即使是这样辉煌的成绩,工厂仍要从事昂贵的测试和车体重修。
假定车体有70处接缝,而点焊机(不论是用手点焊或自动点焊)每焊接2100次就会有一次错误。测试时会发现车体因焊接不合格而漏水的机会为70/2100=1/30。换言之,大约有3%的车体会因漏水而需要重修(还好,很少有会漏水的车体送出工厂)。
要把车体漏水的频率减低至200辆里面只有一辆,点焊机的性能就要改进到每7000个焊点只有一个错误才行。
结论:生产线上任何地方都不准有不合格材料及作工前文的理论 告诉我们,在任一生产阶段都不能容许有不合格品,这是很重要的。任何阶段的产出都等于是下一站的进料。不合格品一旦产生,除非在后站测试时能发现,否则它就会一直存在,直到花了很多费用矫正,或更换为止。
前述理论所说的k1和k2成本,并不是惟一需要考虑的成本。缺陷会带来更多的缺陷。生产人员接到不合格的半成品或装配品时,却会觉得极度挫折。如果她知道自己不论多么细心,产品仍会是不合格品时,怎么会全力工作呢?要是大家都不关心,她为什么要在乎呢?对照一下,当缺陷极少或根本不存在,或是纵有缺陷也能解说充分时,她会了解主管已尽力了,所以自觉有义务要全力以赴,这表示主管们领导有效。
不幸地,缺陷有时就是沿着生产线发生。如良好的零件安装错了,或两根导线交叉接错,或因成品或半成品从一处搬至另一处造成损坏。搬运损坏可能源自粗心大意,或纯属无知。大家也都知道,这种情况在包装搬运时也会遇到。我就看过一卷因人们疏忽致损的影片,如堆高机叉起一车屋瓦,接着撞上钢柱,把屋瓦工人的努力毁于一旦,或把捆袋子的麻绳错丢人石膏内,而非垃圾桶。从来没有人向操作员说明,这些小小的动作会造成多大损失。我就看过一名妇女用镊子小心翼翼地夹着一片磁盘,如同护士在手术房拿着开刀用具小心翼翼,可是她却把拇指放在磁片上,毁了它。如果有人向她说明,她多么轻易就可能毁了磁片,制造磁片的心血就不会白费。我也看过一只全白的鞋子装人盒中时,鞋上有小黑条纹,其余都很完美。只要有人为疏忽,就会造成昂贵的重修或报废。
例外 许多进料并不适用于本章的理论。例如一槽甲醇。你用勺子从槽中任何一处取出甲醇,与槽中其他地方取出的甲醇几乎没有两样。然而,实际上,化学公司是从许多不同的层次舀取甲醇的。就像另一个大家更熟悉的例子——琴酒或威士忌计量杯。大家都知道,不管从瓶子的上、中或下层取酒,其实都无关紧要。
从鼓风炉取出铸水也是一大难题,这是本章理论无法应用的另一个例子。我们明知铸水的成分并不是到处一致的。但是有些公司每铸一件就取一小勺样品。这些样品分析后就能提供数据,画成一张操作记录图,让我们知道从第一件铸件到最后一件铸件的质量变异,同时提供改进线
废除标准验收计划
标准抽样计划 在分批进料或出货的检验中,我们有所谓的标准验收抽样计划。简而言之,它需要测试样本及应用某些决策规则来筛选其余产品,或依样本中不合格品的多寡直接送入生产线。
道吉雷明抽样表所根据的理论是要使检验成本最小化,并达到指定质量的水准。相比之下,我们就很难理解美军标准105D抽样计划的目的,只想到可拿来在供应商质量变差时,拿这本小册子来打他。
哈德(Hald)在本章注释提到的著作中,依其AQL(average quality limit,平均质量界限)把美军标准105D视为抽样计划的索引。有了AQL及批量N,就可以在美国标准105D手册中找到这个AQL的抽样计划。军用标准105D强迫你要指出你所期望的AQL值,却完全没有用到成本数字,难怪有时会令人惊奇——运用105D的结果,竟会比100%检验贵上2倍!
引用任何抽样计划,虽然其原先的目的是想降低进料质量的平均不合格率(本章中用p表示),最后都只会增加上述单位产品的最小平均总成本(请参见本章后的练习5)。
如果有一家某公司用AOQL(average outgoing quality limit,平均出厂质量界限)为3%的标准采购货物时,这无异是明示供应商他的要求是100件中要有97件合格品及3件不合格品。供应商会很乐意接受这种要求的。
例如,最近有家制造商告诉我,他的目标是送给客户的不合格率不要超过3%。有些顾客会收到远高于此数的不合格品。这样做生意好吗?你会是那个愿意接受不合格率水准不高于3%的客户吗?
不幸的是,标准验收计划在统计质管的教科书中占了很重要的地位,我自己的书中谈到抽样时,也不例外。安士孔伯说:“我们要了解问题的症结所在,设法解决,而不是想出一种看似能确切解决问题却与原问题并不相关的代用方法。”
现在是扬弃这种计划及其训示的时候了,让我们着眼于总成本问题及实务。
标准计划的形式化应用 道吉雷明验收计划或美军标准105D手册的使用者,大部分恐怕只想求形式上能符合合约规定而已。订立合约的是由不够资格起草计划的人起草的,而由另一批同样不够资格的人负责执行。大家都这样做,我们也跟着做,结果是增加了成本。费根堡说:
最大的问题是……不智地使用这些验收计划,应用在不适合它们应用的地方。
例如,如何用美军标准105D来增加成本。某出货批量为1500件装配品的制造厂送来分组合件。此分组合件每次大概要花2小时来检验,平均成本为每装配品24美元。原厂的生产过程平均不合格率为2%(最近收到此批的经验证实了质量资讯无误)。如果在最终检验时,再取代不合格零件,总共则要负担780美元。我们究竟该用哪一种抽样计划呢?在本例中,
p=0.02<k1/k2=24/780=0.031
这显然是属于状况1的情况。所以为了达到最低总成本,我们完全不检验。若使用刚刚说过的美军标准105D,则会使总成本等于最小总成本的两倍。我们很容易就可以在310页练习5的结果中看出来。
还有更糟的事呢!要是生产过程是在良好的统计状态之下,则测试样本不会提供有关批的资讯,充其量是碰运气而已(参见练习1)。
量测及材料上的其他问题
次装配品构建的可能经济 上述理论所说的k2成本,通常都会随着生产线各阶段的工作而急剧上升(也许是10倍),到成品时,数目可能已相当惊人。有时候,我们可借着构建“并流”到最终装配品的次装配品,避免极高的成本。一旦几个次装配品,经过检验及适度的更换和调整后,就会形成新的起点。此时,前述理论中的k2成本就成为检验及调整次装配品的成本。这些理论再加上有意义的历史记录,就可显示出哪些次装配品根本不需要检验,哪些需要粗略的100%全数检验,以避免出现更高的成本损失。在此情况下,本章理论即可作为指导。
我们前面之所以不厌其烦地讨论,只是想告诉读者,用对了理论来指导,就几可达到最低成本和最大利润。
同时,我们要尽全力来除尽不合格品。我建议采用有系统的做法——将我们的测试结果与供应商的测试结果加以比较,辅以恰当的统计方法,诸如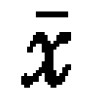 图及R图等。
图及R图等。
能够与零件(尤其是重要的零件)供应商顺利合作,并有效地测试和调整次装配品,可以减少最后成品测试中的重大麻烦(到几乎没有)。
有些少见的缺陷很难找出来 随着不合格率的减少,我们愈来愈难找出这样小的缺陷。“检验”毕竟不能找出所有的瑕疵来,特别是当它们很少见时,不管是用目测检验或机器检验都很难。我们没有理由相信,一家宣称其不合格品有1/10000件的制造厂会确实比另一家不合格品是1/5000件的厂商来得更好,因为这两种情况下的不合格率都很难估计。
因此,当P为1/5000时,如果生产过程在统计控制下,我们可能要检验8万个零件,才能找出16件不合格品。根据此数字,我们可知生产过程的估计P值等于1/5000,标准差为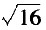 =4(或称25%)。这样估计出来的不合格比率并不精确——尽管我们已检验了8万个零件。我们甚至会怀疑生产过程在此过程中是否稳定?生产过程产出8万件后是否和开始生产时相同?如果不相同,那么该16件不合格品有什么意义呢?这个问题就难回答了。
=4(或称25%)。这样估计出来的不合格比率并不精确——尽管我们已检验了8万个零件。我们甚至会怀疑生产过程在此过程中是否稳定?生产过程产出8万件后是否和开始生产时相同?如果不相同,那么该16件不合格品有什么意义呢?这个问题就难回答了。
在有些情况,100万零件中没有一件不合格品,甚至在10亿件中,都很少有不合格品或根本没有。当不合格率如此低时,我们不管对最终成品要做多少检验,都很难得到必要的资讯。在这种特殊要求下,惟一可能的办法就是使用生产过程中实际量测零件的控制图。如每天取100个观测值(每天25次,每次连续取4个样品),在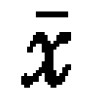 图及R控制图就能画出25点样本,大小为4的平均值和全距值。控制图会告诉我们生产过程一直都没有改变,或已出了差错,或是该暂停一连串的产品,直到找出问题原因为止。一旦找到问题原因,就可合理决定,究竟是把全部产品废弃或放行一部分。如此,立即可以看出无与控制图的相乘威力。
图及R控制图就能画出25点样本,大小为4的平均值和全距值。控制图会告诉我们生产过程一直都没有改变,或已出了差错,或是该暂停一连串的产品,直到找出问题原因为止。一旦找到问题原因,就可合理决定,究竟是把全部产品废弃或放行一部分。如此,立即可以看出无与控制图的相乘威力。
使用复连法(redundancy) 在设计一件复杂的器械时,有时可把两个或更多的零件并联,假如其中一个发生故障时,另一个会自动代替,这是聪明而可行的方法。把两个零件并列相比,如果每一个平均不合格率各为pi,相当于一个平均不合格率为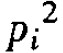 的零件。假设为1/1000,则
的零件。假设为1/1000,则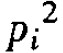 为1/1000000。当然,有时基于重量及大小限制,我们不能用这种复连备份。但另一个问题是:在需要的时候,这些多出的零件会适时介入,发生作用吗?因此,最好的解决方式仍是在于高度可靠的单一零件。
为1/1000000。当然,有时基于重量及大小限制,我们不能用这种复连备份。但另一个问题是:在需要的时候,这些多出的零件会适时介入,发生作用吗?因此,最好的解决方式仍是在于高度可靠的单一零件。
故障的数学理论及复连的理论是很有趣的,同时它们也是很重要的统计技术,因本书篇幅有限,只好在此稍作论述。
便利的检验法是否真的较便利 在必须进行检验的地方(如状况2),“如何削减检验成本”是一个长期的老问题。假设除了原来的检验法之外,我们尚有一个令单位成本较便利(k1值较小)的检验法。但考虑总成本时,便利的检验法是否真的便利呢?针对非破坏性测试为例,我们可用两种方法各测试200个项目,并把结果做成2x2表(如图15.2)。图中每一点都代表同一零件用两种方法的测试结果。落于对角线的上点表示两种方法测试的结果一致,偏离对角线的点表示不一致。一个零件可能通过便利的方法,但为主检验法所拒(称为“误正”,a false positive),将会造成装配品k2元的故障损失。另一方面,零件通过主检验法而被便利的方法所拒收(称为“误负”,a false negative),会因此而增加成本!(u为一个零件的成本)。
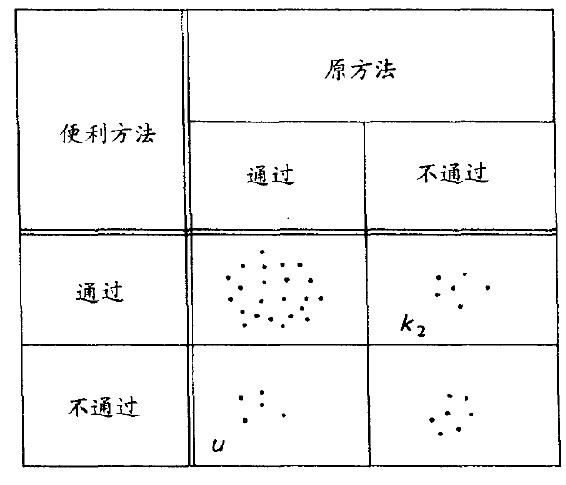
图15.2全不检及全检的成本比较
我们很容易就把2x2表的结果,量化为下列4个方格内的数字:
n11 n12
n21 n22
假设以主检验法量测200个项目的成本为M,用便利法量测出来成本为C,那么使用便利方法可节省的成本为:

图中远离对角线的数目通常很小,因此会有很大的统计波动。一方格内,离开对角线的某数目的标准错误(standard error)通常会很接近数目本身的平方根。如果某数字的数值为16,则其标准误为4;若数目为9,则标准误为3(上述假设是根据差异的泊松分布而来)。
如果我们怀疑便利方法是否确实比原法便利,则可再测试200件,甚至再测400件,以求精密。如果还有疑问,我建议最好仍用原来的方法来测试。
多样零件 上述的建议和计算,只适用于单一零件。假设该装配品含有两个以上的零件,而我们考虑为每一零件找出一个便利的方法,事实上可将上述计算应用到任一零件上,不管数目多少,都可根据它得出一个决定。
不过,我们要小心。用便利法测试任一零件,都要从装配品中选择一件来测试。此种选择是从图15.2右上方的“误正”所引起的。其中有些任一零件的选择可能会和其他零件重叠,但是随着零件数目的增加,装配品的测试比例也随之增加。因此,假设我们有20个零件,每一零件都用便利法测试,如果它在20次中会有1次的“误正”机会(举例而言),因“误正”而测试装配品的比例为:
1-(1-0.05)20=1-0.36=0.64
如果装配品是由零件串连而成,那么装配品万一出现故障,我们就可能必须测试装配品上所有的零件。
本节旨在说明,由测试所造成的麻烦可能会比产品本身更多。工业上有许多产品被判为不合格,主要就是因为量测过程的结果不一而造成。
不管是使用原方法或便利方法,这两者都必须在统计的管制稳定状态下才能比较,否则就容易导致误解。
改进2x2表来保留资讯——两位验证人的比较 我们现在把50项产品分别送交甲乙两位验证人,以观察两人的结果是否相同。验证工作是对顾客及制造商双方都有保障的做法。每一位验证人把该项目分为最高级或普通级,并把该50项的测试结果依照验证员的测试次序,分两栏记在相对的50行上。
为了有更多的资讯,我们不依图15.2的方式,把每一对测试的结果用某点来表示,而是按每一项测试次序,把项目编号记在适当的方格内(如图15.3)。
我们可以看出,在右上方的格子内有4个连续数字(35、36、37、38)。这种现象发生的概率非常低,可能表示某不一致的特殊原因。因此,假如10次测试有1次落在右上格内,则连续4个数宇的连串出现的概率只有1/103。
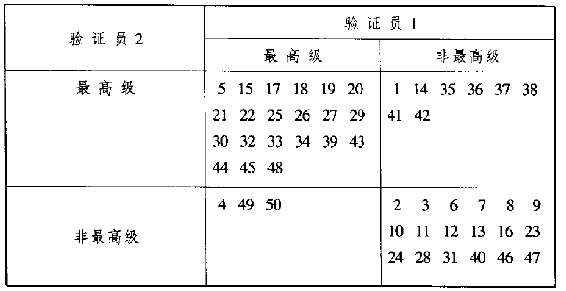
图15.3 50个项目的2x2表
项目编号如图所示。本图与图15.2不同之处在于:本图以实际编号表示,而前图则以图形表示。
便利筛选法的应用 发病率的调查有一知名的计划,有时可能在测试上很有用。假设经计算后,显示pk2>k1;采用100%检验法测试零件,可得出最低总成本。但是我们有一便利方法可用,并且可以调整至不会接受原方法所拒收的零件。我们先用便利法筛选n个零件,然后再将这批零件分为两类:n1个接受及n2个拒收,如表15.3所示。
我们可放心地把便利法判为接受的n1个零件送入生产线上(依假设,我们可以调整便利法使其如此)。接下来,用原方法测试被便利法判为拒收的n2个零件,结果则如表15.4。
表15.3 便利测试法

表15.4 原方法总数

如果用原方法测试n2个零件的成本不致太高,则此计划将可使我们的费用大为节省,计算方法很简单。假设:
k1=用原方法测试一个零件的成本
k1’=用便利方法测试一个零件的成本
筛选后,我们将可节省:
D =n k1 -nk1’-n2k1
=n(k1=k1’-n2k1/n)
上式括号内的数量为每单位的差异。举例用数值说明,假设:
k1 =$1.20
k1’=$0.10
n2/n=0.4
则其差异为:
D=n(1.20-0.10-0.4x1.20)=62
上式表示我们约可节省一半的费用。
应用尺度法来作比较的优点假如这些测量值是用某类单位来表示——如厘米、克、秒、安培或其他单位,那么我们就应该用更有效率的比较法。我们可将个测量值的结果画在xy平面上。
图15.4包含4种原方法与便利法的可能比较。此法可比图15.2的2x2表更有效率,因为它只需要远比图15.2较小的值即可做出决策。落在45度直线上的点,表示两种方法的结果趋于一致;不落在对角线上的点,即表示两种方法不一致。研究该图,可以让我们迅速地指出两法是否有差异、相差多少。对于熟悉两种方法而又技巧熟练的人而言,调整便利方法使其与原方法吻合可能并不困难。
另一可能性是,在图15.4的图B状况下,我们不去调整便利的方法,而将其读数转化为原方法。因此,我们假设:
y’为以原方法得出的测量值
y为同一物品用便利方法得到的测量值
m为两个方法最佳配合的回归线的斜率(假设其关系呈直线)
b为y’轴上的截距
以图15.4为例,其B情况可转换为:y’=y+mb。
顺便一提,即使两个方法的结果一致,并不表示两个方法都对。两个方法一致只说明了测量系统确实存在而已。图15.4的图C就很有趣。图中画出的直线斜率小于45度,所以该斜线表示便利方法比原方法更敏感。如果它始终保有这个优点,我们就应抛开原方法,而调整便宜方法后采用之(此点由Peter Clarke 1983年11月在开普敦举办的研讨会上首先提出)。“斜率大于45度”时,表示便利法较不敏感。接下来,我们就可以y’=y+mb。(m为斜率)这个方程式来调整便利方法为原方法。西方电气公司1956年出版的《统计质管手册》的B-3节,对仪器精密度及测量误差就有极详尽的探讨。
检验时形成共识的危险 如果大家都能坦诚无惧地交换意见,而达到一致的共识,就能得到团队的好处以及相互学习的优点。
不幸的是,在检验或其他事情上,“共识”可能只表示了一人独排众议的结果,其实只是他个人的意见而已。
譬如说,两位医生也许在某病人的病历上都显示出意见一致的情形,如提高、未提高或恶化。该结论可能只代表了年老医生的见解,因为年轻的医生以能与老前辈会诊为荣,前辈所言,言听计从。如果年轻医生意见太多,就不会形成这种和谐的关系。(也许年轻的医生是个实习医生,为了明年再留任,只好唯唯诺诺,谨慎发问。)
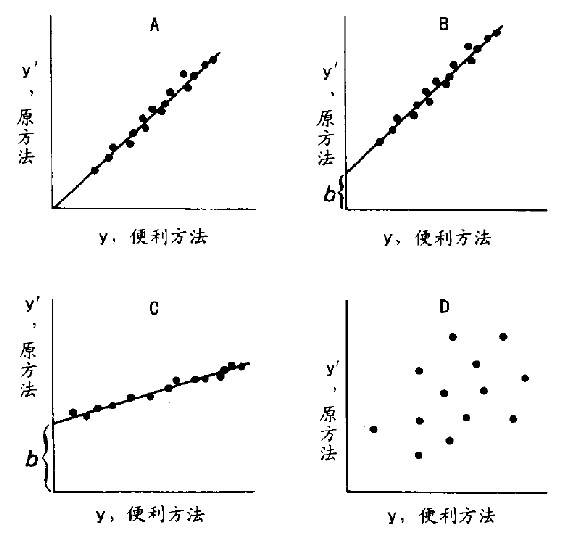
图15.4 原方法与便利方法比较
以两种方法交叉衡量某一项目,就会在图中产生一个点。45度线上的点表示两种方法完全一致。图A中,点在45度线上或很接近,表示两方法相当一致。图B中,线的斜率接近45度,但有截距。使用某些简单的调整即可使两方法趋于一致。图C中,线的斜率与45度线相差很多,且有截距。某些简单调整或可使两方法一致,或者可用简单公式校正便利方法。图D中,点在图中到处散布,表示问题很难解决。
更好的做法是每人都在个别的一张表上记下他个人诊断的结果(提高、未提高或恶化),方便的时候,再加以比较。如此一来,年轻的医生就可对其看法异同单独提出问题。换言之,这种方式可使年轻医生不怕问问题。图15.5的简单表格,就显示出其异同的诊断结果(此法为作者在I960年左右,应纽约州立精神病学院卡尔曼(Kallmann)医生之邀所做的咨询)。
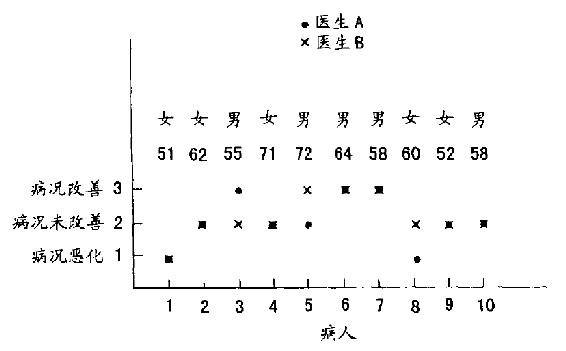
图15.5 两位医生的诊断记录图
如能依病人类型来研究医生彼此判断的一致性,可能更加“知己知彼”,从而达到近乎完全可靠的共识。图上简单标示病患的性别和年龄等,可指示出这个年轻人哪里需要帮助。
在此一提,两人对于个人独立所做出的判断如结果显示一致,也只能说他们之间形成了一套系统,并不表示两者都对。答案无所谓对错,除非他们用的是专家一致认同的方法。
两检验员的比较 多年来,两位皮革检验员对每一束皮革进料样本检验的结果一直保持一致。我们向他们解释过后,他们立即了解形成共识的危险,并同意分别记下他们自己的看法以作比较,同时在结果偏离时,互相探讨学习。
皮革的等级分为1、2、3、4或5;第4等级表示最高级。评等级计划如下:
1.每位检验员从每一批货中抽取一张皮革,上、中、下方各取一张,分散取样(这就是我们所说的机械式抽样,非随机数抽样)。
2.每一位检验员各自独立检验自己所选取的皮革,并记下等级。
3.两位检验员要独立检验第20张皮革,记下结果(他们轮流抽样)。
4.将结果画成图表(如图15.6)。
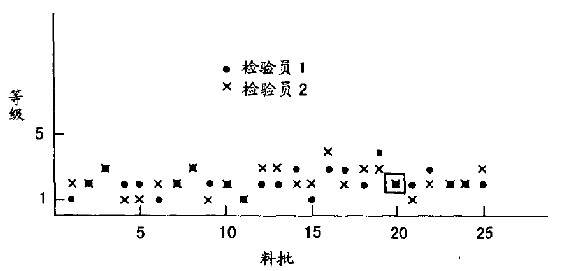
图15.6检验员独立工作的结果
此图说明两者没有明显差异。图中第20点的小方框表示,实验设计使两检验员检查同一张皮革。
两组结果的差异原因可能有两个出处:(a)两人之间的差异;(b)样本的差异。结果:没有显示什么大差异(近一年下来),两位检验员的判断还不致于南辕北辙。对于第20束的检验结果,几乎如出一辙。其他的应用则显示需要有更清楚的定义才行。
我们要再一次强调,两者一致并不表示他们都没有错,而是表示抽样和检验方法构成了一套分等系统。
进一步说明图示 图15.5及图15.6的表示法可适用于4个或5个检验员的情形(6个检验员则会太复杂)。同样,我用3个符号●、〇、X来表示从炼钢炉中所倒出的12炉样本,在(1)开始时(2)中间和(3)结尾时所抽出的样本。在某实际个案中,只有一处〇和X重叠。此重复出现的关系显示了两种可能:(a)炉内的组成成分未能充分混合,或(b)混合物在生产过程中有老化现象。
练习、说明、结论
练习1假设我们面前有一碗红珠和白珠,P为红珠子的比例,q为白珠子的比例(图15.7)。
步囅1 从碗中随机抽取每批数量为N的珠子(取出后再放回)。结果是:
N 总数
X 红珠
N-X 白珠
步骤2 随机抽取样本大小为n的珠子,不再把珠子放回去。结果如上图的方框。
步骤3 将前一步骤抽取的样本珠子放回批中。

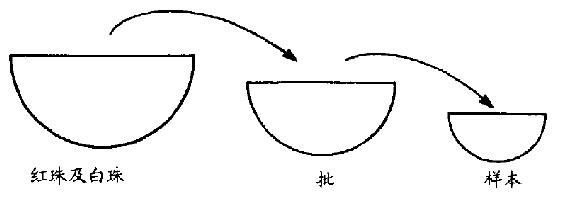
图15.7红白珠抽样
从红珠及白珠中抽出数料批来,再从料批中抽出一样本。放回从料批抽出的珠子,可保证每次从料批中所抽的红白球比例是固定的。
步骤4 重复步骤1、2、3多次,保持每次批量(N)及从其中抽取的样本大小(幻固定不变。记下r和s的结果。
我们可从理论导出r和s的分布为:
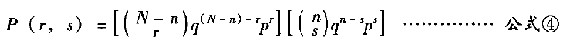
结论 (a)样本(大小为n)中的红珠数以及批中剩余部分的红珠数都是呈同样比例p的二项分布,及(b)这两个分布都是独立的。也就是说,剩余批中红珠数r的分布和样本中的不合格品是s=17或是s=0,其分布都是完全相同的。
此定理真是令人吃惊。它告诉我们,如果个别不合格项目是独立的,它就像生产过程在相当良好的统计控制状态下的情况。那么,不管我们怎样卖力设计验收计划,结果都和掷铜板从选批中剩余部分来筛选一样(掷铜板还比测试来得便利)。
除了从批中抽取样本外,我们也可选用随机数,将批分为两部分:样本和剩下的部分。
练习2 如果各批中不合格品的分布比二项分布还要紧窄,而且批的其余部分的接受准则假定是根据样本的测试而定,那么接受剩余部分的准则应是:当样本中有许多不合格品时,其余的部分就该接受,不予检验;若样本中不合格品极少,甚至没有不合格品,就该拒收并筛选其余的料批(并非我们平常看到的相反规则)。
我们有一简易法可了解上述结果,即假设所有进厂的各批物品都有一样数量的不合格品数目,所以说,不合格品不是在样本中,就是在剩余批中。因此,要是样本中有大量的不合格品,就表示剩余批中不合格品的数目很少。
希尔(I.D.Hill)为文指出:有一简单办法可以生产出质量均匀的批。假设有20台机器都制造同样的产品,19台全部生产合格品,其中1台生产的全是不合格品。如果我们由20台机器上各取一件产品,那么凡是以此20件产品为倍数所构成的批,其不合格率必然是5%。
各批质量保持一定的事情并不少见。譬如有一套(假设12件)轮流冲压金属板的齿轮掣子(pallets),有一个掣子出现故障了,结果它所冲出的产品几乎都成了不合格品,其余11个掣子则完好无损。所以在这连续12个产品所构成的批量中,总产出的不合格率就很接近1A2(或8.3%)。
练习3 100%全数检验或全不检验规则的证明。让我们用随机数从批中随机抽取一个零件,并把它叫做“零件广。它可能是不合格品,也可能是合格品。我们应该检验它吗?或是直接送上生产线不加检验(我们把平均总成本整理成如表15.5)?
表15.5 零件全检或全不检

我们注意到,假如P=k1/k2,则上述两种检验的答案都是相等的。木德(Alexander Mood)称此一质量为“平衡质量”(break-even quality),也就是说,处于平衡质量状况时,检验和不检验的总成本相等。我们进一步看出,假若p>k1/k2,则“检验”的总成本较低(见图15.8)。
显然,假使下个星期(举例而言)进来“最坏的批”会落在平衡点的左边,那么其余各批就会比它更好,而且愈来愈往左边去。在此种情况,不检验可达到最低平均总成本,我们称此状况为状况1。
另一方面,假使未来进来“最好的批”落在平衡点的右边,则所有各批都会更糟,愈来愈往右边去,此为状况2。此时所有各批都加以100%检验的结果是:可达到最低平均总成本。
所以说,图15.8中的折线OCD表示最低平均总成本。随着p值愈来愈接近平衡点B时,100%全数检验与全不检验的成本差距就会愈来愈微小。
练习4 多样零件的最低平均总成本。假设我们现在有M个零件,并假设pi为零件i的平均不合格率,而ki为检验一个零件的成本。每一装配品故障后所产生的额外成本将用K来表示,又假设每一零件的K值都相同。(由于我们要用来表示检验2号零件的成本,所以必须稍微转换符号表示法。)我们究竟是该检验所有的零件呢?或只检验部分零件?如果只检验部分,哪些该检验呢?(应用291页公式③的近似值。)
100%全部检验与部分检验的成本差异,将会使我们偏爱部分检验,其数值为:
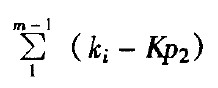
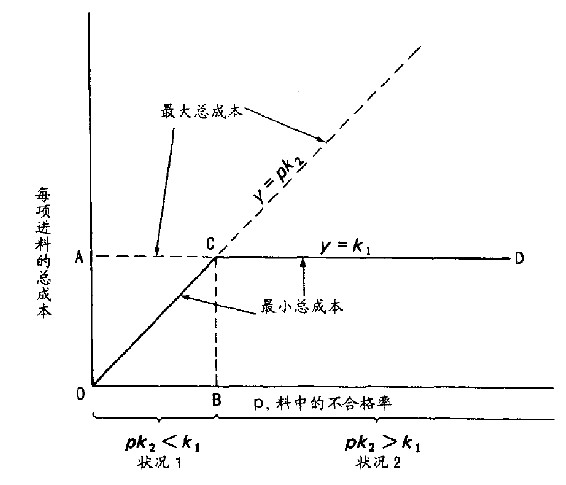
图15.8 有不合格项目料批的每项目最低总成本等于进料质量P的函数
最少不合格率以OCD折线表示。线OC在平衡质量点B(p=k1/k2)处转折。如果不检验可使成本最低,那么此时采用100%会使总成本最大化,反之亦然。
要使总成本最低,我们该检验哪些零件,不该检验哪些零件?换言之,我们如何使全检和部分检验的成本差异最大化呢?答案很清楚。让我们按大小(从大到小)逐项排列下述M值:
ki-Kpi,i=1,2,3……M
这些数值会先从正值开始,然后渐渐递减,经过零,再向下继续递减。为了达到最低平均总成本,上式中各项的总和必须愈大愈好。因此,最低平均总成本的规则将为(如表15.6):
- 对那些ki-Kpi为正值的零件不必检验。
2.对那些ki-Kpi为负值的零件全数检验。
表15.6 求取多种零件的最低平均总成本
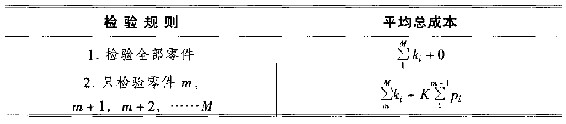
我们要先和供应商协力使各零件都在统计控制状况下,以降低pi值。果能如此,总成本则可降低,从而可不时把某些零件放宽为不必检验。
说明1:从微小的负值转为微小的正值时,成本只会稍降,但是从大的负值大幅偏移为大的正值,则会使成本大大的降低。
说明2:我们可以说,每一零件都有一个平衡质量(定义为pi=ki/K)。因此,我们对多样零件的结果,只不过是重复单一零件的计划一及计划二而已。
说明3:某零件的不合格率分布若跨越在零件的平衡质量左右,则我们将会把它视同单一零件。
说明4:任何零件若非处于相当良好的统计控制状态下(它显然是在混乱状态),则必须采用100%检验。
练习5 (本练习旨在说明,假若进料质量在平衡质量的某一边相当明显时,如果不采用“全检或全不检”,而采用其他检验计划,都可能会令总成本大增。)假设进料项目的平均不合格率为p,我们从批中抽检f部分(fraction)。如果我们随机抽取(例如用随机数表)检验项目,那么检验每项进料的平均总成本,以及由于不合格项目而造成装配品要重测及重修的额外成本将会是:
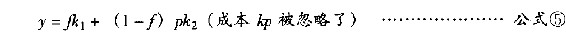
问题是f值应该是多少才可使y最小。我们首先注意到:当P=k1/k2(平衡点)时,不管f值为多少,y总是等于k1。
要是在平衡点的左侧,公式就变成了P<(k1/k2)。此时我们干脆把公式⑤重写为下述形式:

显然,如果我们让/值在平衡质量的左侧,从0到1之间做变动,那么y将从最小值渐增至也就是说,在平衡点左侧(p<k1/k2)的任何检验,都将增加总成本。我们可以很容易看出,位于此区域的接受计划,可能会使最低总成本增加2到3倍。
现在让我们来探讨平衡点的右侧,即(p>k1/k2)时的情况。我们可以重写公式⑤为:

如果我们在此区域让/值从0变动到1,则y值就会从pk2下降至最小值k1。也就是说,在平衡质量右侧进行100%检验时总成本最低。如果我们并未进行100%检验(即f<1),则平均总成本将会大于最小值。
除296页拉兹可所举的例子外,我们现在再讨论另一个例子。
示范说明的例子 某公司所收到的进料铝片每批有1000片,是用来生产硬磁盘的。我们收到进料的第一步是先从批里随机抽65片,采目测方式检验。结果显示,凡是未能通过目测检验的铝片,若送上生产线,必将引起成品磁盘的故障。所以凡是目测来检验不合格磁盘的都要用良品来取代。
未能通过目测检验的产品平均不合格率大约是40片里面有1片,即0.025。其抽样的拒收规则是,如果样本中5片以上不合格(5片是3个标准差的上限),则全批拒收。记录显示,只有很少的进料批被拒收。我们因而可假设在最近的未来,质量水准尚可称维持在统计控制状态。
看得出来有目测缺陷的不合格品流入生产线的平均比率为:
0.025 -(65/1000)x0.025=0.023。
每片铝片的目测检验成本(充分分摊以后)则为7美分。
在准备目测检验的时候,会因为搬运而毁损1%的铝片,检验本身也会毁坏一些。
上述测试仅包括眼睛看得到的缺陷而已,其他未能目测找出的缺陷,都会造成在最后测试时100片硬盘中有1片失效。这些都是普遍而常见的非制造成本,不管进料由目测法检验出的不合格率有多少(既然它与下文的决策成本表无关,因此我们就从表中省略了)。
制造出磁盘成品的附加值为11美元,铝片的成本为2美元,总共是13美元。磁盘成品出现故障时,原料铝片可回收,因此磁盘成品不合格的损失为11美元(不计回收成本以后)。假设:
f=进料抽检的百分比率(=65/1000=0.065)
k1=每片产品的目测检验成本(=70)
B=每一片铭片的购入成本(=$2)
k2=每一产品的附加价值(=$11)
p=以目测法可找出的平均进料不合格率(=0.025)
p’=非目测缺陷的磁盘的平均损失(=0.01)
p”=未能通过目测检验,却流入生产线的平均碟片比率(0.025(1-65/1000)=0.023)
F=因准备检验而搬运损毁的磁盘比率及检验本身损失的百分率(=0.01)
现在我们可以备妥表15.7来预估成本。
表15.7零件检验的结论

结论:由于现行检验法差异甚大,因此我们建议立即换方法。即使在不合格率及成本与表15.7相差颇大时,此一建议(使用100%检验)仍属有效。
同时,我们还要与供应商共同努力,继续提高进料质量,以期能使不合格率低于平衡点,而不需目测检验,节省营运及处理磁盘的成本。
注意:本例的平衡质量并不像本章前文的简单分数(k1/k2),但我们并不打算作更复杂的探讨。
练习6 试说明某公司对供应商采取的进料检验方式是否徒劳无功?
我们靠抽样检验来决定是否收下进料,只要有一个不合格零件就全批拒收。
评论:(1)实际发生的情况是:不管有没有检验,大多数的料批都会直接送入生产线。因顾客需货甚急,不愿再做检验或退还供应商。(2)如果k1>pk2,则检验的总成本将比不检验者为多(毕竟我们没必要增加成本)。(3)如k1<pk2,就进行100%检验,而不用抽样方式检验,才能减低总成本至最低。(同样,我们何必增加成本?)(4)如果进料质量的分布严重超出管制之外,而且分布在平衡点两侧,那么最好采用100%全检或用欧熙尼规则(见285页),然后赶快脱离这种惨状,我们可以和供应商合作以改进质量,使其达到状况1(k1<pk2),并且尽可能持续提高至零缺陷。(5)简言之,上面引述的要求不合时宜且无功效,只会花大钱买到坏质量而已。
练习7 值评估法。假设我们从S供应品中抽取出一件零件加以检验,其成本与从批量N中抽取一件加以检验的正常成本相同。又假定xi=1,表示零件为不合格品。xi=0表示零件没有不合格品。现在假设xi=1,也就是说,零件xi为不合格品。我们必须从供应品S中抽取一件并加以检验,其成本为ki。此抽样可能仍为一不合格品,此时我们再抽验一件,继续下去,一直到我们抽验到合格品为止。我们可将这些可能性画成图15.9的概率树(probability tree)表示。
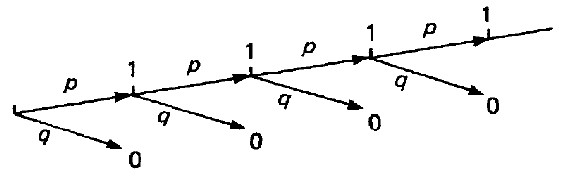
图15.9 概率树
检验某一零件,使得概率p至xi=1,不合格;也同时使得q至xi=0,非不合格。
平均成本k显然为:
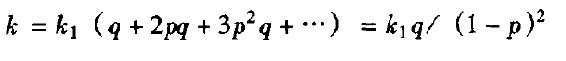

此时,
q=1-p
检验一件产品项目及以合格品来替换不合格品的总平均成本为:
k1+pk= k1/q 由于p在绝大多数的应用实例中,数值都很小,而q值很接近1,在这种状况下,我们可用k1来取代k1/q。
练习8
N=批内的件数
n=样本中的件数(假设我们使用随机数从批中抽取),并用合格品替换不合格品。
P=进料平均不合格率,此数字p值可以粗略预测以后数周的平均值。
q=1-q
p’=因拒收而加以筛选的料批的平均不合格率
p”=料批接受后直接送上生产线的料批的平均不合格率
k1=检验一个零件的成本
k2=因不合格零件流入生产线,使装配品失效,而必须分解、修理,再装配及测试的成本。
P=在初次检验时,就遭拒收的料批而待筛选的料批的平均比率。
Q=1-P在初次检验时就接受的料批的比率。
不论验收计划如何,我们可确定:
若n=0则P=0和Q=1
若n=N则P=1和Q=0
让我们看看实行验收计划后,平均料批将会成为怎样的情形。
n 进入生产线而没有瑕疵的零件
(N-n)Q 不经测试直接送往生产线的零件数,平均质量为p。
(N-n)P 拒收并筛选的零件数。它们全部都是合格品,直接送入生产线。
(a)每一零件的总平均成本为:
C= k1[1/q+Q(k1/k2)(P”-k1/k2)(1-n/N)]
(b)若p< k1/k2,则Pn-k1/k2将为负值,此时我们若设定n=0(状况1)将会达到最低的平均总成本。
(c)若p> k1/k2,我们如能找出一个验收计划能使Pn-k1/k2成为负值,则平均总成本将小于100%检验的成本。
(d)即使我们很努力,但找到的验收计划的值却一直是正数,总成本将比100%检验时的进料零件还贵(与练习5同,它们都是我们应尽力避免的陷阱)。
本章附录
零相关的实验示范:生产过程在统计控制状态中,样本的不合格品数目与批中剩余部分的不合格品数目零相关。
我们可将第11章的红珠实验(236页)稍加修改,大略显示一下批中抽出样本中的不合格品数目与批中剩余部分的不合格品数“完全没有相关”。
此实验的数学证明在306页练习1的公式④中。同样的实验显示出样本与批之间“稍有相关”。
我们仅须把实验中全批50颗珠子分为两部分,一部分是样本,另一部分为剩余部分(图15.10)。每次把每一批中的红珠与剩余批中的红珠数算清楚后写下来,然后把50颗珠子放回批中,搅匀后再抽出新的一批。
让我们先说明某些记号的意义:进料批的大小经常为N,其不合格品数在平均值p附近呈二项分布。从每批中(N)中抽取固定大小的样本n(不再放回去)计算每一样本及剩余母体中的不合格品数目。假定s为样本中的不合格品数,r为剩余批中的不合格品数,那么s和r都是随机变数,其联合分布(joint distribution)则如306页的公式④所本。假设:
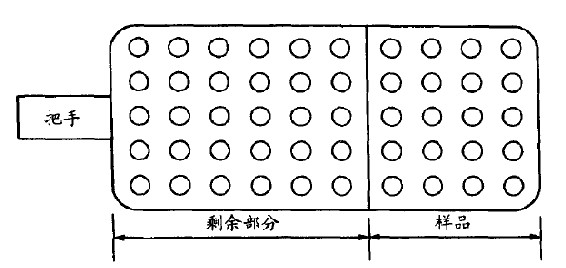
图15.10 红珠实验
以一支有50个洞的把勺,从许多红白珠子中以机械抽出50个珠子。我们将其中20个珠子视为样本,30个为剩余部分。

变异数Var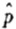 和Var
和Var 会随着N和n的增加而变小。所以从大的批中抽取大样本,将可提供有关剩余批中的不合格品数的信息,也可提供有关批中不合格品数目的信息。
会随着N和n的增加而变小。所以从大的批中抽取大样本,将可提供有关剩余批中的不合格品数的信息,也可提供有关批中不合格品数目的信息。
再者,我们可能在计量塑问题(enumerative problem,目的是希望从样本中了解批的特性)中,运用抽样理论来估计批的特性及这些估计值的标准错误。
现在我们看一下一定大小的批量和样本与实际结果有什么不同。图15.11、15.12、15.13和15.14显示出:在不同的N和n值下,二项分布的样本和剩余批中的红珠数。各图的样本和剩余批其实都是从同一批中而来的(每批都有100个样本)。图中清楚显示:样本和剩余批并无相关。然而,样本数愈大,样本及剩余批中红珠的比率估计就愈准。因此,图15.14(样本大小为n=1000,而剩余批的大小为N-n=9000)清楚地指出样本愈大,对整体(样本加上剩余批)及剩余批的估计会更准——即使样本和剩余批并不相关。图15.11~15.14说明了统计理论的一大特色就是,只要样本够大,我们就能从单一样本中精确地估计出整体的特性(找出95%)。因此,抽样理论有助于我们估计剩余批及全体的特性估计及这些估计的标准错误。

图15.11 N=50,n=20。此处样本与剩余的数量不会差别很大,它们分别为20及30。此图显示样本中红珠的比例与剩余批红珠比例之间并无关联。
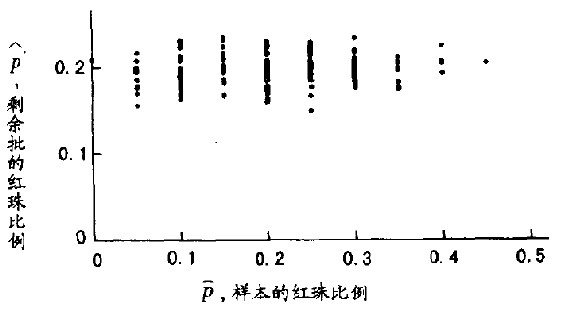
图15.12 N=600,n=20。此处剩余批红珠的比例变异显然远小于样本中的变异。理由是剩余批的数量为N-n=600-20=580,大于样本的许多倍。此处样本中红珠的比例与剩余批中红珠比例之间的相关性再度为零。
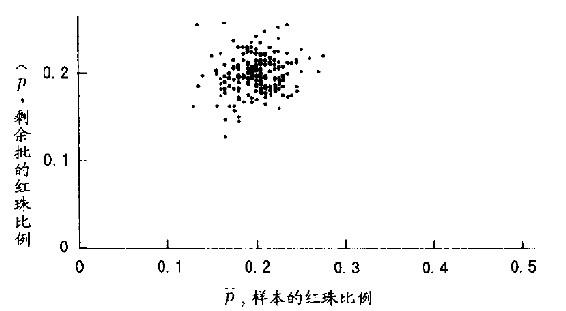
图15.13 N=600,n=200。此处我们可以看到当样本数增加为200,并将剩余数量减至400时,结果会变成怎样。此图正如前者,样本与剩余红珠的比例相关值仍为零。
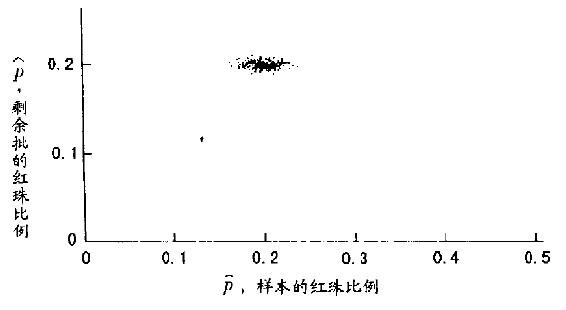
图15.14 N=10000,n=1000。两者再度显示彼此仍不相关。
