谴责比忍气呑声好得多;而认错者可免受伤害。
——《圣经•旧约》
本章目的 通过举例说明“干预(tampering)将会导致损失”的理论,也就是“结果管理”的缺失。
任何人都可以用漏斗进行以下的实验。
所需材料
•漏斗一个。一般厨房用的漏斗就可以,因为这并非是实验室的实验。
•可以很容易通过漏斗的一粒弹珠。
•一张桌子,最好铺上桌布,以便能标出目标点以及弹珠落下后静止的位置。
程序
首先在桌布上标出一点作为目标。
规则1 将漏斗口对准目标点。保持这种状态,将弹珠由漏斗口落下50次,在弹珠每次静止的位置作记号。
规则1的结果令人失望(图26.1)。我们得到近似圆形的轨迹,范围远大于我们的预期。虽然漏斗口一直都是对准目标点,但是弹珠似乎会滚到任何方向,有时很靠近目标点,下一次又落在目标点东北30厘米处,再下次则落在目标点西南15厘米处。
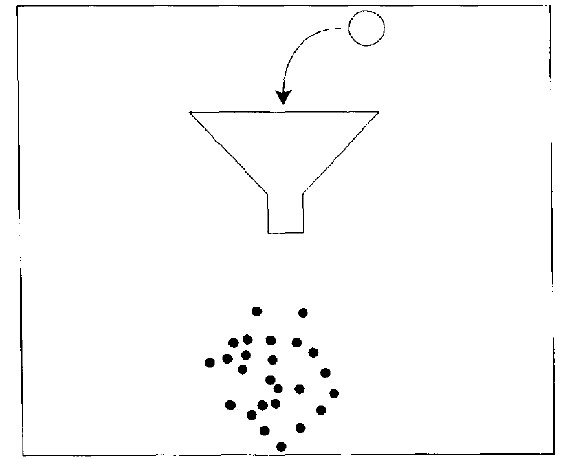
图26.1 按规则1投掷弹珠的记录
我们一定可以做得更好。为什么不在每次弹珠落下后,调整漏斗的位置,让下一次的结果靠近目标点?因此我们定出了规则2。
规则2 根据每次弹珠落下后的静止位置与目标位置的差距,将漏斗由现有的位置移动,以弥补前次的偏误。例如弹珠停在目标点东北30厘米处,则将漏斗由现在位置往西南移30厘米。
结果再次令人失望,这次得到的结果比规则1的结果还糟(图26.2)。假设偏误可能发生在任何方向,那么依规则2的落点所形成的圆形,其直径的变异数,比依规则1直径的变异数还大一倍。因此,依据规则2所形成的概略圆形的直径比依据规则1所得的结果大41%。
既然成效不佳,再试定另一个规则吧。
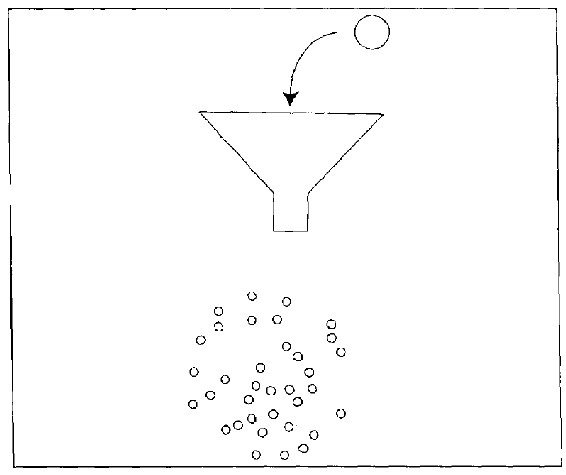
图26.2 按规则2投掷弹珠的记录
规则3 每次于弹珠落下后调整漏斗位置,但以目标点作为移动的参考点。按照落点与目标点的差距,把漏斗移往与目标点等距但相反方向的位置,以弥补前次偏误。
结果更糟(图26.3)。弹珠的落点来回移动,幅度愈来愈大,只有几次是幅度渐减,其后幅度又恢复愈来愈大。
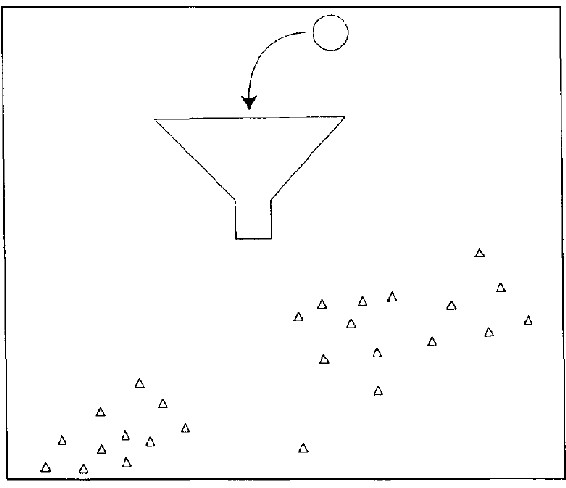
图26.3 按规则3投掷弹珠的记录
失望之余,我们不再尝试要建立一个优于规则1的规则,现在只求达到一致性,而不一定等于目标值,为此我们建立规则4。
规则4 在每次弹珠落下之后,就将漏斗移至该静止点之上。
结果更是令人失望。弹珠的落点逐渐走向云深不知处(图26.4)。
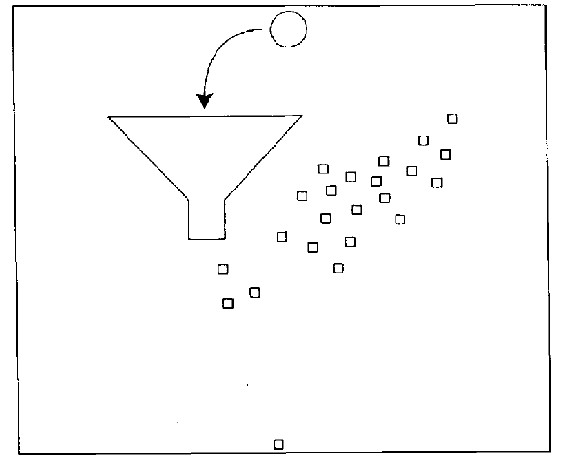
图26.4 按规则4投掷弹珠的记录
科罗拉多大学的皮腾堡(William Pietenpol)教授于1924年所描述的一个例子,可以用来诠释规则4。当时我是他的学生,正在修物理与数学硕士。
有个人醉得不辨东南西北,却仍希望走路回家。他走了几步,步履踉跄,站直了身体又走了几步,也搞不清东南西北;又走了几步,还是跌跌撞撞。如果这样乱走下去,他走得愈久,能够回到家的希望愈渺茫。
结论
规则1是所有规则中效果最好的。我们对规则1不满,因而制定了规则2、3、4,但结果却是愈来愈差。
因此我们应采取行动,并不是另行制定规则,而是设法改善规则1的结果。以下就是两项建议:
•降低漏斗的高度。效果很好,落点构成的近似圆形半径缩小。这样做的成本是多少答案是不费分文。
•改用比较粗糙的桌布。无论采用上述4种规则中的哪一种,弹珠滚动的距离都会缩短。成本多少?11美元便可以了。
属于规则2的干扰实例
有个人的工作是将铜溶液灌入一个模型中,铸出热气腾腾的铜块,每块重326公斤。每次自动称重的结果,会以斗大的数字出现在他的眼前。如果重量低于326公斤,他就以反时针方向调整操纵杆,超过326公斤,他就以顺时针方向调整操纵杆。
他的目的是让每块铜块的重量都一致。可惜这位仁兄与他老板都不知道,他的工作却造成适得其反的结果。他是在应用规则2。他领薪水所做的事,竟然是让结果更坏。
他应该如何做?很简单。把每次产出的铜块重量,一一点绘在纸上,然后观察它的趋势,观察是否持续在326公斤之上或之下。另一个更好的做法,就是为重量的平均数与全距(range)绘制控制图,例如每次将连续4块的值作为一小组,然后计算每一小组的平均数和全距,再画出管制上限与下限,观察各点在控制图上的分布情形。如果有超出控制界限的点,追究其特殊原因并设法去除,以免再次发生。如果平均数控制图的中心线与设定的标准重量相差很多,可能就需要调整重量的水准。另一方面,思考一下原先设定的重量是否合理?这必须要看铜块预定的用途而定。
以下是规则2的另一些干扰实例:
•某些依据回馈而作调整的机制。
•只要一件产品不合规格就调整生产过程。
•工人常用的调整方式。
•为了目前的产出而调整工作标准。
•美国联邦和州的立法对经济的干预。
•美国联邦储备局(Federal Reserve Board)调整利率的方式。
•由于单一顾客的抱怨而做出反应。(当然,让顾客高兴应不计代价。)
•证券市场对消息的反应。
•对谣言的反应。
•如果本批的基本原料浓度需要提高20%,便修改规格,将浓度提高20%。
•依照上一版本的设计进行工程变更,而未参照原始的构想。
•主管开工前,依据昨日的绩效重新设定生产过程。
•依据最新的顾客态度调查而改变公司政策。
•当乳酪太咸时,冲淡制乳酪的卤水;而当乳酪不够咸,便在卤水中加盐。
•持续修改税法,每次改变都是想修改前次的错误。
•持续改变医疗给付水准,每次改变都是想修改前次的错误。
•价格战。甲公司大幅降低汽车售价,竞争对手将价格降得更低;接着甲公司再降低价格,其他公司也再次跟着降价。价格战何时停止?谁是赢家?也许有某些顾客获利,但社会整体会有损失,因为所有公司将资金都投入在折价战中,而没有钱从事研究和改善了。
还有一个近似规则2的例子:月底时,我们有一些原料没有用完,因此在下一个月就少订一些原料。反之,如果本月底发现原料不足,就改采取相反的做法。我们对于经费也是如此处理,即依据前一年的状况,来调整本年度的预算。
这算是规则2的例子吗?或许是。但是如果剩余或不足是由于经济的萧条或景气,那么前述的反应或许是错的,或许有部分是错的。问题是,一个月的剩余或不足,到底有多少是来自经济状况持续恶化或好转的呢?
属于规则3的干扰实例
•核扩散。
•贸易壁垒。
•毒品走私。政府加强查禁,促使毒品存量减少,结果市场上毒品的价格上涨。较高的售价刺激毒品走私进口,于是政府更加强查禁。
这个循环持续不断地进行,而且问题愈来愈严重,不知该如何是好?依据《哈拍》杂志的统计:美国每年查获与没收毒品的平均金额:
每位稽查员 124,000美元
每条缉毒犬 3,640,000美元
(解决办法:引进更多缉毒犬)
•将赌金加高,希望能把输掉的钱补回来。
属于规则4的干优实例
•语言的演化。实例:拉丁语系(意大利语、法语、西班牙语、葡萄牙语)彼此之间的差异,以及它们与原始拉丁语的差异。
•未经文字记录而代代相传的历史。
•聚集一堂,交换看法(没有外力帮助)。
•民播。
•工人一个接一个训练新手。
我问一位女士,你是如何学会你的工作的?她回答说,强哥、莉妹、阿美,这些同样职位的工人教我的。工作过不多久,她就帮忙训练新手。之后,这位新手又去教别的新手。
当然,实际在现场工作的人,确实对工作比较熟悉。但是连续由一位工人教导下一位新工人的方式,却可能会造成工作方法愈来愈离谱。比较好的做法是,指定一位工人负责训练,最好能挑选一位熟悉工作又擅长教学的人。
•交响乐团的演奏者一位接一位,依序为乐器调音,而不是依相同音源来调音。
•主管集会,商讨面对新经济时代该做些什么。
•依据前一批货搭配颜色。
•根据上一次会议实际开始的时间,调整本次赴会的时间。
•有样学样。在毫无理论基础下向范例学习。
•贴壁纸。
•生活成本的调整(COLA,cost of living adjustment)。工资依据生活成本调整,生活成本又依据工资调整。
•利用上一版的剪裁作为下一版的样版。
•玩“打电话”(telephone)或称“邮局”(post office)游戏。8个或8个以上的人围成一圈,其中某个人向坐在邻座的人轻声讲一个短句,这个人再把这句话传给隔壁的人,如此传一圈后,原来的那句话会变得如何?当然是愈来愈走样!
一步一步求改善
一个稳定的过程,就是没有出现变异的特殊原因;而依据休哈特的说法,就是所欲测量的特性处于统计控制状态。它是一个随机过程,在近期内的行为可以预测。当然,也有可能发生某种不可预见的变动,而使该过程脱离统计控制状态。惟有过程在统计控制状态时,才具有一个可界定的性质。
假如你经过一番努力,使过程达到了管制状态,那就表示,你已针对超出控制界限的各点,设法逐一找出了特殊原因。此外,即使是在控制界限之内,当各点出现某些形态时,也可能代表有特殊原因存在,你也必须尝试找出该特殊原因,并且设法将之消除。
一旦已经达到统计控制,下一个困难的问题方才开始——改进系统。改进通常就是指降低变异(缩小控制界限),有时可能还需要把平均值(中心线)移至较高或较低的水准。如果想要改进一个稳定的过程,必须对该过程进行基本的改变。这种基本的改变有时候非常简单,例如,改善室内的照明。但有时候可能很复杂,甚至所费不菲,需要更高的授权与更多的努力。例如,增进客户与供应商双方高层管理者之间的了解。
如果一个系统并不值得花钱改善,那么不如转移心力到其他更值得注意的系统。我们在第27章会利用损失函数,研究缩小变异的效果。
即使是稳定的流程,仍可能会产出不合格品或发生错误,如果一有这种情况,就对流程采取行动,也就是干预该流程。任意干预的后果,只不过是增加未来的不合格品或错误,同时也增加成本——结果与我们想要达到的目的正好相反。
例如在红珠实验中,如果我们在红珠数目过高或过低时停止生产,试图去找出原因,就是一种干预。装置使产品符合规格的辅助工具,也是干预,只是徒然增加成本。
追溯过程的源头,乃是找出缺陷与错误的重要着力点。缺陷来自何处?其起因是什么?
特殊原因或许并不会再次发生。例如,瓦斯燃烧器的温度过高,损毁了价值5万美元的泡沫橡胶。根据一连串线索追踪的结果,发现原因是地下瓦斯的质量出乎意料的好。这时没有必要采取任何行动,因为这种情况在数十年内不会再发生。同时,顾客也很难采取什么措施,来确保将来不会再发生同样的问题。
另一方面,特殊原因或许会再发生。如果这样,除非所需经费过于庞大,否则应采取行动,防范再发生。假如变成周期性(如每周一早上10点)的再发生,则来源的线索就很明确了。如果再发生的情况属偶发性,就需要经过一番侦测才能找到源头。
最后,为了要以实际数字说明漏斗实验的各项规则,我们不妨把先前的红珠实验中,工人每次取得的红珠数拿来作为范例。假设以红珠数的平均值(9粒)当做目标值,如此一来,可将9粒红珠转换为0;7粒红珠转换为-2;11粒红珠转为2。在4项规则下,第一次投掷都是对准目标,而第一次投掷的结果也都相同。举例来说,在规则1下,漏斗每次投掷都是对准目标值。我们可以将结果计算如表26.1,并以图26.5表示它。
表26.1 依据漏斗实验各项规则而将图7.3红珠实验数据转换的结果
| 投掷 | 规则1 | 规则2 | 规则3 | 规则4 | ||||
| 次数 | 漏斗位置 | 结果 | 漏斗位置 | 结果 | 漏斗位置 | 结果 | 漏斗位置 | 结果 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | -3 | 0 | -3 | 0 | -3 | 0 | -3 |
| 3 | 0 | 3 | 3 | 6 | 3 | 6 | -3 | 0 |
| 4 | 0 | 2 | -3 | -1 | -6 | -4 | 0 | 2 |
| 5 | 0 | 5 | -2 | 3 | 4 | 9 | 2 | 7 |
| 6 | 0 | -5 | -5 | -10 | -9 | -14 | 7 | 2 |
| 7 | 0 | 2 | 5 | 7 | 14 | 16 | 2 | 4 |
| 8 | 0 | 2 | -2 | 0 | -16 | -14 | 4 | 6 |
| 9 | 0 | -2 | -2 | 4 | 14 | 12 | 6 | 4 |
| 10 | 0 | 1 | 2 | 3 | -12 | -11 | 4 | 5 |
| 11 | 0 | -1 | -1 | -2 | 11 | 10 | 5 | 4 |
| 12 | 0 | 2 | 1 | 3 | -10 | -8 | 4 | 6 |
| 13 | 0 | -2 | -2 | -4 | 8 | 6 | 6 | 4 |
| 14 | 0 | 2 | 2 | 4 | -6 | -4 | 4 | 6 |
| 15 | 0 | -4 | -2 | -6 | 4 | 0 | 6 | 2 |
| 16 | 0 | 4 | 4 | 8 | 0 | 4 | 2 | 6 |
| 17 | 0 | 0 | -4- | 4 | -4 | -4 | 6 | 6 |
| 18 | 0 | 3 | 0 | 3 | 4 | 7 | 6 | 9 |
| 19 | 0- | 1 | -3~ | 4 | -7 | -8 | 9 | 8 |
| 20 | 0 | 0 | 1 | 1 | 8 | 8 | 8 | 8 |
| 21 | 0- | 4 | 0- | 4 | -8 | -12 | 8 | 4 |
| 22 | 0 | 0 | 4 | 4 | 12 | 12 | 4 | 4 |
| 23 | 0 | 2 | 0 | 2 | -12 | -10 | 4 | 6 |
| 24 | 0 | 3 | -2 | 1 | 10 | 13 | 6 | 9 |
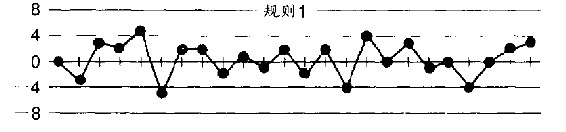
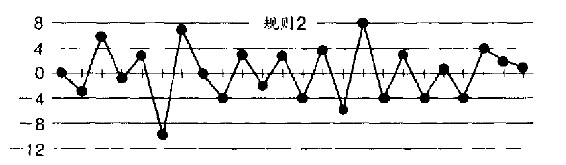
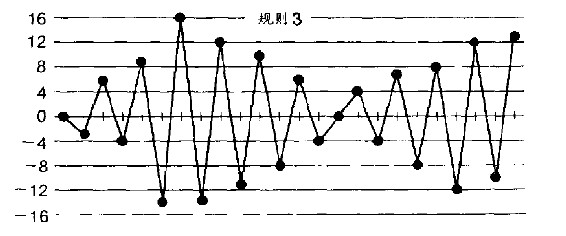

图26.5 依据表26.1结果栏数据所绘制的图
