分词
考虑中文文本“浮法像蝴蝶”,它的英语翻译是“float like a butterfly”。它包含5个字符,但是字符间没有空格,因此中文阅读者需要执行分词:决定单词的边界位置。英语阅读者通常不需要执行分词,因为单词间存在空格。但是,一些文本,如URL,通常不包含空格,但是有时输入错误,会留个空格;搜索引擎或文本处理程序如何纠正这样的错误呢?
比如英语文本“choosespain.com”,这是个网站,希望你选择西班牙作为旅行终点站。但是如果你把名字切分错误,你会得到这样的分词“chooses pain”,这个名字就不那么吸引人了。人工阅读可以通过几年的经验来做出正确的决策;但是把这种经验编码为计算机算法将是一项难以完成的任务。但是我们可以采取一种捷径,其效率之好让人惊讶:在二元表里查询每个词汇。我们发现“choose Spain”出现了3210次,而“chooses pain”在表里一次都没有出现(这意味着它在1MB的语料库中出现次数少于40次)。因此,“choose Spain”出现至少80次,可以作为正确的分割。
假如我们需要解释短语“insufficientnumbers”的含义,如果我们把单词的大小写加起来,其计数是:
insufficient numbers 20751 in sufficient numbers 32378
“In sufficient numbers”的出现频率高于“insufficient numbers”,但是这并不具备很强的说服力。这种情况令人沮丧:我们可以猜测,但是无法确定。对于类似这种不确定问题,没有方法能够确定地给出正确的值,我们还没有能够确保答案正确的完备模型,实际上人类专家也没有一个完备的模型,可以不同意该答案。但是,解决不确定问题有个确定的解决方案。
1.定义概率模型。我们无法定义所有的因子(语义的、语法的、词汇的和社会的)使得选择“choose Spain”对于一个域名是一个更佳的候选。但是我们可以定义一个简化的模型,从而能得到近似概率。对于“choose Spain”这种简短的候选,我们可以在语料库数据中查找n元,并使用该概率。对于更长的候选,我们需要切分为多个部分,组合这些部分得到结果值。核心是我们定义语言模型——在该语言中所有字符串的概率分布——从语料库数据中学习该模型参数,然后使用该模型来定义每个候选的概率。
2.枚举候选项。我们无法确定“insufficient numbers”还是“in sufficient numbers”更可能是所期望的短语,但是我们可以确定它们都是候选分割,如“in suffi cient numb ers”也是候选项,但“hello world”不是有效的候选项。在该步骤中,我们不做判断,只是枚举可能的候选项——如果可以,列出所有的候选项,或者列出仔细选择的一个样本。
3.选择最可能的候选项。对每个候选项应用语言模型来获得它的概率,选择概率最高的是选项。
如果你更习惯于数学等式表达,如下所示:
best=argmaxc∈candidates P(c)
或者,如果你更习惯于计算机代码表达,则如下:
best=max(c in candidates,key=P)
我们把这种方法用于分割中。定义一个函数、分段,把不包含空格的字符串作为输入,返回最佳分段的单词列表。
>>>segment('choosespain') ['choose','spain']
我们从步骤1——概率语言模型开始。单词序列的概率是每个单词概率的乘积,假设单词的上下文是:所有上述单词。等式表达如下:
P(W1:n)=Πk=1:nP(Wk|W1:k-1)
我们没有数据来精确地计算该等式。因此我们可以使用一个更小的上下文来近似计算。由于数据序列大于五元,我们就采用五元文法模型,因此N元文法的概率即给定前缀四个单词(不是前缀所有单词)的每个单词的乘积。
五元文法模型存在三个难题。第一,五元数据大约30G,因此无法全部装载到内存中。第二,很多五元计数将为0,我们需要一些回退(bcking off)策略,使用更短的序列来估计五元文法的概率。第三,候选项的搜索空间将会很大,因为依赖性扩展到四个单词。这三个难题花些时间都是可控的。但是,我们首先来考虑解决这三个问题的一个更简单的语言模型:一元模型,其序列概率即每个单词自身的概率乘积。在一元模型中,每个单词的概率和其他单词无关。
P(W1:n)=Πk=1:nP(Wk)
对'wheninrome'进行分割,考虑这些候选项,如when in rome,然后计算P(when)×P(in)×P(rome)。如果该候选项的乘积高于任何其他候选项,那么它就是最佳答案。
n个字符的字符串包含2n-1个不同的分割方式(字符间有n-1个位置,每个位置都可以作为分割边界)。因此,字符串'wheninthecourseofhumaneventsitbecomesnecessary'包含35T的分割方式。但是我确定你可以在几秒钟内找到合适的分割方式;显然,你不可能枚举所有的候选类型。你可能浏览了“w”、“wh”和“whe”,并作为不可能的单词放弃它们,而接受“when”作为可能的分割方式。然后继续剩余部分,并找到它们的最佳分段方式。一旦我们简化假设每个单词和其他的单词是不一样的,那意味着我们不需要考虑单词的所有组合。
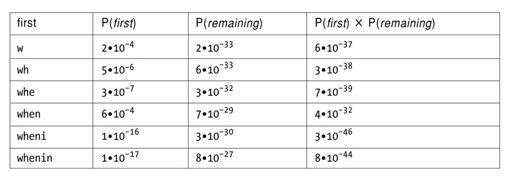
以上简单地给我们描述了segment函数:考虑把文本划分为一个起始单词和剩余文本的所有方式(可以任意限制单词最大长度,如L=20个字母)。对于每种可能的划分,找到对剩余文本分词的最佳方式。在所有的候选项中,乘积P(first)×P(remaining)值最高的即为最佳方案。
这里我们用一个表格来说明这个问题。表格中包含了第一个单词的所有候选、该单词的概率、剩余单词的最佳分词概率以及所有的概率(即第一个单词和剩余单词的概率的乘积)。我们发现,以“when”开始的分词概率是第二个最佳候选的5万倍。
我们可以通过几行Python代码来实现分词:
@memo def segment(text): "Return a list of words that is the best segmentation of text." if not text:return[] candidates=([first]+segment(rem)for first,rem in splits(text)) return max(candidates,key=Pwords) def splits(text,L=20): "Return a list of all possible(first,rem)pairs,len(first)<=L." return[(txt[:i+1],text[i+1:]) for i in range(min(len(text),L))] def Pwords(words): "The Naive Bayes probability of a sequence of words." return product(Pw(w)for win words)
这是整个程序——包含三个较小的省略部分:product是把数字列表进行乘积的工具函数;memo是一个装饰器(dcorator),对函数product的结果进行缓存,因而这些结果就不需要重新计算;Pw通过询问单元计数数据来估计一个单词的概率。
没有装饰器memo,对一个包含了n个字符的文本段的调用会导致对该段的2n次递归调用;有了memo,它就只执行n次调用——memo使得调用变成一个高效的动态编程算法。对于n次调用,每个都需要考虑O(L)次的分片,对每个分片乘以O(n)的概率来估算每个分片的代价,因此整个算法代价是O(n2L)。
对于P w,我们从一个数据文件读取单元计数值。如果一个单词在语料库中出现,它的估计概率是Count(word)/N,其中N是语料库的大小。实际上,我没有采用1300万类型的单元数据文件,而是创建了vocab_common,它有几方面特性:(1)大小写不敏感,因此“the”、“The”和“THE”的计数值都加在一起,作为一个词条的“the”;(2)词条是由字母表示的,而不是数字或者标点符号(因此“+170.002”不能作为词条,同样“can't”也不能;(3)100万单词中最通用的1/3单词。
Pw唯一较难处理的部分是当一个单词不在语料库中时如何处理更为合适。即使是在包含了10000亿个单词的语料库中,这种情况有时也会发生,因此把概率当做0返回是错误的。但是它应该为多少呢?语料库中的token个数N,几乎有10000亿,vocab_common中最不经常出现单词有12711个。因此之前没有看见的单词,其概率应该在0~12711/N。不是所有未见到的单词的概率都是一样的:一个有20个字母的随机序列是单词的概率要小于一个有6个字母的随机序列。我们将为概率分布定义一个类Pdist,它加载一个内容是(ky,count)对的数据文件。默认情况下,一个未知单词的概率是1/N,但是Pdist的每个实例可以提供一个自定义函数对默认值进行重载(oerride)。为了避免对于很长的单词概率太高,因此我们确定(相当随意)了一个起始概率10/N,对于候选单词中的每个字母,以因子10来递减。我们定义Pw为一个如下的Pdist:
class Pdist(dict): "A probability distribution estimated from counts in datafile." definit(slf,data,N=None,missingfn=None): for key,count in data: self[key]=self.get(key,0)+int(count) self.N=float(N or sum(self.itervalues())) self.missingfn=missingfn or(lambda k,N:1./N) defcall(slf,key): if key in self:return self[key]/self.N else:return self.missingfn(key,self.N) def datafile(name,sep='\t'): "Read key,value pairs from file." for line in file(name): yield line.split(sep) def avoid_long_words(word,N): "Estimate the probability of an unknown word." return 10./(N10*len(word)) N=1024908267229##Number of tokens in corpus Pw=Pdist(datafile('vocab_common'),N,avoid_long_words))
注意,Pw[w]是单词w的原始计数,而Pw(w)是它的概率。本章描述的所有程序都能够通过http://norvig.com/ngrams获得。
因此,该模型分割的效果如何呢?以下是一些实例:
>>>segment('choosespain') ['choose','spain'] >>>segment('thisisatest') ['this','is','a','test'] >>>segment('wheninthecourseofhumaneventsitbecomesnecessary') ['when','in','the','course','of','human','events','it','becomes','necessary'] >>>segment('whorepresents') ['who','represents'] >>>segment('expertsexchange') ['experts','exchange'] >>>segment('speedofart') ['speed','of','art'] >>>segment('nowisthetimeforallgood') ['now','is','the','time','for','all','good'] >>>segment('itisatruthuniversallyacknowledged') ['it','is','a','truth','universally','acknowledged'] >>>segment('itwasabrightcolddayinaprilandtheclockswerestrikingthirteen') ['it','was','a','bright','cold','day','in','april','and','the','clocks', 'were','striking','thirteen'] >>>segment('itwasthebestoftimesitwastheworstoftimesitwastheageofwisdomitwastheage offoolishness') ['it','was','the','best','of','times','it','was','the','worst','of','times', 'it','was','the','age','of','wisdom','it','was','the','age','of', 'foolishness'] >>>segment('asgregorsamsaawokeonemorningfromuneasydreamshefoundhimselftransformed inhisbedintoagiganticinsect') ['as','gregor','samsa','awoke','one','morning','from','uneasy','dreams','he', 'found','himself','transformed','in','his','bed','into','a','gigantic', 'insect'] >>>segment('inaholeinthegroundtherelivedahobbitnotanastydirtywetholefilledwiththe endsofwormsandanoozysmellnoryetadrybaresandyholewithnothinginittositdownonortoeat itwasahobbitholeandthatmeanscomfort') ['in','a','hole','in','the','ground','there','lived','a','hobbit','not','a', 'nasty','dirty','wet','hole','filled','with','the','ends','of','worms','and', 'an','oozy','smell','nor','yet','a','dry','bare','sandy','hole','with', 'nothing','in','it','to','sitdown','on','or','to','eat','it','was','a', 'hobbit','hole','and','that','means','comfort'] >>>segment('faroutintheunchartedbackwatersoftheunfashionableendofthewesternspiral armofthegalaxyliesasmallunregardedyellowsun') ['far','out','in','the','uncharted','backwaters','of','the','unfashionable', 'end','of','the','western','spiral','arm','of','the','galaxy','lies','a', 'small','un','regarded','yellow','sun']
看到程序正确地对一些生僻的单词如“Samsa”和“oozy”进行分割,你可能会很高兴。对于“Samsa”在10000亿个单词中出现了42000次,“oozy”出现了13000次,你应该不会太惊讶。分割的整体结果看起来不错,但是有两个错误:'un'、'regarded'应该是一个单词,而'sitdown'应该是两个单词。尽管如此,分词的准确率是157/159=98.7%,还是不错的。
第一个错误是由于“unregarded”在我们的三十多万单词的词汇里(它在所有单词词汇中的位置是1005493,计数值是7557)。如果我们把它放入词汇中,我们发现之前的分词是正确的。
>>>Pw['unregarded']=7557 >>>segment('faroutintheunchartedbackwatersoftheunfashionableendofthewesternspiral armofthegalaxyliesasmallunregardedyellowsun') ['far','out','in','the','uncharted','backwaters','of','the','unfashionable','end','of','the','western','spiral','arm','of','the','galaxy','lies','a','small','unregarded','yellow','sun']
这并没有证明我们解决了问题:我们需要放回所有其他的干扰单词,而不仅仅是我们需要的那个;而且我们需要返回所有的测试案例,确保增加其他的单词并没有混淆了任何其他的结果。
第二个错误是虽然“sit”和“down”是频繁词(概率分别为0.003%和0.04%),但是这两个单词的概率乘积刚好略小于“sitdown”这个单词本身的概率。根据二元计数,两个单词序列“sit down”的概率比其分别的概率乘积约大100倍。我们可以通过对二元建模来解决这个问题;也就是说,考虑每个单词的概率,给定前一个单词的概率是:
P(W1:n)=Πk=1:nP(Wk|Wk-1)
当然,整个二元单词表无法全部装载到内存中。如果我们只保留出现100000次以上的二元单词,结果就有250000多的入口项,这也无法装载到内存中。然而,我们可以通过Count(sit down)/Count(sit)来估计概率P(down|sit)。如果一个二元单词在表中不出现,我们就通过单元值来计算。在一个单词的前序单词给定的情况下,我们可以定义这个单词的条件概率cPw如下:
def cPw(word,prev): "The conditional probability P(word|previous-word)." try: return P2w[prev+''+word]/float(Pw[prev]) except KeyError: return Pw(word) P2w=Pdist(datafile('count2w'),N)
(细心的人会注意到cPw不是概率分布,因为对于一个给定的先验单词,所有单词的概率之和会超过1。这种方法的技术名称是“愚蠢回退”(supid backoff),但其实际效果很不错,因此我们不用担心。)我们现在来比较包含先验单词“to”、“sitdown”和“sit down”的概率:
>>>cPw('sit','to')*cPw('down','sit')/cPw('sitdown','to') 1698.0002330199263
我们发现“sit down”比“sitdown”的概率高1698倍,因为“sit down”是一个高频的二元项,而且“to sit”词频很高,而“to sitdown”词频不高。
这看起来振奋人心:让我们用二元模型来实现新版的分词。但要实现这种新版分词,我们还需要解决另外两个问题:
1.当给一个由n个单词构成的序列增加一个新的单词时,它调用Pwords来对这n+1个概率值进行乘法运算。但是分词时,原有的n个概率值已经做过一次运算处理了。将每个元素的运算结果也就是概率值保存起来,这样添加一个单词的时候就只需要另外执行一次运算,因此分词也将更为高效。
2.可能存在算术运算向下溢出问题。如果我们把Pwords应用于一个出现了61次“blah”之后的序列,我们将得到5.2×10-321的概率,而如果再加上一个“blah”,其概率为0.0。我们能够表示的最小正浮点数是4.9×10-324;任何小于该值的概率都置为0.0。为了避免向下溢出,最简单的解决方案是对这些数值使用对数运算而非直接进行乘法运算。
我们将定义“segment2”(分词2),它和分词有三个方面的区别:第一,它使用了条件二元语言模型,cPw,而不是单元模型Pw。第二,函数特征是不同的。“segment2”除了需要把“文本”作为一个参数传递给函数之外,还需要将这段文本的一个单词也传递给函数。在句子的开始,前一个单词是句子的起始标记<S>;其返回值也不只是一个单词的序列,而是包含了两项内容:分词的概率和单词序列。我们返回概率,这样可以把它保存起来(通过记录的装饰器memo),不需要重新计算;这解决了问题:(1)的效率低问题。合并函数接受四个输入:第一个单词、剩下的单词以及它们分别的概率。合并函数会把第一个单词添加到其他单词后面,并对所有的概率值进行乘法运算。但为了解决问题(2)[1]我们引入了第三个区别:不对概率值直接进行乘法运算而是对概率的对数执行加法运算。
以下“segment2”的代码:
from math import log10 @memo def segment2(txt,prev='<S>'): "Return(log P(words),words),where words is the best segmentation." if not text:return 0.0,[] candidates=[combine(log10(cw(first,prev)),first,segment2(rm,first)) for first,rem in splits(text)] return max(candidates) def combine(Pfirst,first,(Pem,rem)): "Combine first and rem results into one(probability,words)pair." return Pfirst+Prem,[first]+rem
segment2执行了O(nL)次的递归调用,每次调用需要考虑O(L)次的切分,因此整个算法的复杂度是O(nL2)。实际上,这就是Viterbi算法,memo隐含地创建Viterbi表。
segment2正确地对“sit down”例子进行分割,第一个版本中能正确切分的例子,在这个版本中也仍然是正确的。但这两个版本对“unregarded”的分词都不正确。
我们能否在性能上有所提升?很有可能。我们可以对未知单词创建一个更精确的模型;可以组合更多的数据,或者在单元数据或者二元数据中保留更多的入口项,或者添加三元数据。
[1]乘法运算的向下溢出问题。
