实例2：估计的时间序列

图19-2说明了经典的逻辑回归（一种预测“是/否”结果的标准统计方法）方法的一个问题，以及如何使用所谓的弱信息化的贝叶斯方法来解决该问题。对于从1952～2000年每次美国总统选举的投票数据，我们为每年的数据拟合了一个分离的逻辑回归模型，预测给定种族、收入和一些其他变量的共和党人的投票选择。

在每个小图中，每个点代表一个逻辑回归系数，垂直线条表示估计的不确定性程度。点序列显示了每种选择的单独的估计，图形中的两行显示了种族和收入的估计系数的时间序列。（为了简单起见，我们没有将其他的系数列在这里。）图中的最左边一列的两个图形使用的是经典的估计，而最右侧的两列则采用的是两种不同的贝叶斯估计（在这个例子中，它们生成的答案基本相同）。

图19-2的估计结果看起来不错，除了1964年是一个完全的分隔点，那一年所有的黑人都支持民主党。因此，种族系数的估计值是负无穷大——也就是说，其推论是那一年黑人选举共和党的概率是0%。1964年共和党确实不受黑人选民支持（那年共和党候选人是Barry Goldwater，他曾经反对《the Civil Rights Act》），因此他们得到的黑人选票肯定为0。这种回归的目的，正如几乎所有的调查分析一样，是为了得出关于普通人群的结论，而不仅仅是调查一个小样本，因此，我们不能仅仅满足于经典的负无穷大的估计结果。（图19-2左栏显示的估计实际上不是无限的，那是因为用于拟合模型的软件是迭代的，在达到一定程度之后就停止了。）

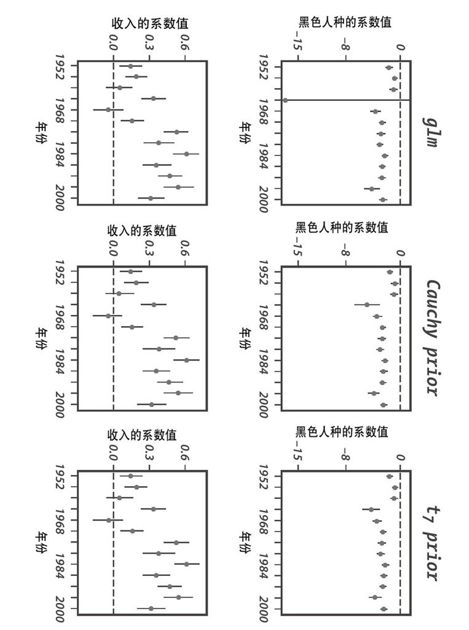
图　19-2：左栏显示了在一个逻辑回归中的两个预测器的估计的系数值（标准误差±1），预测共和党人会选举民主党候选人作为总统的概率，对美国选举研究中心提供的从1952～2000年的每次选举的数据进行分别拟合。数值变量收入（初始值规模是1-5）首先被集中起来，然后通过除以两种标准差重新调整规模。1964年存在一个完全分割点（没有一个非洲裔的选民支持共和党候选人Barry Goldwater)，导致那一年预测器的系数估计值为-1。（该估计的有限值和标准误差是通过多次使用统计建模工具R中的glm函数进行迭代确定的，直到程序终止。）其他两列显示了对于相同模型，使用不同的“弱信息”先验分布的贝叶斯估计。贝叶斯推论解决了1964年由于完全分割点导致的预测器系数估计值为-1的问题，而对其他年份的估计则没有太多效果

本图以及其他和它类似的图的优点在于，它的严格并行性（1990年Tufte和1967年Bertin提出的“小倍数”思想）允许读者——以及该图的创建者——一次性做出很多比较。

贝叶斯方法，正如图19-2的最右侧两栏所示，为1964年的黑人选民系数生成了一个合理的值——低于1952～2000年中的任何一年，而且有更大的不确定性边界，但不是无限的。在解决该问题时，贝叶斯程序并没有混合其他年份或者模型中的其他变量的系数估计（正如图中第二行的收入系数所示）。

该图谈不上漂亮，但是它说明了一条重要且通用的原则，即图形化不仅仅只是为原始数据做的。统计学中常见的实践是在一张表中显示这种结果，但是好的图形可以通过更少的空间显示更多的信息(Glman等2002）。

从我们的角度考虑，以图形的方式展示参数估计有助于向别人表达我们的方法的有效性，同时也可以进一步证实我们的估计序列是合理的，而将估计系数放到一个表格中的方式（或者更经典的计算机输出的很长的序列）将无法达到这种效果。