拼写纠正

我们的最后一个任务是拼写纠正：给定一个输入的单词w，确定单词c是其最可能要表达的单词。举个例子，如果w是“acomodation”，c应该是“accommodation”。（如果w是“the”，那么c也应该是“the”。）

根据标准的方法，我们想要选择c，使得其条件概率P(c|w）值最大。但是如何定义该概率却不简单。假设w=“thew”，那么c的一个候选项是“the”——它是最常见的单词，我们可以想象是打字员的手指输入“e”后不小心按到“w”。另一个候选项是“thaw”——一个较常见的单词（虽然出现概率比“the”低3万倍），而且用一个原因取代另一个很常见。其他的候选项包括“thew”本身（表示肌肉或者肌腱的模糊术语），“threw”和一种姓氏“Thwe”。我们应该选择哪一种？看起来我们合并了两种因素：c本身的概率是多大？w是c的输入错误，或者是拼读错误，或者是其他某种形式的误拼，它们的概率有多大？有人可能会认为我们将通过某种特殊(a hoc)方式来结合这些因素，但是实际上存在一个数学公式——贝叶斯理论——精确地告诉我们如何组合这些因素来找到最佳的候选项：

argmaxc P(c|w）=argmaxc P(w|c）P(c) 这里，P(c)表示c是期望的结果单词的概率，称为语言模型；P(w|c）表示用户期望获取c会输入w的概率，称为错误模型或者噪音渠道模型。（其想法是用户希望输入c，但是由于一些噪音或静态数据，改成了输入w。）遗憾的是，从我们拥有的语料数据来看，对该模型进行估计并不容易——语料库没有提供信息表示哪些单词是其他单词的拼写错误。

我们可以通过更多的数据来解决这个问题：一个错误拼写列表。Roger Mitton在http：//www.dcs.bbk.ac.uk/～ROGER/corpora.html维护了一个约1万条（c,w）词对的数据语料库。但是我们不能只是从该数据中查找P(w=thew|c=thaw)；若只有4万条例子，那么看到相同的词对的概率很低。当数据很稀疏时，需要对它进行范化。可以通过忽略相同的字母、“th”和“w”来进行范化，计算P(w=e|c=a），即期望输入字母“a”却输入“e”的概率。由于存在如“consistent/consistant”和“inseparable/inseperable”这样的错误，把“a”误拼写为“e”是最常见的一种单词误拼。

在以下表中，我们考虑当w=thew时，c的五个候选项。其中一个是thew本身，另外四个表示我们将要考虑的四种单步编辑类型：1）删除字母“thew”中的“w”，生成“the”。2）插入“r”，得到“threw”。以上两种编辑都是考虑编辑其前一个字母。3）用“a”替换“e”，如之前所述。4）对两个相邻字母交换位置，把“ew”交换成“we”。我们称这些单步编辑为编辑距离1；需要两步编辑的候选项是编辑距离2。下表显示单词w和c，编辑w|c，概率P(w|c），概率P(c)，以及二者概率的乘积（为了可读性进行了扩展）。

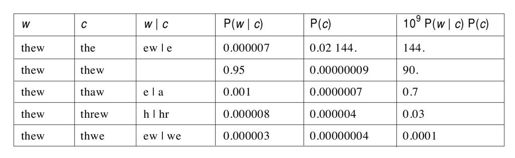
从表中可以看出，“the”是最可能的纠正结果。P(c)可以和Pw一起计算。对于P(w|c），我们需要创建一个新的函数Pedit，它给出了一步编辑操作的概率，从拼写错误的语料库中估计出来。举个例子，可以计算Pedit（'ew|e'）=0.000007。更复杂编辑定义成单步编辑的连接。例如，为了把“hallow”转换成“hello”，我们把a|e编辑操作和ow|o编辑操作连接起来，因此整个编辑被称为a|e+ow|o（或者ow|o+a|e，在这种情况下（但不总是如此）是相同的）。复杂编辑的概率等于其各个子部分的乘积。

存在一个问题：空编辑Pedit（''）的概率有多大？也就是说，假设期望的单词是c，人们真的输入c而不是其中某种错误的编辑？这依赖于打字员的熟练程度以及是否有检查。很随意地，我假定每20个单词出现一次拼写错误。值得注意的是，如果我假定每50个单词才出现一次错误，那么对于w=“thew”，P(w|c）的概率为0.98.，而不是0.95，而且“thew”将是最可能的结果。

最后，我们可以展示代码了。该代码包含两个高层函数correct和corrections,correct函数返回一个单词的最佳纠正，corrections函数把correct应用到文本中的每个单词，对其邻近字符不做改动。候选项是所有可能的编辑，而最佳候选项是有最高的P(w|c）P(c)分值的候选项。

候选项是通过编辑生成的，即传递一个单词，返回一个{单词：编辑}对的词典dict表示可能的纠正。通常来说，可能对于一个纠正存在多种编辑。（例如，我们通过在“e”或者“l”后面插入“l”后，都可以把“tel”转为“tell”。）我们选择有最高概率的编辑。edits是我们目前为止最复杂的函数。一部分原因是该函数本质上就很复杂，生成4种编辑很复杂。但是一部分是因为我们采取了一些措施使得该函数变得高效。（性能较低但是易于读取的一个版本在http：//norvig.com/spell-correct.html。）如果我们考虑所有的编辑，一个单词如“accommodations”可以生成233166个候选项。但是只有11种候选项可以在词汇库中找到。因此，编辑是通过预计算词汇库中所有单词的所有前缀才能工作。然后，它递归调用edits，把单词分成头部和尾部（代码中的hd和tl)，并保证头部总是在前缀列表中。通过把结果添加到词典库dict中进行收集：

以下是使用edits函数的一个例子：

以下是正在工作的拼写纠正器：

15个单词中有13个处理结果正确，但是“acommodations”和“mispellings”处理结果错误。为什么呢？遗憾的是，网络上充满了很多错误的拼写。错误的单词“mispellings”在语料库中出现了18543次，而正确的单词“misspellings”只出现了50万次，这其中的差距不足以带来用一次编辑替换无编辑。“thew”出现了96759次，我怀疑其中绝大多数也是由于拼写错误。

有很多种方式可以改进这个拼写程序。首先，我们可以通过上下文的其他单词来纠正这个单词，因此“they're”本身是正确的，但是当出现在“in they're words”时，就会被纠正为“their”。一个单词二元模型或者三元模型就可以实现它。

我们真的需要清洗语料库中的拼写错误。看看以下这些不同的“misspellings”：

语料库中使用的misspellings一词，拼写错误的概率达到了7%。可以有三种方式来解决这个问题。第一种，我们可以获得一个字典单词列表，并且只对字典中的单词纠正错误。但是字典没有列出最新发明的单词和名字。（一种折中方案是把单词变成小写放到字典词汇中，但是允许全部大写的单词不在字典库中。）第二种，我们可以获得一个已经仔细校验过的语料库，可能是来自于高品质的出版社的书籍和期刊。第三种，我们可以纠正语料库中的错误。在使用语料库进行拼写检查之前，先对语料库拼写检查，这看起来就像是“循环论证”(crcular reasoning)，但是可以实现。对于这个应用，我们把编辑距离很小的单词聚在一起。针对每组相似单词，我们检查是否有某个单词的出现频率要远远高于其他单词。如果存在这个单词，我们将检查二元模型（或者三元模型）计数来观察这两个单词和相邻的单词是否有相似的分布。例如，以下是“mispellings”和“misspellings”的四个二元文法模型计数：

这两个单词共享很多相同的二元文法相邻的单词，对于这些单词组合中，总是“misspellings”的出现频率更高，因此很有可能“mispellings”是拼写错误。初级测试表示这种方法效果不错——但是存在一个问题：它需要CPU计算好几百个小时。因此，这种方法适合于在一个工作组上执行计算，而不适合于单机。

这种数据驱动的方法与更传统的软件开发过程相比如何？对于后者，程序员在编码中制定了一些显示规则。为了回答这个问题，我们一起来看ht：//Dig项目的拼写纠正代码，Dig是一款优秀的开源企业内网搜索引擎。给定一个单词，ht：//Dig项目的metaphone算法可以生成一个关键字来表示这个词的发声。举个例子，“tough”和“tuff”都映射到关键字“TF”，因此可以作为互相拼写错误的候选。以下是对于字母“G”的metaphone算法的代码：

/*

*/

这块代码正确地把“TOUGH”中的“GH”映射为“F”，但是不会把“BOUGH”中的“GH”映射为“F”。但是这些规则是否正确地捕获了所有的情况？“OUGHT”呢？或者“COUGH”和“HICCOUGH”？我们可以编写测试样例来验证代码的每个分支，但是即使如此，我们还是无法知道哪些方面没有覆盖全。当引入新的单词如“iPhone”，结果会如何呢？显然，手工制定的规则很难扩展和维护。数据驱动方法的很大优势是在数据中包含了很多信息，可以简单地通过增加更多的数据来增加新的知识。另一个优点是，虽然数据是海量的，但代码却很简洁——函数correct只包含50行左右的代码，而ht：//Dig的拼写代码超过1500行。正如伟大的Bill Gate所言：“通过代码行数来衡量编程进展正如通过重量来衡量飞机建造过程。”Gates认为代码行数是一种负担，而不是财富。概率性的数据驱动方法是敏捷开发的终极。

该算法的另一个问题是可移植性。如果我们想要一个拉脱维亚语(Ltvian)的拼写纠正器，该英语metaphone规则几乎毫无用处。把数据驱动的纠正算法移植到另一种语言上，我们需要的是一个大的拉脱维亚语的语料库，而不需要改动代码。