观察标签
除了所有顺序和数值的数据,我们包含一组自由格式的标签,用户能够输入人的照片。标签范围从描述性的(“雀斑”、“鼻子带环”)到粗俗的(“抱我上床吧”、“肮脏的胸口”)到友好的(“你穿着红色的衣服很漂亮”)到建议性的(“修修头发”、“避免在太阳下暴晒”)到评论性的(“太让人惊叹了!”、“Nancy,够了!”)到卑鄙的(“那个肥胖的朋友”)到没有意义的(“……”、“plokmnjiuhbygvt fcrdxeszwaq”)。通常来说,自由格式的文本数据处理上更复杂。第一件要做的事是检查标签的分布。最常见的标签是什么?
Load our tags >face_tags=read.delim("face_tags.tsv",sep="\t",as.is=T) then count >counts=table(face_tags$tag) and rank them. >sorted_counts=sort(counts,decreasing=T) Show the most common tags. >sorted_counts[1:20]
以下表包含了输出结果。
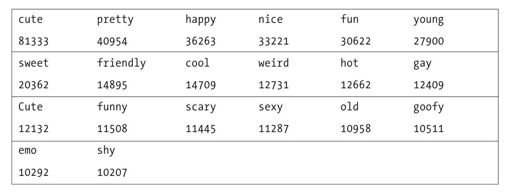
最不常见的标签是什么?
Show the least common tags. >tail(sorted_count,20)

查看一些标签会对范化有问题。“cute”和“Cute”是否应该归并为相同的标签?标点符号是否应该全部丢掉?看起来很滑稽的亚洲字体的全角问号(?)是否应该认为和ASCII的问号(?)一样?显然,这取决于应用。只要可能,我们的本能是慎之又慎,保留原始数据的完整性。这保护了信息;举个例子,标签“hot”和“HOT!”肯定包含不同的语义内容。通常,当针对特定的可视化或者分析,对数据进行归并是更容易的,而不是提前猜测所有的需求,并且被强迫撤销所有值钱的范化决策。
标签分布的基本绘图查看的是标签的频率相对于其频率的排序。通常来说,当对单词或者其他词汇项进行计数时,我们看到的是从最频繁出现的单词很快下降到最不频繁出现的单词。在我们的数据,总共有240万的标签,其中有29万个唯一标签。最高的1000个唯一标签出现频率是140万——超过所有标签的一半。而在这些标签的出现频率中,有非常显著的下降趋势。从常用标签表中,我们看到最常见的标签“cute”出现了3.6万次,而第二常见的标签“pretty”出现的频率只有它的一半。
For the top 1,000 tags, >s=sorted_counts[1:1000] draw a plot of their counts. >barplot(s)
1935年,语言学家George Zipf观察到词频分布遵循“幂函数定律”(pwer law),其中第n个单词的频率和(1/ns)成正比,其中s是个常量。和高斯分布不同,该分布包含有限的变量,这使得它不适合于某些统计算法。流行的书如Nassim Nicholas Taleb的《The Black Swan》(Rndom House出版)和Chris Anderson的《The Long Tail》(Hperion出版)使得这些分布分别以“重尾”和“长尾”分布而著名。实际上,我们的数据包含一条很长的长尾:22万个单词,或者词汇的76%只出现一次。
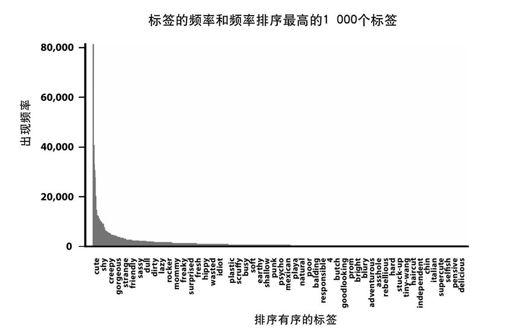
图 17-10:出现频率最高的1000个标签的标签频率
通过在对数空间描绘我们的单词的出现频率图,我们可以查看这些单词出现的频率是否满足幂函数定律分布(见图17-11):
Plot log ranks >log_ranks=log(1:length(sorted_counts)) against log frequency. >plot(log_ranks,log(sorted_counts))
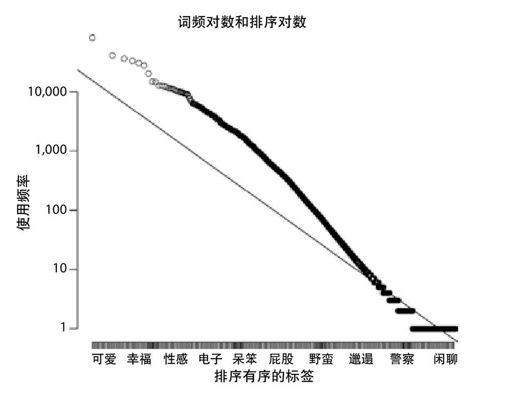
图 17-11:通过对数排序的标签的对数频率,包含幂函数定律模型的拟合线
幂函数定律分布在对数-对数空间上,看起来应该是线性的:
Fit a model of log count against log rank >model=lm(log(sorted_counts)~log_ranks) and draw it on Figure 17-10. >abline(model)
我们发现标签的概率很接近(1/n80)分布。(如果你觉得它看起来像最佳拟合线,记住所有点的76%是在数据的最右下侧的边上)
如果你在任何文本——报纸、小说、Web页面等上描绘这种对数-对数频率的绘图——它看起来都很相似[1]。当然,当FaceStat的用户写描述标签时,它们参与的是一种语言行为,这种行为和其他类型的人类通信在本质上很相似。
这些标签如何拟合剩余的数据?第一步需要做的是从标签中随机选取样本,在我们已经生成的绘图上绘制(见图17-12)。
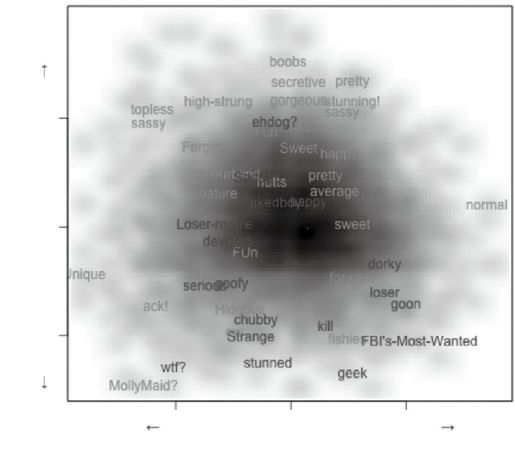
图 17-12:基于平滑后的魅力与年龄描绘的标签样本图(见彩图64)
在该图中,深暗色表示政治背景和魅力的密度的全局分布。单词是从分布中随机抽样出来的。蓝色词表示男性标签,粉色词表示女性标签。这么做可以使我们感觉到标签是否和图中的变量一致。数据看起来很合理,标签“平均”显示在图形的中央,而被标记为“接近顶尖”的人显示在“自由/魅力”象限,而标记为“土里土气的”则是在“保守/丑陋”象限。该图可以通过不同的随机种子生成多次,可以查看全局数据的标签分布。
[1]Zipf,George.1935.《The Psychobiology of Language》(MT出版社)参见http://en.wikipedia.org/wiki/Zipf's_law。
