年龄、魅力和性别
我们想要放大一些观察到的最有趣的属性:年龄、性别和魅力。每当我们用一个表来包含一些有趣的字段,把数据作为一个散点图展现出来通常是非常直观且信息量丰富(见图17-5):
Draw a scatterplot of age vs.attractiveness,>plot(d$age,d$attractive, using gender to define the points'colors.col=ifelse(d$male,'blue','deeppink'))
该散点图包含提示作用。举个例子,女人似乎比男人更有魅力。但是很难对任何事情有一个确定的答案,因为成千上万的点描绘时互相交叠在一起。当数据过载时,散点图可能会有误导作用。处理该问题的一种方法是平滑数据,通过画估计的分布图而不是点本身(见图17-6)。我们使用称为核密度估计(krnel density estimation)的标准技术。
Lay out side-by-side plots.>par(mfrow=c(1,2)) For males and females,>dm=d[d$male,];df=d[d$female,] draw smoothed plots,>smoothScatter(df$age,df$attractive, with a color gradient,colramp=colorRampPalette(c("white","deeppink")), and aligned axes.ylim=c(0,4)) >smoothScatter(dm$age,dm$attractive, colramp=colorRampPalette(c("white","blue")),ylim=c(0,4))
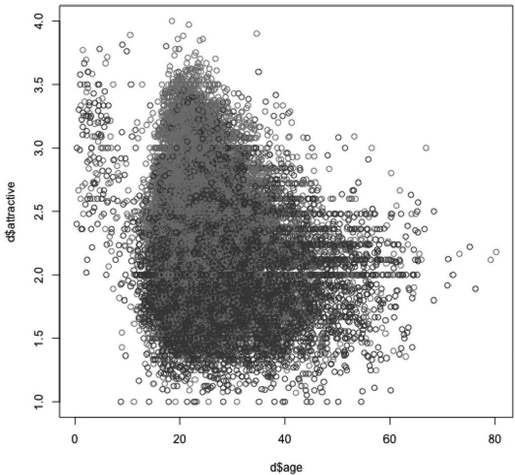
图 17-5:魅力和年龄关系的散点图,通过性别进行着色(见彩图59)
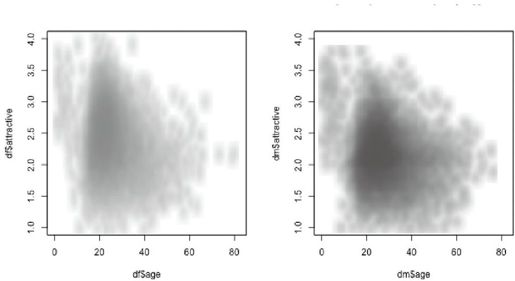
图 17-6:魅力和年龄关系的平滑散点图,每个性别一个图(见彩图60)
我们还可以试着把它们放到同一张图上(见图17-7):
>smoothScatterMult(d$age,d$attractive,d$male,blendFun=bl_burn,colramps= c(colorRampPalette(c("white","red")),colorRampPalette(c("white","blue")), colorRampPalette(c("white","green"))),pch="",nrpoints=10000)
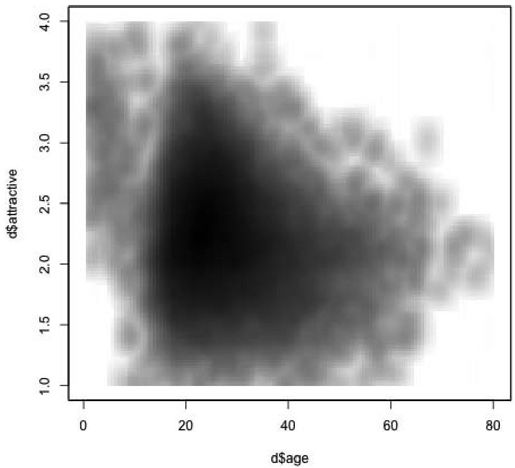
图 17-7:魅力和年龄关系的平滑散点图,通过性别着色,在一张图上交叠显示(见彩图61)
这些图形显示了数据的完全分布,但是很难看出其中的模式。举个例子,年龄如何影响魅力?通过计算总结统一和绘制它们更容易看出这一点(见图17-8a)。
For males >dm=d[which(d$male),] and females, >df=d[which(d$female),] average across faces >male_avg_by_year=by(dm$attractive, within bins cut(dm$age,breaks=0:80),mean) (oe per year) >female_avg_by_year=by(df$attractive, then cut(df$age,breaks=0:80),mean) plot them >plot(male_avg_by_year,col='blue') all together. >points(female_avg_by_year,col='deeppink')
这个图可以开始描述一个故事了,但还是有点难以理解。有些点是成千上万张脸当中的平均年龄值,而有些年龄更大的点来自少量的观察。因此,图的右侧有更多的噪音数据,因为样本更小。
我们给该图增加了两个特征(见图17-8b)。首先,我们计算了95%的置信区间,确保我们不是欺骗自己去看来自于噪音数据的模式。置信区间是通过我们有限的数据来估计可能的均值范围的一种方式。其次,我们将拟合局部加权回归(lcally weighted regression,LOESS)曲线,从而有助于对这种噪音序列数据的聚集模式进行可视化。通常,我们可能会对数据进行线性回归,但是该数据不是线性的,而且看起来不像我们所知道的任何一个函数。局部加权回归函数是拟合任意曲线到数据的一种方法。它基本上是执行代价高的移动平均值。该图还不够完美。图的两边有一些点包含一个或者两个可以计算置信区间的样本。如果你查看图17-4的年龄直方图,这些并不奇怪——看起来超过50岁的人们只占数据集的1.7%。而且,很多置信区间很大,以至于它们的数据点不是很有意义。因此,对于包含很少数据点的区域——特别年轻的和年老的——我们分别使用5年和10年这两种更大的桶。该图看起来噪音数据就少多了(见图17-8c)。
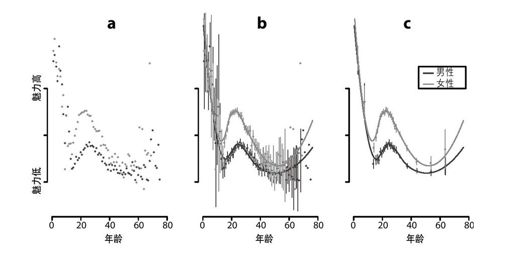
图 17-8:魅力和年龄以及性别的关系的三种迭代绘图:a)平均值在桶内区间的每个年龄;b)每个桶95%置信区间,以及局部加权回归曲线;c)更大的桶,其中数据更稀疏(见彩图62)
一般来说,在所有年龄段中,除了婴儿,女人被认为比男人更有魅力。我们发现婴儿被认为是最有吸引力(魅力)的,但是该吸引力随着年龄增长而下降,直到18岁左右(可能用户对判定青少年为“有魅力”的觉得不太自在?),然后魅力又开始上升,在27岁达到最高值。在那以后,魅力值随着年龄下降,直到50岁,在50岁年龄点,魅力值似乎又开始上升。但是很难确定,因为大于50岁的数据非常稀疏。
当然,对于20岁左右的非文本属性,存在很多关系需要探索。我们可以描绘更多类似于图17-8的图,但是我们能否马上看到所有有趣的交互?我们还是采用两两交互的方法,改变之前描绘的两两结对图。我们不是在每个面板使用散点图,而是显示单一色彩表示属性之间的全局关联。蓝色是正向关联,而红色是负向关联(见图17-9)。
First compute pairwise correlations, >cors=cor(d,use='pair') and order the attributes to try to >ord=order.hclust(cors) put similar attributes next to each other. >cors=cors[ord,ord] Plot the correlation matrix, >image(cors,col=col.corrgram(7)) with axis labels. >axis(1,at=seq(0,1,length=nrow(cors)),labels=row.names(cors))

图 17-9:Pearson关联矩阵,蓝色方块的属性对和上升的斜线是正向关联,而红色方块的属性对和下降的斜线是逆相关(见彩图63)
该绘图蕴涵了很多有趣的关联信息,这些关系值得进一步调查:
·女人被认为比男人更聪明。
·女人被认为更有可能在和狗打架中胜出。
·衣服尺寸和体重只是弱相关。
·女人更有可能被雇佣为安全巡警。
·那些看起来做过整容手术的人被雇佣为安全巡警的概率更小。
值得信任、聪明、有才华、显得年轻、富有和保守之间都两两关联。一条“责任心·轴”?
