可预料的不均衡

任何能提高我们分享、协调或行动能力的事情都会增加我们与他人一起共同追寻某些目标的自由。这么多人能如此自由地和其他人说或者做这么多的事，这在历史上是第一次。推动大规模业余化的这种自由消除了参与的技术障碍。既然现在每个人都有了各种工具可以平等地做出贡献，你可能会以为将看到平等参与的大幅增长。如果你这样想，就大错特错了。

或许你已经注意到，在本书的许多例子中参与是很不均衡的。关于沥青的维基百科文章共有129名贡献者，他们共做出了205次修改，但是其中的大多数工作是由一小部分人做的，6个人就做了将近1/4的修改量。Flickr上也出现了类似的模式：118位摄影者向Flickr提交了超过3000张美人鱼游行的照片，但其中一半来自排名前10位的提交者，其中最活跃的摄影者查琳娜，独自提交的照片达238张之多（几乎每12张中就有1张是她提交的）。这样一种形态叫做幂律分布（power law distribution），如图5—1所示。

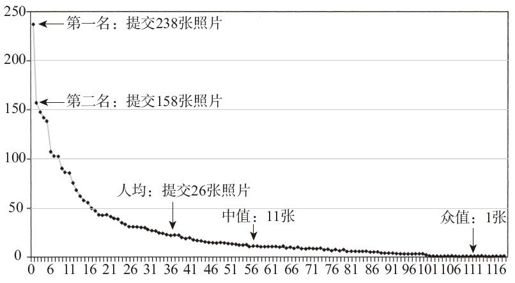
图5—1 摄影者提交2005年康尼岛美人鱼游行照片的分布情况

注：图上有五个点。最左边的两个数据点代表最活跃和次活跃的摄影者，他们都比余下的大多数摄影师活跃得多。平均提交照片的数目（总照片数除以总摄影者数）是26张，而其中值（排位在中间的摄影者所提交的数目）为11张，其众值（出现次数最多的提交数目）仅为1张。

请注意，从排名最靠前的几位提交者到大多数参与者之间照片数量的急剧下降，也请注意由于少数几位摄影者不成比例的提交量，3/4的摄影者所提交照片数量低于平均值。这个模式在社会化媒体中非常普遍：在一个有超出24个成员的邮件组里，最活跃的作者通常比排在第二位的作者活跃得多，而他比平均状态的作者则活跃得多得多。他们之间最长的交谈要比第二长的交谈长很多，而较平均长度的交谈则长得更多。博客作者、维基百科的内容提交者、摄影者、在邮件列表上交谈的人，以及其他许多大型系统里的社会参与，都呈现相似的模式特征。这里出现了两个大的意外。

第一个意外是，虽然是许多种不同类型的行为，它们这种不均衡都呈现出同一形态。Flickr网站上照片标记（或“标签”）的引用次数，与维基百科上每条目读者数及每用户提交文章数，其数据分布都具有相同的形状。将社会情境下的一组事物（可以是用户、照片、标签）按它们出现的频率排序，会呈现幂律分布的常态。你可以按一组Flickr用户提交照片的数量将他们排序，也可以对一组照片按每张的观众数排序，还可以按每个标签被应用的照片数量对它们进行排序。所有这些图形都会大致呈现幂律分布的形态。

第二个意外是，这种不均衡对大型社会系统有驱动作用而不会损害它。维基百科的用户中，提交过内容的不足总数的2％，却足以为数百万用户创造深远的价值。对于这些提交者，维基百科也从来没有用过什么办法让他们的工作更平均一些。如果考虑过减少这些不平等的话，推动维基百科发展的自发劳动分工就不可能了。相反，绝大多数大型社会实验都推动了对某种不平等现象的利用，而不是限制。尽管“生态系统”一词已经被过度使用（通常是为了让简单的情况显得更复杂），但它在这里却很适用，因为大型社会系统不应被理解为某种“平均”用户行为的简单聚合，所谓“平均”用户从来都不存在。

幂律的最显著特征就是，等级越高则越不均衡。其数学原理很简单：幂律描述的是这样一组数据，其第n个位置的秩（rank）是第1个位置的秩的1/n。对于一个纯幂律分布，第1位与第2位之间的差距要大于第2位与第3位之间的差距，以此类推。

以维基百科的文章编辑为例，你可以料到排名第2的次活跃用户的编辑量只及第1名编辑量的一半，而排名第10的只做了后者的1/10那么多。这也是所谓“80/20法则”背后的形态，按此法则，一个商店20％的存货将实现其80％的收入。

幂律进入社会科学的文献始于20世纪早期意大利经济学家维尔弗雷多·帕累托（Vilfredo Pareto）的研究，他发现在他所研究的每个国家中，财富都呈幂律分布。这个模式很普遍，他称之为“可预料的不均衡”（a predictable imbalance）。这也正是《长尾理论》（The Long Tail）一书中，克里斯·安德森（Chris Anderson）相关论述的背后形态。对于iTunes和Amazon这样的在线零售商，他们所销售的大部分商品都卖得不好，但这些商品集合起来却产生了不可小觑的收入。不过这一模式不仅适用于商品，它同样适用于社会性互动。真实世界里的各种分布形态只是这一公式的近似表现，但它所产生的不均衡在各种大型社会系统中的表现数量惊人。

不管我们怎么展示，这个形态同我们熟悉的钟形曲线分布（bell curve distribution）都很不一样。假设到你所在的社区随机选择200名男子并测量他们的身高。对像身高这样符合钟形曲线的数组，知道这些数值中任何一个，如平均值、中值或者众值，都是了解其他数值的线索。如果你知道作为中值的身高，或者这些男人中出现最多次的身高，你就可以对他们的平均身高做出有根据的推测。更关键的是，无论你知道的平均身高是多少，都可被认作对此群体最具代表性的数值。

现在，让我们假设这些身高数值不表示为钟形曲线而呈幂律分布。假设200名男子的平均身高是1.78米；最常出现的身高（或者说众值）是0.30米，这样的男子有几十个；身高的中值为0.61米（即100名男子高于0.61米，100名男子低于0.61米）。更重要的是，在这样一个分布中，5名最高男子的身高将分别为12.20米、15.24米、20.12米、30.48米和60.96米。当然人们的身高不会遵循幂律定律（如果是这样全世界的裁缝和建筑师们走运了），但是许多社会系统都遵循幂律分布。一篇维基百科文章最活跃的贡献者、Flickr上最热衷于为照片添加标签的人、一个邮件组里讲话最多的成员，他们往往都比群体里表现最平均的那个人要活跃得多。事实上，由于他们的活跃程度，对“平均”参与的任何测量失去了意义。从少数极度活跃的成员到一大群几乎不活动成员之间是陡峭的斜坡。尽管平均值很容易计算，却几乎完全不具代表性。

任何呈现幂律分布的系统，其平均值、中值和众值必然相差悬殊，这样的系统有几个奇特的结果：首先，由其定义可知，绝大多数参与者的表现都是低于平均值的。这对于许多人可能听起来很奇怪，因为我们习惯了一个平均意味着中间的世界，即平均值与中值相等。

一个经济学家的笑话可以帮你懂得“低于平均值”的现象怎样起作用：比尔·盖茨走进一个酒吧，突然里面每个人都变成了百万富翁——人均意义上的。其推论就是酒吧里其他每个人的收入都低于此平均值。

这些系统的另一个意外之处就是，当它们不断长大，其中的少数人和大多数人之间的不均衡也会变得更大，而不是更小。当我们有了更多的网络博客、更多的MySpace主页，或者更多的YouTube视频，获得最多关注的那些内容和只获得平均关注的内容之间的差距将会扩大，平均值与中值的差距也是一样。

如果你在看到某一个用户或者甚至是一小群用户时就以为他们就能代表全体，那么你是不可能了解维基百科（或者说任何大型社会系统）的。最活跃的少数用户完成了大部分的编辑工作，尽管他们只占所有贡献者里的少数并且经常是极少数。然而，即使是这一小群人也不能解释维基百科所取得的完全成功，因为许多这样的活跃用户是在纠正打字错误和做许多小的改动，而那些只编辑过一次的用户有时添加了分量重得多的相关内容。

当系统的各种成分间发生互动，而不仅是不同成分的集合，系统常呈现幂律分布。身高不是一个系统，我的身高独立于你的身高，我们两人的身高不会互相影响。可是，我使用维基百科的行为却不是独立于你的，因为你会看到我的修改，而我也会看到你的。呈幂律分布的系统令我们感到理解困难，这也是原因之一。我们已经习惯了能够从小型样本提取有用的平均值信息，再通过它们做出有关整个系统的推论。当我们遇到一个像维基百科一样、不存在典型用户的系统，源于考虑平均值的那些思维习惯不仅变得毫无用处而且是有害的。要理解像一篇维基百科文章那样的东西怎么产生，你不能去找典型贡献者，因为它不存在。相反，你必须改变自己的着眼点，集中考察集体的行为而不是个体的用户。

幂律定律也可以帮助解释，在许多小而紧密的博客朋友圈和少数那些最知名、被访问最多的网络博客之间的差别。两者所承受的不同压力表现在图5—2中，并反映了幂律分布和可被支持的交流模式两者之间的关系。

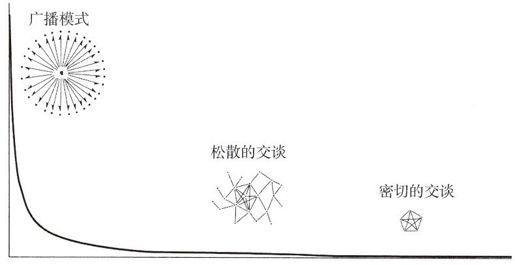
图5—2 受众规模与交谈模式之间的关系

注：曲线代表网络博客的幂律分布，按受众规模排序。图左侧的网络博客读者如此之多，作者不可能与数百万读者互动，只能限于广播模式。随读者群规模下降，受众群变小，受众可能实现松散的交谈。网络博客的长尾，即每个博客只有几位读者，能支持紧密的交谈，此时每位读者也是作者，反之亦然。

幂律分布意味着，绝大多数的作者都没有多少读者。这样的读者和作者可以给彼此大致相等的关注，形成较为紧密的谈话群。（这就是前一章所描述的小型朋友群体利用网络博客或其他社会性网络工具的模式。）当受众群体扩大到数百名，不可能再支持“每个人都和其他每个人联结”的紧密模式——交谈仍然是可能的，但社区里的联系已经松散多了。而当有数千人投以关注，有数百万人更不必说，名声就起作用了。一旦作者们开始获得比他们所能回报的更多的关注，他们就必须在深度和广度之间做出选择了。他们可以花较少的时间和每个人讲话。此时我们会说这样的互动流于表面，或者说受众被摊薄了。或者，他们选择仅限于少数几个人的深层交流。这时我们说他们搞小团体，或者说他们冷淡。极端情形下，他们可能被迫同时采用这两种策略，既限制交往广度也限制交往深度。婚礼宴会可以看做这种折中的本地版本。新娘和新郎请来一屋子都是他们可以谈很多话的人，为避免失礼却只能和绝大多数客人每人谈几分钟。