2.2　差分方程的建模方法基础

上节中，我们会发现，动态的连续模型可以采用微分方程方法建立；当时间变量离散化后，可以用差分方法建立动态离散模型．有些实际问题既可以建立连续模型，又可以建立离散模型，究竟采用哪种模型应视建模的目的而定．

下面就不同类型的差分方程进行讨论．所谓的差分方程是指：对于一个数列｛x_n ｝，把数列中的前n ＋1项x_i （i ＝0，1，2，…，n ）关联起来所得到的方程．

2.2.1　常系数线性差分方程

1．常系数线性差分方程的形式

常系数线性齐次差分方程的一般形式为：

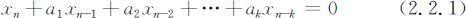
其中k 为差分方程的阶数，a_i （i ＝1，2，…，k ）为差分方程的系数，且a_k ≠0（k ⩽n ）．对应的代数方程为：

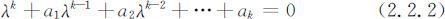
称为差分方程（2.2.1）的特征方程，其特征方程的根称为特征根．

常系数线性齐次差分方程的解主要是由相应的特征根的不同情况有不同的形式．下面分别就特征根为单根、重根和复根的情况给出差分方程解的形式．

（1）特征根为单根

设差分方程（2.2.1）有k 个单特征根λ ₁ ，λ ₂ ，…，λ_k ，则差分方程（2.2.1）的通解为：

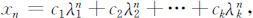
其中c ₁ ，c ₂ ，…，c_k 为任意常数，且当给定初始条件

时，可以唯一确定一个特解．

（2）特征根为重根

设差分方程（2.2.1）有l 个相异的特征根λ ₁ ，λ ₂ ，…，λ_l （1⩽l ⩽k ），重数分别为：m ₁ ，m ₂ ，…，m_l ，且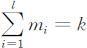 ，则差分方程（2.2.1）的通解为：

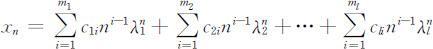
当给定初始条件（2.2.3）时，可以唯一确定一个特解．

（3）特征根为复根

设差分方程（2.2.1）的特征根为一对共轭复根λ _1，2 ＝α ±iβ 和相异的k －2个单特征根λ ₃ ，λ ₄ ，…，λ_k ，则差分方程（2.2.1）的通解为：

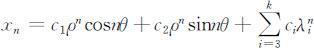
其中 ，当给定初始条件（2.2.3）时，可以唯一确定一个特解．

对于有多个共轭复根和相异实根，或共轭复根和重根的情况，都可以类似地给出差分方程解的形式．

2．常系数线性非齐次差分方程

常系数线性非齐次差分方程的一般形式为：

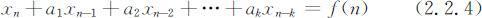
其中k 为差分方程的阶数，a_i （i ＝1，2，…，k ）为差分方程的系数，且a_k ≠0（k ⩽n ），f （n ）为已知函数．在差分方程（2.2.4）中，令f （n ）＝0，所得方程：

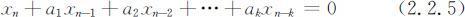
称为非齐次差分方程（2.2.4）对应的齐次差分方程，即与差分方程（2.2.1）的形式相同．

求解非齐次差分方程通解的一般方法分成两步，首先求对应的齐次差分方程（2.2.5）的通解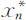 ；然后求非齐次差分方程（2.2.4）的一个特解 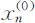．则非齐次差分方程（2.2.4）的通解为 ．

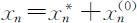关于求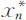 的方法同求差分方程（2.2.1）的方法相同．对于求非齐次方程（2.2.4）的特解 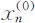的方法，可以用观察法确定，也可以根据f （n ）的特性用待定系数法确定，具体方法可参照常系数线性非齐次微分方程求特解的方法．

2.2.2　差分方程的平衡点及其稳定性

一般说来，差分方程的求解是困难的，实际中往往不需要求出差分方程的一般解，而只需要研究它的平衡点及其稳定性即可．

1．一阶线性常系数差分方程

一阶线性常系数差分方程的一般形式为：

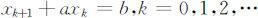
其中a，b 为常数，它的平衡点是由代数方程x ₁ ＋ax ＝b 求解得到，不妨记为x ^* ．

如果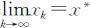 ，则称平衡点x ^* 是稳定的，否则是不稳定的．

为了便于研究平衡点x 的稳定性问题，一般将其转化为求方程x _{k ＋1} ＋ax_k ＝0的平衡点x ＝0的稳定性问题．事实上，由x _{k ＋1} ＋ax_k ＝0，容易解得：x_k ＝（－a ） ^k x ₀ ．于是x ^* ＝0是稳定的平衡点的充要条件是：|a|<1．

2．一阶线性常系数差分方程组

一阶线性常系数差分方程组的一般形式为：

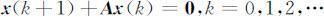
其中x （k ）为n 维向量， A 为n ×n 阶常数矩阵．

它的平衡点x ^* ＝0是稳定的充要条件是： A 的所有特征根|λ_i |<1（i ＝1，2，…，n ）．

对于一阶线性常系数非齐次差分方程组

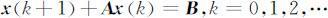
的情况同样给出．

3．二阶线性常系数差分方程

二阶线性常系数差分方程的一般形式为：

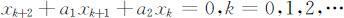
其中a ₁ ，a ₂ 为常数，它的平衡点x ^* ＝0是稳定的充要条件是：特征方程λ ² ＋a ₁ λ ＋a ₂ ＝0的根λ ₁ ，λ ₂ 满足|λ ₁ |<1，|λ ₂ |<1．

对于一般的二阶线性常系数差分方程x _{k ＋2} ＋a ₁ x _{k ＋1} ＋a ₂ x_k ＝b 的平衡点的稳定性问题同样给出．类似地，也可直接推广到n 阶线性差分方程的情况．

4．一阶非线性差分方程

一阶非线性差分方程的一般形式为：

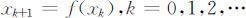
其中f 为已知函数，其平衡点定义为方程x ＝f （x ）的解x ^* ．

事实上，将f （x_k ）在x ^* 处作一阶泰勒展开有：

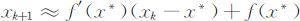
则x 也是一阶线性差分方程x _{k ＋1} ＝f ′（x ）（x_k －x ）＋f （x ）的平衡点，所以，平衡点x 稳定的充要条件是：|f ′（x ）|<1．

一般说来，要求微分方程的解析解很困难，下面介绍一些微分方程的差分方法来得到问题的数值解．

2.2.3　连续模型的差分方法

1．一阶常微分方程的差分方法

设一阶常微分方程的定解问题为：

其中f 为x，y 的已知函数，且关于y 满足利普希茨（Lipschitz）条件，y ₀ 为给定的初值．

寻求微分方程初值问题（2.2.6）在一系列离散点x ₁ <x ₂ <…<x_n <…上的近似值y ₁ ，y ₂ ，…，y_n ，…的方法即为常微分的差分方法．假设步长h＝x_n －x _{n －1} 为常数．在此，我们根据微分的差分方法，即用差商来近似代替微商，再利用“步进式”方法，可以给出求解问题（2.2.6）的差分方法．

（1）单步欧拉（Euler）公式

用差商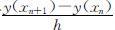 近似代替y ′（x_n ）＝f （x_n ，y （x_n ））中的导数，即可得差分公式：

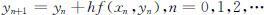
其精度为o （h ² ）阶的．

（2）两步欧拉公式

用差商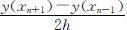 近似代替y ′（x_n ）＝f （x_n ，y （x_n ））中的导数，即可得差分公式：

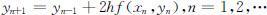
两步法需要用到前两步的信息，一般不能自行起步，需先用单步法求出y ₁ ，其精度为o （h ³ ）阶的．

（3）梯形公式

首先对方程y ′＝f （x，y ）的两边在［x_n ，x _{n ＋1} ］上求积分，得：

然后，利用积分的梯形公式求解积分：

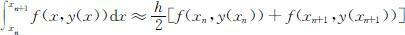
则有： ，离散化后，可得微分方程的梯形差分公式：

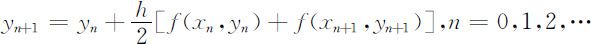
这是一个隐式格式，计算量较大，一般不单独使用．其精度为o （h ³ ）阶的．

（4）改进欧拉公式

由于单步欧拉公式精度低，但计算量小；矩形公式精度高，但计算量大，为此，将两者综合起来，得到改进的欧拉公式，其精度为o （h ³ ）阶的．

预测：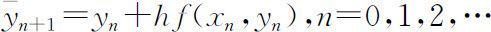

校正：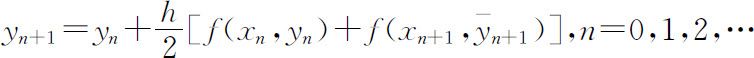

或写成平均化形式：

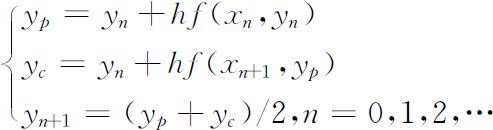
这种公式更适合于计算机编程．

（5）龙格—库塔（Runge—Kutta）方法

设y （x ）为初值问题（2.2.6）的准确解，根据微分中值定理有：

存在η_n ∈（x_n ，x _{n ＋1} ），使

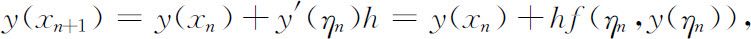
其中f （η_n ，y （η_n ））为解曲线y （x ）在区间［x_n ，x _{n ＋1} ］上的平均斜率．可见，只要能对平均斜率提供一种近似计算方法，就能得到一种对应的差分格式．由此，如果在区间［x_n ，x _{n ＋1} ］内多预测几个点的斜率，用它们的加权平均代替平均斜率，则有可能构造精度更高的公式．

讨论有m 个点的情形．设m 个点的横坐标为：x_n ，x_n ＋a ₂ h，x_n ＋a ₃ h ，…，x_n ＋a_m h ．令：

其中a_i ，b_ij ，c_i 都是与f，n 无关的常数，其值应使上述公式（2.2.7）的精度达到尽可能高，该公式称为m 级Runge—Kutta公式，简称为R—K公式．

当m ＝2时，令a ₂ ＝b ₂₁ ＝a ，有如下的二级R—K公式：

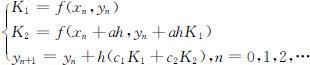
其中a，c ₁ ，c ₂ 为待定的参数．特别的取 ，即为改进的欧拉公式；或者取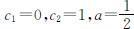 ，称为变形的欧拉公式．

当m ＝4时，同样可以得到一个四阶Runge—Kutta公式．最常用的四阶标准R—K公式为：

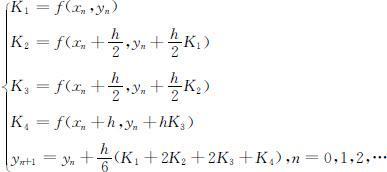
2．一阶常微分方程组的差分方法

将前面的单个方程中的变量和函数视为向量，相应的差分方法即可用于由多个方程组成的一阶方程组的情形．

对于2个方程的方程组：

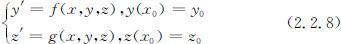
设以y_n ，z_n 表示函数在结点x_n ＝x ₀ ＋nh （n ＝1，2，…）上的近似值，则有改进的欧拉公式：

四阶龙格—库塔公式：

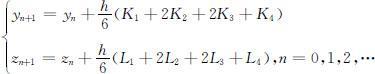
其中：

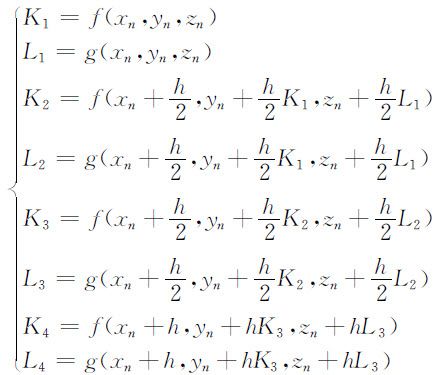
其他的公式也都可以类似得到，即相当于同时求解多个一阶方程，从方法上没有本质的区别．

3．高阶常微分方程的差分方法

对于某些高阶方程的定解问题，原则上可以转化为一阶方程组来求解见如下的二阶微分方程的定解问题：

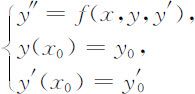
若令z ＝y ′，则可化为一阶方程组的定解问题：

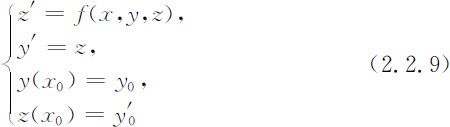
实际上，（2.2.9）式可看成是（2.2.8）式的特例，类似的可以得到相应的求解差分公式．