6.3　层次分析法建模案例

例 　公务员招聘问题^［18］

6.3.1　问题提出

公务员招聘要求对应聘人员的面试成绩和面试专家组意见综合衡量后，确定应聘人员的录用与否，合理量化评价应聘人员是保证公务员招聘公平公正的基础．

6.3.2　模型的建立

对于N 个应聘人员，M 个用人单位，录用K 个人员的公务员招聘情况进行讨论．首先对于应聘人员的笔试成绩和面试的专家组意见化为对于工作的权重，然后利用权重建立公务员招聘方案的模型．

6.3.2.1　应聘人员对各部门权重的评定

1．对于面试成绩的权重评定

通过每个人的能力等级与各个工作要求进行比较，我们发现只有1、2、4三个人满足第二项工作类别要求，其余均不能达到各工作类别的要求，为选拔人才，我们认为工作单位应当适当降低要求，在这里我们引入权重的概念来标识各个应聘者对工作的适合程度．我们认定应聘者能力满足工作期望要求时，权重设定为1，能力与期望水平稍差时，权重设定为1/2；能力与期望水平明显相差很多时，权重设定为1/4；能力与期望水平相差特别大时，权重设定为1/8．

（1）求各种能力对不同工作的权重

我们可以从单一工作类别出发来求解各个权重，这样可以使复杂的问题简化．求各种能力对不同工作的权重时，我们采用了层次分析法的思想．在这种方法中，需要先建立成对比较矩阵．如对工作类别①，要求应聘人员的理解能力和表达能力最高（A ），其次为知识面（B ），最后为应变能力（C ），故得成对比较矩阵如下：

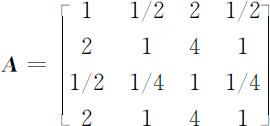
其中a ₁₂ ＝1/2即表示知识面和理解能力对工作类别①的重要性之比为1∶2，a ₂₃ ＝4即表示知识面和理解能力对工作的重要性之比为4∶1．求出对比矩阵 A 的最大特征根为λ ＝4.0000，对应的特征向量归一化后为

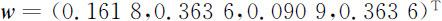
即为四种能力对于工作类别①的权重．由此可知理解能力和表达能力对工作类别①的权重最大，其次为知识面，最后是应变能力．同理可求得四种能力对于其他三个工作类别的权重，从而得四种能力分别对于四种工作类别的权重矩阵

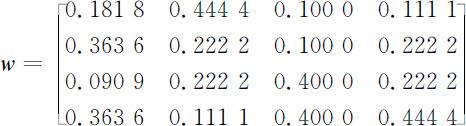
（2）确定在同一工作类别下应聘人员对四种能力的权重

先确定比较标准：我们认定应聘者能力满足工作希望要求，设定为1；能力与希望水平稍差，设定为1/2；能力与希望水平明显相差，设定为1/4；能力与希望水平相差特别大，设定为1/8．

应聘者的四项能力评定结果与该工作类别下对四种能力的要求按上面的标准进行比较，得该应聘者在这一工作类别下对四种能力的权重．

在以上比较标准下，四种能力的成对比较矩阵是一致阵．将N 个应聘者的权重组合构成权重矩阵 B _{N ×4} ．

（3）确定应聘人员面试成绩在工作类别①的最终权重

令 C _{N 1} 为各应聘者对于工作类别①的权重向量，则 C _{N 1} ＝B _{N 1} ×w ₁ ，其中w ₁ 表示矩阵w 的第一列向量．

（4）重复（2），（3）两步，按步骤（3）中的方法分别求各应聘者对于工作类别②，③，④的权重向量： D _{N 1} ， E _{N 1} ， F _{N 1} ．将求得的权重向量 C _{N 1} ， D _{N 1} ， E _{N 1} ， F _{N 1} 组合在一起得矩阵 B _{N ×4} ．

2．笔试成绩的权重评定

我们取笔试成绩中最高得分的权重为1，其他笔试成绩与之相比的比值作为该人员笔试成绩的权重．

3．综合权重设定

设r 为笔试权重与面试权重的比例系数，当r ＝1时，标志笔试与面试同等重要．r 具体取值由主管部门对笔试成绩的认可程度决定．

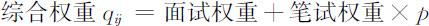
即算出各个应聘人员对各个工作类别的综合权重矩阵 Q ．

6.3.2.2　人员录用分配模型

设人员录用情况0-1矩阵为 X ，x_ij 是其中元素

（1）不考虑应聘人员的意愿，按照部门需要择优录取

若使分配合理，有利于发挥个人特长和能力，则应使总的权重最大．每个单位至少分配一个人，每个人只能分配到一个单位工作，设工作类别①包括M ₁ 个用人单位，工作类别②包括M ₂ 个用人单位，工作类别③包括M ₃ 个用人单位，工作类别④包括M ₄ 个用人单位，M ₁ ＋M ₂ ＋M ₃ ＋M ₄ ＝M ，列出整数规划模型：

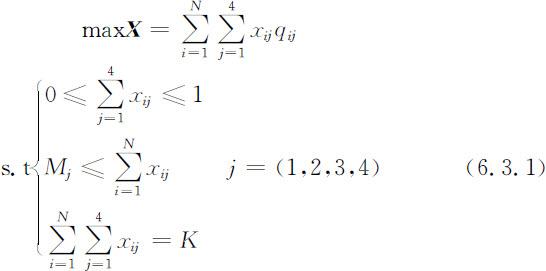
算出x_ij 的值，确定矩阵 X 即为所求得的最优分配方案．

（2）考虑应聘人员的意愿和部门需要时的录取方案

按照每个应聘人员报两个志愿建立矩阵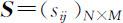

将矩阵 S 与权重矩阵 Q 的对应元素分别相乘，得到矩阵 P ，即考虑应聘人员志愿后应聘人员对各个工作的最终权重矩阵，再用p_ij 替换（6.3.1）中的q_ij ，其余步骤和上一步相同，计算出X_ij 的值，确定矩阵 X ₂ ，即可求出考虑应聘人员的意愿和用人部门的希望时的最优分配方案．