5.2 主成分分析
在实际问题中,为了尽可能完整地获取有关的信息,往往需要考虑众多的变量,这虽然可以避免重要信息的遗漏,但增加了分析的复杂性.一般说来,同一问题所涉及的众多变量之间会存在一定的相关性,这种相关性会使各变量的信息有所“重叠”.因此自然想到,能否从这多个变量中构造出很少几个综合指标,而这较少的综合指标就能综合反映原来较多指标的信息,相互之间又尽可能不重复信息?这就是主成分分析的内容.主成分分析便是在这种降维的思想下产生的处理高维数据的统计方法.
5.2.1 总体主成分
(1)总体主成分的定义
设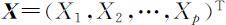 为p 维随机变量,其协方差矩阵(记为Cov( X ))为
为p 维随机变量,其协方差矩阵(记为Cov( X ))为
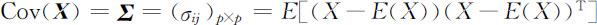
它是一个p 阶非负定方阵.
按照主成分分析的思想,我们首先构造X 1 ,X 2 ,…,Xp 的线性组合
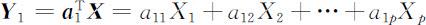
确定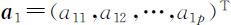 ,使得
,使得
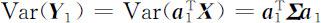
达到最大.但必须对 a 1 加以限制,否则Var( Y 1 )无界.根据在坐标旋转之下相应的组合系数向量具有单位长度这一性质,因此一个自然的约束条件是要求 a 1 的长度为1,即在约束条件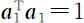 之下,求 a 1 使得
之下,求 a 1 使得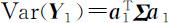 达到最大.由此 a 1 所确定的随机变量
达到最大.由此 a 1 所确定的随机变量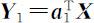 称为 X 的第一主成分.
称为 X 的第一主成分.
如果第一主成分 Y 1 在 a 1 方向上的分散性还不足以反映原变量的分散性(或称为信息),则再构造X 1 ,X 2 ,…,Xp 的线性组合
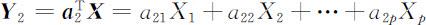
为使 Y 1 和 Y 2 所反映的原变量的信息不相重叠,要求 Y 1 与 Y 2 不相关,即
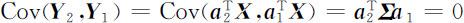
按主成分分析思想,问题转化为在约束条件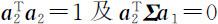 之下,求 a 2 使得
之下,求 a 2 使得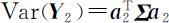 达到最大.由此 a 2 所确定的随机变量
达到最大.由此 a 2 所确定的随机变量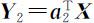 称为 X 的第二主成分.
称为 X 的第二主成分.
一般地,若 Y 1 , Y 2 ,…, Y k -1 还不足以反映原变量的信息,则进一步构造X 1 ,X 2 ,…,Xp 的线性组合
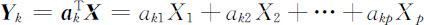
在约束条件 之下,求 a k 使
之下,求 a k 使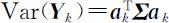 达到最大.由此 a k 所确定的随机变量
达到最大.由此 a k 所确定的随机变量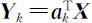 称为 X 的第k 个主成分.
称为 X 的第k 个主成分.
按上述方法,我们最多可以构造出p 个方差大于零的主成分.事实上,若有p +1个主成分 Y 1 ,Y 2 ,…, Y p +1 ,其方差均大于零,则由于 a 1 , a 2 ,…, a p +1 这p +1个p 维单位向量必线性相关,从而不妨设 a p +1 =l 1 a 1 +l 2 a 2 +…+lp a p 且l 1 ≠0,则有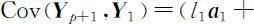
 ,这与主成分的要求相矛盾.
,这与主成分的要求相矛盾.
(2)总体主成分的求法
求总体主成分归结为求 X 的协方差矩阵 Σ 的特征值和特征向量问题,具体有如下结论:
设 Σ 是 X =(X 1 ,X 2 ,…,XP )T 的协方差矩阵,其特征值按大小顺序排列为λ 1 ⩾λ 2 ⩾…⩾λp ⩾0,相应的正交单位化特征向量为 e 1 , e 2 ,…, e p ,则 X 的第k 个主成分可表示为
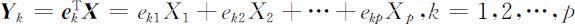
其中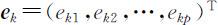 ,这时有
,这时有
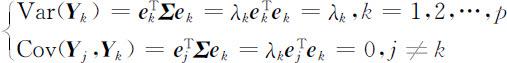
事实上,令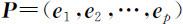 ,则 P 为正交矩阵,且
,则 P 为正交矩阵,且
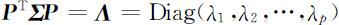
其中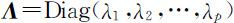 表示对角矩阵.
表示对角矩阵.
若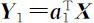 为 X 的第一主成分,其中
为 X 的第一主成分,其中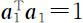 ,令
,令

则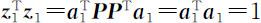 ,且
,且
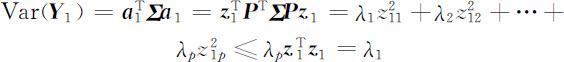
并且当 z 1 =(1,0,…,0)T 时,等号成立,这时
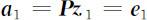
由此可知,在约束条件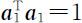 之下,当 a 1 = e 1 时,Var( Y 1 )达到最大,且
之下,当 a 1 = e 1 时,Var( Y 1 )达到最大,且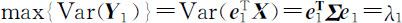 .
.
设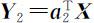 为 X 的第二主成分,则应有
为 X 的第二主成分,则应有
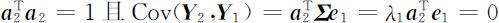
首先我们选择 a 2 与 e 1 正交(即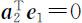 ),令
),令

则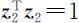 ,而由
,而由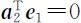 即有
即有
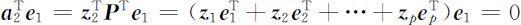
故
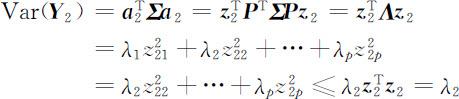
当 z 2 =(1,0,…,0)T 时,即 a 2 = Pz 2 = e 2 时,满足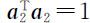 ,且
,且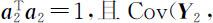
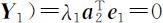 ,并且使Var( Y 2 )=λ 2 达到最大.
,并且使Var( Y 2 )=λ 2 达到最大.
上述结果表明,求 X 的主成分等价于求它的协方差矩阵 Σ 的所有特征值及相应的正交单位化特征向量.按特征值由大到小所对应的正交单位化特征向量为组合系数的X 1 ,X 2 ,…,Xp 的线性组合分别为 X 的第一、第二、直至第p 个主成分,而各主成分的方差等于相应的特征值.
(3)总体主成分的性质
①主成分的协方差矩阵及总方差
记 Y =(Y1 ,Y2 ,…,Yp )T 为p 个主成分构成的随机向量,则 Y = P T X ,其中 P =( e 1 , e 2 ,…, e p )为 Σ 的p 个正交单位化特征向量构成的正交矩阵. Y 的协方差矩阵为
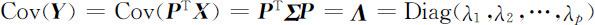
各主成分的总方差为
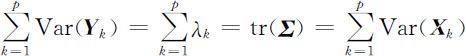
即主成分分析把p 个原始变量X 1 ,X 2 ,…,Xp 的总方差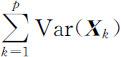 分解成p 个不相关变量Y 1 ,Y 2 ,…,Yp 的方差和,且使得Var( Y k )=λk (k =1,2,…,p ).
分解成p 个不相关变量Y 1 ,Y 2 ,…,Yp 的方差和,且使得Var( Y k )=λk (k =1,2,…,p ).
②主成分的贡献率与累计贡献率
由上式可知,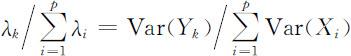 描述了第k 个主成分提取的X 1 ,X 2 ,…,Xp 的总(分散性)信息的份额,我们称此为第k 个主成分Yk 的贡献率.第一主成分的贡献率最大,表明Y1 综合原始变量信息的能力最强,其他主成分综合原始变量信息的能力依次减弱.
描述了第k 个主成分提取的X 1 ,X 2 ,…,Xp 的总(分散性)信息的份额,我们称此为第k 个主成分Yk 的贡献率.第一主成分的贡献率最大,表明Y1 综合原始变量信息的能力最强,其他主成分综合原始变量信息的能力依次减弱.
前m 个主成分的贡献率之和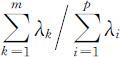 称为Y 1 ,Y2 ,…,Ym 的累计贡献率,它表明前m 个主成分综合X 1 ,X 2 ,…,Xp 的信息的能力,实际应用中,通常选取m <p ,使前m 个主成分的累计贡献率达到一定的比例(如80%~90%),这样用前m 个主成分Y1 ,Y2 ,…,Ym 代替原始变量X 1 ,X 2 ,…,Xp ,不但可使原始变量的维数降低,而且也不至于损失原始变量中的太多信息.
称为Y 1 ,Y2 ,…,Ym 的累计贡献率,它表明前m 个主成分综合X 1 ,X 2 ,…,Xp 的信息的能力,实际应用中,通常选取m <p ,使前m 个主成分的累计贡献率达到一定的比例(如80%~90%),这样用前m 个主成分Y1 ,Y2 ,…,Ym 代替原始变量X 1 ,X 2 ,…,Xp ,不但可使原始变量的维数降低,而且也不至于损失原始变量中的太多信息.
(4)标准化变量的主成分
在实际问题中,不同的变量往往有不同的量纲,由于不同的量纲会引起各变量取值的分散程度差异较大,这时变量的总方差则主要受方差较大的变量控制,若由原变量的协方差矩阵出发进行主成分分析,则优先照顾了方差较大的变量,这不但会给主成分变量的解释带来困难,有时还会造成不合理的结果.为了清除原变量彼此方差差异过大的影响,通常将原变量进行标准化再作主成分分析.
对于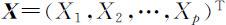 ,设
,设
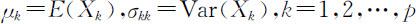 ,则其标准化变量为
,则其标准化变量为
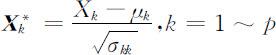
这时,对于一切1⩽k ⩽p ,均有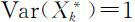 令
令
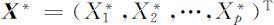
则其协方差矩阵
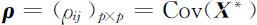
便是 X 的相关系数矩阵,其中
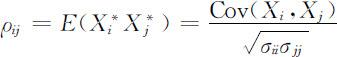
对标准化向量 X * 作主成分分析,即求 X 的相关系数矩阵 ρ 的特征值及相应的正交单位化特征向量,从而有如下结论:
标准化随机向量 的第k 个主成分可表示为
的第k 个主成分可表示为
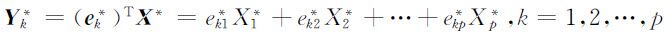
并且有
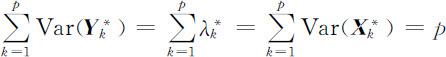
其中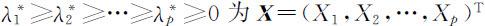 的相关系数矩阵 ρ 的特征值,
的相关系数矩阵 ρ 的特征值,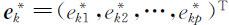 为相应于
为相应于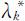 的正交单位化特征向量(k =1,2,…,p ).这时,第k 个主成分
的正交单位化特征向量(k =1,2,…,p ).这时,第k 个主成分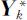 的贡献率为
的贡献率为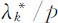 ,前m 个主成分
,前m 个主成分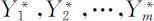 的累计贡献率为
的累计贡献率为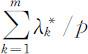 .
.
5.2.2 样本主成分
在实际问题中,总体 X =(X 1 ,X 2 ,…,Xp )T 的协方差矩阵 Σ (或相关系数矩阵 ρ )一般是未知的,具有的资料只是来自于 X 的一个容量为n 的样本观测数据

这时,我们便可用其样本协方差矩阵 S 或样本相关系数矩阵 R 分别作为 Σ 或 ρ 的估计进行主成分分析,而由 S 或 R 求得的主成分称为样本主成分.由第4章知
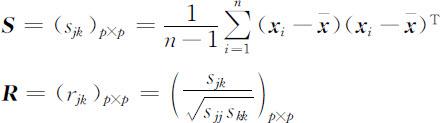
其中
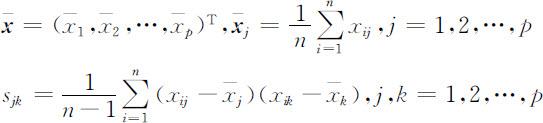
关于 S 的样本主成分,我们有如下讨论:
设 S =(sij )p×p 为样本协方差矩阵,其特征值为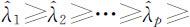 0,相应的正交单位化特征向量为
0,相应的正交单位化特征向量为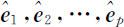 ,这里
,这里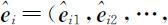
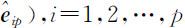 .则第k 个样本主成分可表示为
.则第k 个样本主成分可表示为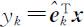 ,其中 x =(x 1 ,x 2 ,…,Xp )T 表示
,其中 x =(x 1 ,x 2 ,…,Xp )T 表示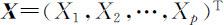 的观测值.当依次代入观测值
的观测值.当依次代入观测值 时,便得到第k 个样本主成分yk 的n 个观测值yik (i =1,2,…,n ),我们称之为第k 个样本主成分的得分.这时容易证明
时,便得到第k 个样本主成分yk 的n 个观测值yik (i =1,2,…,n ),我们称之为第k 个样本主成分的得分.这时容易证明
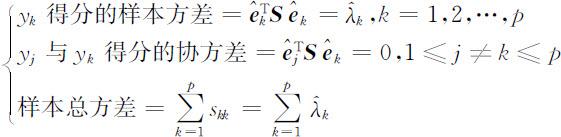
第k 个样本主成分的贡献率为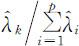 ,
,
前m 个样本主成分的累计贡献率为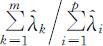 .
.
从样本相关系数矩阵 R 出发进行主成分分析,即相当于从标准化样本
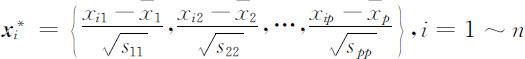
的样本协方差矩阵出发进行主成分分析,只要求出 R 的特征值及相应的正交单位化特征向量,则类似于上述的结果均成立,这时标准化样本的样本总方差为p .
需要指出的是,关于主成分的实际意义,要结合具体问题和有关的专业知识才能给出合理的解释.虽然利用主成分本身可对所研究的问题在一定程度上做分析,但主成分分析往往并不是最终目的,进而利用少数几个主成分的得分为新数据,对其再做进一步分析,如基于主成分的回归分析,聚类分析等.
5.2.3 主成分分析案例
(1)问题的提出[16]
现代物流被喻为经济发展的加速器,是推动21世纪经济发展的重要支柱产业和新的利润源.物流的发展在一定程度上推动了区域经济的发展,而区域经济的发展又会促进区域物流的集约性、规模性,二者相互促进发展.目前,我国一些地区的物流发展水平在一定程度上制约了区域经济的发展,对此在分析区域物流定位影响因素的基础上,提出主成分分析方法的区域物流定位数学模型,使城市物流的发展在区域物流规划定位中更加科学与客观.
(2)主成分分析方法模型的建立
确定城市物流在区域物流中的定位时,根据主要影响因素(指标)对周边区域及周边城市进行比较分析,确定该城市物流在区域物流网络中定位的相对重要性.目前,从强调物流规划要与区域经济、产业带发展、运输量、贸易量相结合的角度,大多采用定性的方法进行区域物流的定位分析,较少采用定量的方法进行定位分析.由于影响区域物流的因素较多,经过仔细筛选后,彼此间仍难免存在一定的相关性,因而反映的信息在一定程度上有所重叠.主成分分析法利用降维的思想,把原来较多的评价指标用较少的综合主成分指标来代替,保留原变量的绝大多数信息,且彼此间互不相关,能够使复杂问题简单化.
①对m 个样本的n 个指标进行标准化处理.标准化处理的计算公式为:
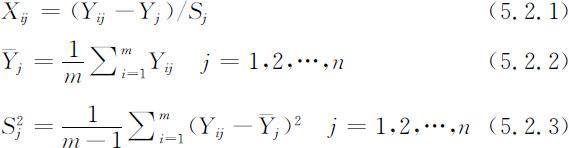
经标准化处理后可得到标准化矩阵 X .
②计算相关系数,得到相关矩阵.计算标准化后的每两个指标间的相关系数,得到相关系数矩阵 R ,即n 个指标的协方差矩阵. R 矩阵的元素与样本的方差和协方差有关.相关系数的计算公式为:
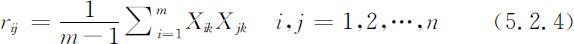
R 矩阵是一个实对称的矩阵,其主对角线上元素rij 均为1.
③计算矩阵 R 的特征根及相应的特征向量.根据得到的相关矩阵 R ,可求出 R 的特征值:

得到n 个非负特征根λ 1 ⩾λ 2 ⩾…⩾λn ⩾0,从而得到对应于特征根的n 个单位化特征向量,构成一个正交矩阵,记为 a .
④计算主成分.对于全部m 个样本,则有:

式中: Z 0 为样本主成分; X 0 为标准化样本.
⑤主成分选择.为了合理选择少数几个主成分来有效描述原来n 个指标所构成的一组样本,引入主成分贡献率及其计算方法.若λi 为相关矩阵 R 的第i 个特征根,则第k 个主成分的方差贡献率为:

前r 个主成分的累计方差贡献率为:
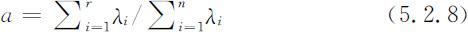
累计方差贡献率达到一定数值时,取前r 个主成分,即认为这r 个主成分就以较少的指标综合体现了原来n 个评价指标的信息.
⑥用各主成分的方差贡献率作为权重,线性加权求和得到主成分表达式:
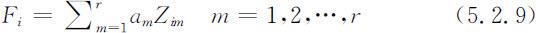
Fi 反映了第i 个地区r 个主成分的贡献率,Fi 值越高,说明该地区r 个主成分的重要性越高;反之,重要性越弱.以每个主成分对应的特征值占所提取主成分总的特征值之和p 的比例作为权重计算综合主成分评价模型:
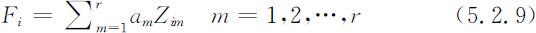
式中:F 为m 个样本的综合函数得分,以该得分来进行排序和评价.
(3)实例验证
区域的中心城市对区域物流的形成和发展具有重要影响,区域物流的发展基本上是以中心城市为核心向区域内的周边地区进行辐射和蔓延.为制定某地区的物流规划,选取其中4个主要城市A、B、C、D作为重要考虑范畴.根据国内外的统计方法,物流业的产值都是按交通运输、仓储、邮电通信业、批发和零售等行业的最大口径来进行统计的,故对4个城市的经济状况主要选取9个指标:x 1 为生产总值(亿元);x 2 为人口数(万人);x 3 为全社会固定资产投资(亿元);x 4 为货运量(万吨);x 5 为货物周转量(亿吨·千米);x 6 为货物进出口总额(万美元);x 7 为社会消费品总额(亿元);x 8 为交通运输、邮电通信业职工人数(人);x 9 为居民消费水平.4个城市的相关指标如表5.3所示.
