7.3　最短路径算法

最短路径算法在数学建模中的应用相当广泛，数学建模竞赛中的赛题中也经常出现，如2007年的“乘公交，看奥运”、2011年的“交巡警服务平台的设置与调度”等．

在一个网络中，如果两个结点之间有直接的因果关系，则这两个结点直接连通，在连接两个结点的弧上标上它的代价或权，值得注意的是这样的代价不一定是对称的，即A 到B 的代价不一定等于B 到A 的代价，实际问题中以行船为例，有顺水和逆水的区别．在图G 中，给出两个结点求这样一条最短的路径，使经过这条路径上的代价之和最小，这就是最短路径问题．

7.3.1　Dijkstra算法

A　基本概念

在无向图G ＝（V，E ）中，假设每条边E ［i ］的长度为w ［i ］，找到由顶点u ₀ 到其余各点的最短路径．迪克斯特拉算法用来解决从顶点u ₀ 出发到其余顶点的最短路径，该算法按照最短路径长度递增的顺序产生最短路径．

B　算法描述

迪克斯特拉（Dijkstra）算法的基本思想是按距u ₀ 从近到远为顺序，依次求得u ₀ 到G 的各顶点的最短路径和距离，直至v ₀ （或直至G 的所有顶点），算法结束．为避免重复并保留每一步的计算信息，采用了标号算法．下面是该算法．

（i）令l （u ₀ ）＝0，对v ≠u ₀ ，令l （v ）＝∞，S ₀ ＝｛u ₀ ｝，i ＝0．

（ii）对每个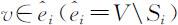 ，用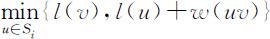 代替l （v ）．计算 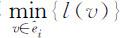，把达到这个最小值的一个顶点记为u _{i ＋1} ，令 ．

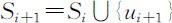（iii）若i ＝|V|-1，停止；若i<|V|-1，用i ＋1代替i ，转（ii）．

算法结束时，从u ₀ 到各顶点v 的距离由v 的最后一次的标号l （v ）给出．在v 进入S_i 之前的标号l （v ）叫T 标号，v 进入S_i 时的标号l （v ）叫P 标号．算法就是不断修改各顶点的T 标号，直至获得P 标号．若在算法运行过程中，将每一顶点获得P 标号所由来的边在图上标明，则算法结束时，u ₀ 至各顶点的最短路径也在图上标示出来了．

C　Matlab程序

function［weight，path］＝dijkstar（a）

pb（1∶length（a））＝0；％pb记录是否标号

pb（1）＝1；

index1＝1；％index1记录标号顺序

index2＝ones（1，length（a））；％index2记录标号的前一结点号，便于最后寻找路径

d（1∶length（a））＝inf；％d中初始为inf，后面再修改．

d（1）＝0；％第一个顶点到自身的距离自然是0

temp＝1；％初始由第一点开始寻找

while sum（pb）<size（a，2）％终止条件为pb中的点全部标号（用1表示已标号，0表示未标号）

tb＝find（pb＝＝0）；％找出未标号的点向量

d（tb）＝min（d（tb），d（temp）＋a（temp，tb））；％替换过程默认1号点为始发点

tmpb＝find（d（tb）＝＝min（d（tb）））；％找出最小的距离进行标号

temp＝tb（tmpb（1））；％同上可能有多个点的权值达到最小，故取1号点对应的点号

pb（temp）＝1；％正式标号

index1＝［index1，temp］；％将标号的点归入index1中，在下次搜索中失去候选资格

index＝index1（find（d（index1）＝＝d（temp）-a（temp，index1）））；

％以下程序全为找到路径的向量

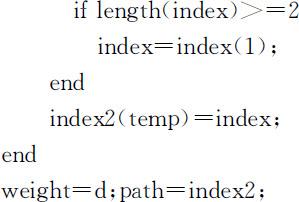
D　实例

例：对下列带权无向图，利用上述函数进行计算1点到其他各点的距离和路径．

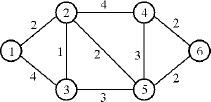
e给出了从1点到其他点的最短距离，t给出了从1点到其他点的路线，t的第6个元素是5，第5个元素是2，第2个元素是1，故1→6的路径为1→2→5→6．

7.3.2　Floyd算法

A　基本概念

Floyd算法是求任意两结点间的最短路径．显然，Floyd算法可以使用dijkstra算法n 次完成，时间复杂度是O （n ^3）．

Floyd还提出过另一个算法，同样是O （n ^3）的复杂度，但形式上更简单些．

要求的解是一个矩阵S ［N ×N ］，其中S ［i ］［j ］表示结点i 到j的最短路径，算法很像动态规划算法，甚至更简单些，不同的是这里规划的是一个矩阵，而不是简单的数组．

B　Floyd算法过程

Floyd算法过程描述如下：

Step1：首先S 以边集M 初始化，得到所有的直接连通代价；

Step2：依次考虑第k 个结点，对于S 中的每一个S ［i ］［j ］，判断是否满足：

S ［i ］［j ］>S ［i ］［k ］＋S ［k ］［j ］，如果满足则用S ［i ］［k ］＋S ［k ］［j ］代替S ［i ］［j ］，此为第k 步；

Step3：k 循环取遍所有结点，算法结束时，S 为最终解．

C　Floyd算法的Matlab程序

function［shortpath，nextnode］＝floyd（vex，k）

％vex是邻接矩阵，shortpath返回最短路径矩阵，nextnode返回路线经过的结点构成的矩阵

D　实例

对于上述例子，用floyd算法计算任意两点的最短路径和路线．

M＝inf；

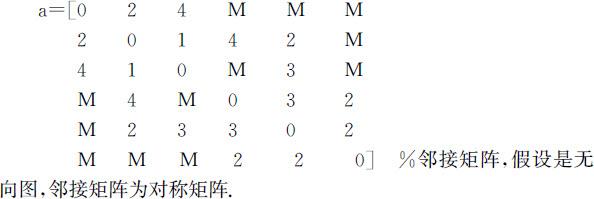
［S，R］＝floyd（a，6）；

通过上程序计算得：

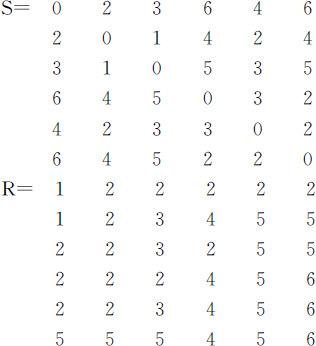
结果说明：

S 矩阵第1行，第6列的值为6，表示从第1点到第6点的最短路径为6． R 矩阵第1行第6列的值为2，第2行第6列的值为5，而第5行第6列的值为6，因此，1—6的最短路线为：1—2—5—6．

S 矩阵第3行，第4列的值为5，表示从第3点到第4点的最短路径为5． R 矩阵第3行第4列的值为2，第2行第4列的值为4，因此，3—4的最短路线为：3—2—4．