图6.4　层次结构模型

（2）构造成对比较矩阵

（S1）构建目标层A对准则层B ₁ ，B ₂ ，B ₃ ，B ₄ ，B ₅ 的成对比较矩阵为：

（S2）构建准则B ₁ ，B ₂ ，B ₃ ，B ₄ ，B ₅ 相对于P ₁ ，P ₂ ，P ₃ 的成对比较矩阵

①B ₁ 对P ₁ ，P ₂ ，P ₃ 作用的成对比较矩阵：

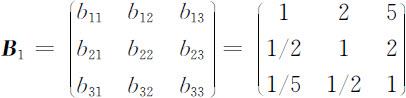
②同样B ₂ 、B ₃ 、B ₄ 、B ₅ 对P ₁ ，P ₂ ，P ₃ 作用的成对比较矩阵为：

（3）计算特征值和特征向量

下面，利用“和法”求A 的特征向量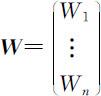 和特征根λ _max

（S1）将 A ＝（W_ij ） _{n ×n} 的元素按列归一化得：

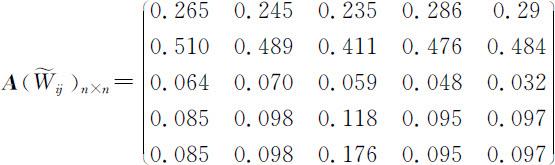
（S2）将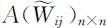 中元素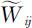 按行求和得各行元素之和：

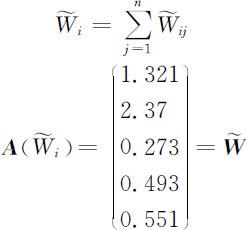
（S3）再将上述矩阵向量归一化得到特征向量近似值

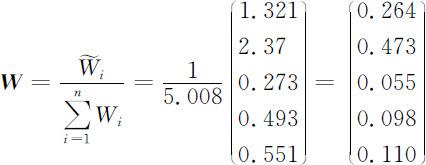
其中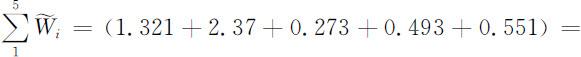

（S4）计算与特征向量相对应最大特征根（近似值）

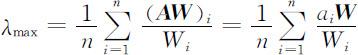
故有最大特征根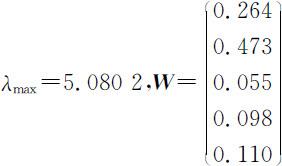

同理，可计算得出成对比较矩阵 B ₁ ， B ₂ ， B ₃ ， B ₄ ， B ₅ 的最大特征根及权向量（如表6.5）．