4.3　数值微积分

在工程实践与科学应用中，经常要计算函数的积分与微分．当已知函数形式求函数的积分时，理论上可以利用牛顿—莱布尼茨公式来计算．但在实际应用中，经常接触到的许多函数都找不到其积分函数，或者函数难以用公式表示（如只能用图形或表格给出），或者有些函数在用牛顿—莱布尼兹公式求解时非常复杂，有时甚至计算不出来．微分也存在相似的情况，此时，需考虑这些函数的积分和微分的近似计算．

4.3.1　差分与数值微分

一般情况下，我们在实际中所获取的数据都是离散型的，对已知离散点对（x_i ，y_i ）i ＝0，1，…，n ，如何估计系统在结点处的变化率——在结点处的导数值？一般用邻近弦的斜率近似代替该点切线的斜率（结点处导数值），即：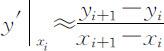

称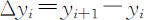 为y 在i 处的差分，因此有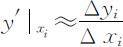： ，当两结点很近（Δx_i 很小）时，计算的误差是可以接受的，或可以控制的．因此对离散点或已知复杂函数在结点处的导数值可以通过差分之比（称为差商）来近似获得．

在MATLAB中提供了函数diff，可以计算离散点列的差分序列，因此通过diff函数可以近似计算已知点对在结点处的导数值，（diff函数还可以计算已知函数的导数的解析式，见下节符号运算）．

格式1：diff（x）　返回x对预设独立变量的一次差分；

格式2：diff（x，n）　返回x对预设独立变量的n次差分（二次差分是差分的差分，依此类推）；

注1：（x_i ，y_i ）i ＝0，1，…，n 在结点的一阶导数可近似表成：diff（y）./diff（x）；

注2：diff（y）./diff（x）表达的导数是从第2点开始的；

注3：一般结点x 取等距结点；

注4：一阶导数可近似表成：diff（y）./diff（x），但n 阶导数不能表成diff（y，n）./diff（x，n）．

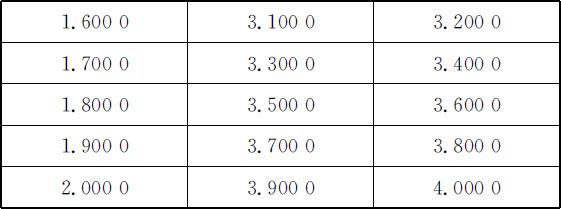
【例】　计算y ＝x ² ＋1在［1，4］的某些点数值微分，并与其真实值进行比较．

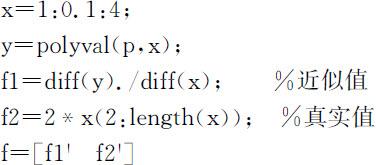
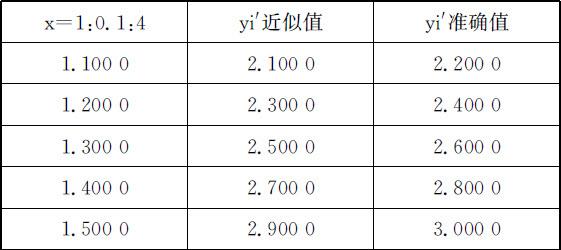
续表

4.3.2　Newton-cotes数值积分

计算积分有牛顿—莱布尼茨公式（求精确解）和数值积分（求近似解）两种方法，Matlab提供了int（）函数求出原函数，再用牛顿—莱布尼茨公式计算定积分．这种方法在符号计算里再行介绍．

MATLAB提供了在有限区间内近似计算某函数的定积分的函数，它们分别是cumsum（矩形方法求积分），trapz（梯形方法求积分），quad（辛普森方法求积分），quad8（科茨方法求积分）．

A．矩形法求数值积分

矩形法数值积分用函数cumsum来实现．对于向量x，cumsum（x）返回一个向量，其第i个元素为向量x的前i个元素的和．

例：利用矩形法计算积分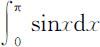 （精确值为2）．

>>x＝linspace（0，pi，100）；％在［0，π ］之间取100个离散点

>>y＝sin（x）；

>>T＝cumsum（y）*pi/（100-1）；％pi/（100-1）表示步长

>>I＝T（100）％函数在［0，π ］之间的矩形积分

B．梯形法求数值积分

z＝trapz（x，y）表示通过梯形积分法计算y对x的数值积分．x和y必须是长度相等的向量．

例：利用梯形法计算积分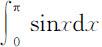 （精确值为2）．

>>x＝linspace（0，pi，100）；

>>y＝sin（x）；

>>t＝trapz（x，y）

C．辛普森（simpson）法求数值积分

辛普森法数值积分用函数quad来实现，quad函数的调用格式如下：

q＝quad（′f′，a，b）

q＝quad（′f′，a，b，tol）积分的误差在tol范围内．

D．科茨（cotes）法求数值积分

（1）q＝quadl（fun，a，b）

（2）q＝quadl（fun，a，b，tol）

【例】

>>q＝quad（′sin′，0，pi）％用simpson求sinx在［0，pi］的积分

>>z＝quadl（′exp（-x·2）′，-1，1）％用cotes求积分