表2.2　水质污染综合排序

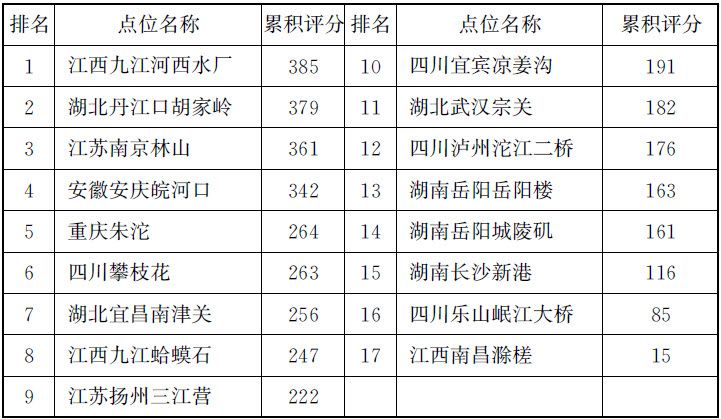
（二）问题2的建模与求解

（1）模型的建立

某一污染物扩散所满足的微分方程是一个抛物线方程，结合实际问题的假设，常可假定其水流近似地处于稳定状态，断面沿程均匀．普通对流扩散方程为

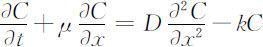
其中，μ 表示断面平均流速， ．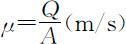

上式是解决污染物浓度的一般原理，结合问题2的实际情况，进行进一步的分析．假设观测站干流的污染物浓度在一个月内保持稳定，则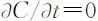： ．又弥散系数D 是分子热运动造成污染物扩散的程度大小，它相对于江河流速μ 来说是微不足道的，可以忽略不计，即：D ＝0．所以上式进一步简化为

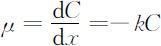
其中，C 为某组分子在x 断面的浓度；k 为降解常数．由此求出长江干流污染物浓度C_x 与距观测站长度x 米的函数关系为

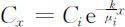
在距离上游为L_i 处时河水浓度为

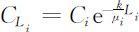
由于排污口的位置难以确定，为方便处理，现假设排污口位于第i 段干流的下游某处，结合上式，可得下游排污口排污浓度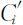为 ，方程为

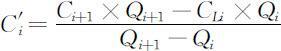
又假设排污口位于第i 江段的上游，其排污浓度为

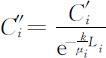
把排污口位于上游或位于下游不同情况下的平均单位时间排污量，平均取值作为此江段上的排污量．由常识，在下一站点浓度不变时，排污口位于上游的排污量显然高于排污口位于下游的排污量，并依次作为衡量排污量多少的指标．

综上所述，长江第i 段干流的污染物平均单位时间的排放量（毫克／秒）为

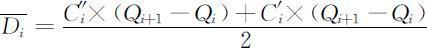
（2）模型的求解结果

对于一维单河段水质模型，两种污染物浓度相对较高的河段就是高锰酸盐指数和氨氮的污染源主要所在地区．利用Matlab软件求解得：长江干流一年多来主要污染物高锰酸盐指数的污染源主要在湖北宜昌到湖南岳阳段、江西九江到安徽安庆段．氨氮的污染源主要在湖北宜昌到湖南岳阳段、湖南岳阳到江西九江段．