2.4　微分方程建模案例分析2

例4　SARS的传播 （CUMCM 2003年A题）

在全国大学生高教社杯数学建模竞赛2003年的A题中，描述SARS病毒被传染人数增加的传播规律，可以采用微分差分方程组合模型．将整个社会看成一个系统，重点考虑研究对象是否已退出系统．对于处于系统中的各种参量间的关系体现在模型中．

用N （t ）描述在某时刻此传染系统内的总人口数；γ 描述自由传播源平均每天造成的感染率；μ 描述平均每天的治愈率；δ 为患者平均每天的死亡率；t ₀ 是当疫情蔓延到一定程度后，政府等机构采取措施的起始时间（即控制起始时间）；M （t ）描述过了潜伏期，表现出症状，但还未隔离的患者数（自由传染源）；I （t ）为t 时刻传染源的总数；DP （t ）为t 时刻疑似病例的人数；CP （t ）为t 时刻确诊病人的人数；R （t ）为t 时刻的退出传染系统的人数（包括康复者［据资料不会再次感染］、死亡者）；S （t ）为t 时刻的健康人数（易感染人群，不包括患病后治愈的）；用β ₁ 表示疑似病例中每日被排除的人数占疑似病例的比例；β ₂ 表示为疑似病例中每日转化为确诊病人占疑似病例的比例；α 表示为被自由传染源有效感染的人中的可控系数．

据资料，SARS潜伏期的患者不具有传染性，则：I （t ）＝M （t ），模型为：

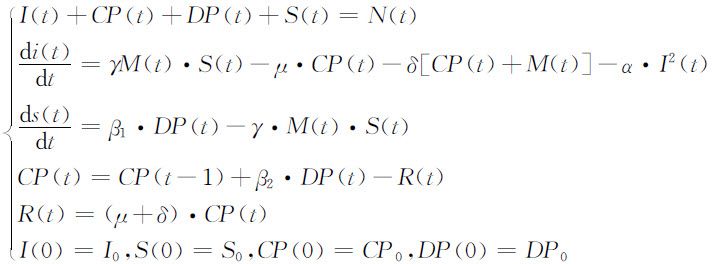
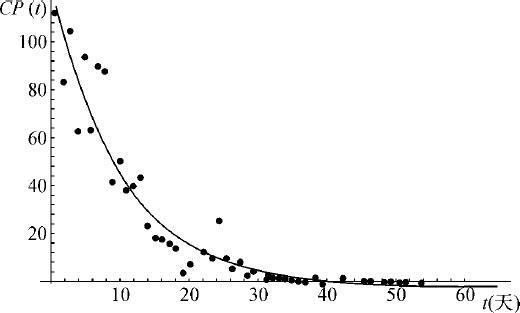
对题中的数据去除偏离较大的点，进行多项拟合，得：β ₁ ，β ₂ ，及μ ＋δ ，并且通过前10天的实际数据，做出时间的函数图象，用计算机在领域内以微小步长搜索，并不断调整使理论图象与实际图象尽量趋于一致，得到此时的γ ＝0.532；α ＝0.683．由于I （t ）的数值解没有原始数据与之做对比，我们转化为作10天以后的“确诊病例日增量图”，见图2.14．可见，总体趋势符合得很好，但个别点有较大的误差．