4.3　线性回归分析方法

4.3.1　线性回归模型及其矩阵表示

一般而言，某个随机变量Y往往相关于另外一些变量X 1 ，X 2 ，…，X p -1 ，但这种相关关系或者由于其机理不甚明确，或者由于问题的复杂性而不能确切知道，因此只能说由X 1 ，X 2 ，…，Xp 的取值部分地决定Y 的取值．如某种商品的销量Y 与众多的社会经济学和人口统计学变量如消费者年龄X 1 、性别X 2 、经济收入X 3 以及商品的价格X 4 等有关，同样，由这些变量的取值不能完全决定该商品的销量．在这些情况下，我们可以认为Y 的值由两部分构成，一部分是由X 1 ，X 2 ，…，X p -1 能够决定的部分，它是X 1 ，X 2 ，…，X p -1 的某个函数，记为函数f （X 1 ，X 2 ，…，X p -1 ）；另一部分是众多未加考虑的因素（包括随机因素）所产生的影响，被看作是随机误差，记为ε ．于是Y 与X 1 ，X 2 ，…，X p -1 的关系可表示为

4.3 线性回归分析方法 - 图1

回归分析即是利用Y 与X 1 ，X 2 ，…，X p -1 的观测数据，并在误差项的某些假定下确定f （X 1 ，X 2 ，…，X p -1 ）．利用统计推断方法对所确定的函数的合理性以及由此关系所揭示的Y 与各X 1 ，X 2 ，…，X p -1 的关系作分析，进一步应用于预测、控制等问题．

特别，当f （X 1 ，X 2 ，…，X p -1 ）为X 1 ，X 2 ，…，X p -1 线性函数时，我们有

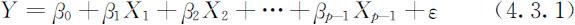
4.3 线性回归分析方法 - 图2

称此模型为线性回归模型，它是变量间相关性建模研究的基本模型，其中β 0 ，β 1 ，…，β p -1 是未知常数，称为回归参数或回归系数；Y 称为因变量或响应变量；X 1 ，X 2 ，…，X p -1 称为自变量或回归变量；ε 称为随机误差项，并假定E （ε ）＝0．ε 是不可观测的随机变量，而Y 和X 1 ，X 2 ，…，X p -1 是可观测的变量，本章只讨论变量X 1 ，X 2 ，…，X p -1 是非随机变量的情形，而Y 是与ε 有关的随机变量，它是可观测的．

这里需要指出的是线性回归分析就其分析方法的本质上看并不要求Y 与X 1 ，X 2 ，…X p -1 之间呈线性关系，而只要求Y 与未知参数β 0 ，β 1 ，…，β p -1 ，具有线性关系即可．在此意义上，一个最一般的线性回归模型为

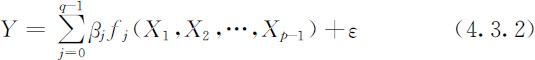
4.3 线性回归分析方法 - 图3

其中fj （X 1 ，X 2 ，…，X p -1 ），j ＝0，1，…，q -1是q 个线性无关的已知函数，这时只要设置新的变量

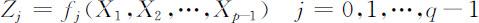
4.3 线性回归分析方法 - 图4

便可将模型（4.3.2）化为线性回归模型，通过fj （X 1 ，X 2 ，…，X p -1 ），j ＝0，1，…，q -1的不同形式，模型（4.3.2）包含了十分广泛的一类回归模型．特别地，若取q ＝p ，函数f 0 （x 1 ，x 2 ，…，x p -1 ）＝1，函数fj （X 1 ，X 2 ，…，X p -1 ）＝Xj ，j ＝0，1，…，q -1，则模型（4.3.2）便是标准的线性回归模型（4.3.1）．因此，本章主要研究模型（4.3.1），而其方法适合于一般线性回归模型（4.3.2）．

为建立线性回归模型（4.3.1），我们对Y，X 1 ，X 2 ，…，X p -1 进行n （n ⩾p -1）次独立观测，得n 组观测值（称为样本数据）

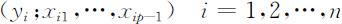
4.3 线性回归分析方法 - 图5

它们满足关系式

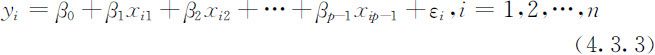
4.3 线性回归分析方法 - 图6

利用矩阵记号，令

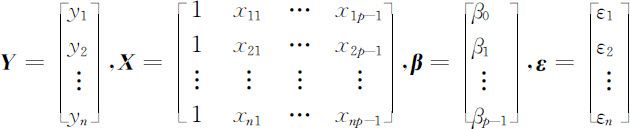
4.3 线性回归分析方法 - 图7

则（4.3.3）式可写为

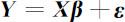
4.3 线性回归分析方法 - 图8

称此为线性回归模型的矩阵形式，其中 Y 称为观测向量； X 称为设计矩阵，并假定它是列满秩的，即rank（X）＝p ． Y 和 X 由样本数据所决定，是已知的． β 是待估计的回归参数向量； ε 是不可观测的随机误差向量，本章中恒假定其各分量相互独立，均服从均值为零，方差σ 2 的正态分布，即 ε ～N （0 ， σ 2 I ）．

建立回归模型的第一步是利用观测数据对回归参数β 做出估计，一般我们采用最小二乘法进行参数估计．β 的最小二乘估计即选择β 使得误差项的平方和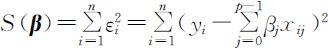4.3 线性回归分析方法 - 图9 达到最小，记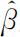4.3 线性回归分析方法 - 图10 为β 的最小二乘估计值，于是，可以得到回归方程：

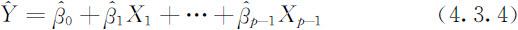
4.3 线性回归分析方法 - 图11

4.3.2　回归方程的显著性检验

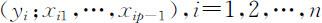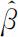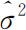对于线性回归模型（4.3.1），利用因变量Y 与自变量x 1 ，x 2 ，…，x p -1 的n 组观测数据4.3 线性回归分析方法 - 图12 可以得到未知参数β 和σ 2 的估计4.3 线性回归分析方法 - 图13 和4.3 线性回归分析方法 - 图14 ，从而可得到回归方程（4.3.4），并以此可根据自变量的观测值对Y 的取值作预测．但Y 与X 1 ，X 2 ，…，X p -1 之间的线性关系的假定有很大的主观性，所求得的回归方程是否有意义，也就是说Y 与X 1 ，X 2 ，…，X p -1 之间是否存在显著的线性关系，还需要对所建立的回归方程作进一步统计检验．

4.3.3　回归系数的统计推断

前述线性回归关系的显著性检验是对回归方程的一个整体性检验．如果检验结果是拒绝原假设H 0 ，则意味着Y 显著地相关于X 1 ，X 2 ，…，X p -1 的线性函数这个整体，但这并不意味着每个自变量Xk ，（1⩽k ⩽p -1）均通过其线性函数对Y 产生显著影响．也就是说，自变量中的某些对Y 的影响可能不显著，其极端情形就是某些回归系数βk 会等于零．因此，在线性回归关系检验中，若H 0 被拒绝，我们还需要对每个自变量逐一作显著性检验，即对固定的k （1⩽k ⩽p-1），检验假设

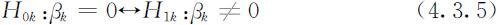
4.3 线性回归分析方法 - 图15

下面我们基于βk 的最小二乘估计构造适当的统计量检验上述假设．

由最小二乘估计方法，β 的最小二乘估计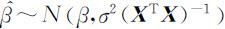4.3 线性回归分析方法 - 图16 ．设ckk 为（ X T X ）-1 的主对角线上的第k 个元素，则有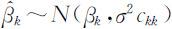4.3 线性回归分析方法 - 图17 从而

4.3 线性回归分析方法 - 图18

又由概率统计知识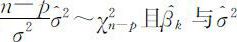，4.3 线性回归分析方法 - 图19 相互独立，因此有

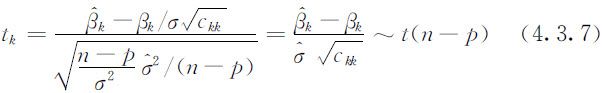
4.3 线性回归分析方法 - 图20

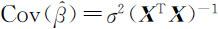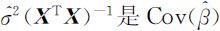其中t （n-p ）表示自由度为n-p 的t 分布，同时也表示服从自由度为n-p 的t 分布的随机变量．进一步，因为4.3 线性回归分析方法 - 图21 ，因此4.3 线性回归分析方法 - 图22 的一个很自然的估计．由此可知，（4.3.6）式中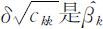4.3 线性回归分析方法 - 图23 的标准差的估计，它是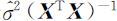4.3 线性回归分析方法 - 图24 的主对角线上的第k 个元素的算术平方根，记此估计为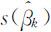4.3 线性回归分析方法 - 图25 ．于是（4.3.7）式变为

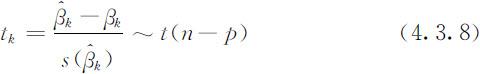
4.3 线性回归分析方法 - 图26

特别当H 0k 为真时，有

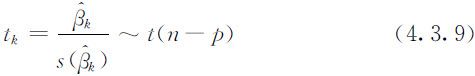
4.3 线性回归分析方法 - 图27

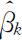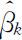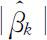这时4.3 线性回归分析方法 - 图28 作为4.3 线性回归分析方法 - 图29 的无偏估计，4.3 线性回归分析方法 - 图30 的值不应过分偏大，即|tk |的值不应过分偏大．否则，若H 1k 为真，则|tk |有偏大的趋势．设|t 0k |为样本数据通过（4.3.8）式所求得的统计量|tk |的观测值，则检验假设（4.3.5）的p 值为

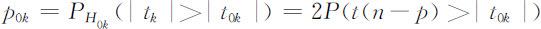
4.3 线性回归分析方法 - 图31

对于给定的显著水平x ，若p 0k <α ，则拒绝H 0k ，认为xk 对于Y 的影响显著；否则不能拒绝H 0k ，认为xk 对于Y 的影响不显著．

另一方面，利用（4.3.9）式可以给出βk 的置信度为1-α 的置信区间，我们将其简记为

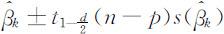
4.3 线性回归分析方法 - 图32

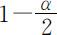其中4.3 线性回归分析方法 - 图33 表示自由度为n-p 的t 分布的（下侧）4.3 线性回归分析方法 - 图34 分位数．

4.3.4　剔除变量的计算

在实际问题中，可能会有一个或几个变量在回归方程中不起作用，就应该从回归方程中剔除掉影响不显著的变量，重新建立只包含线性影响显著的变量的回归方程，以便更好地进行预测与控制．当有几个变量为不显著变量时，我们不能将这些变量都一次性剔除，因为变量之间具有相关性，每次只能将其中最不显著的变量即|tk |值最小的变量Xk 剔除，然后重新建立减少变量Xk 后的回归方程，再对新建立的回归方程的回归系数逐一检验，若还有不显著变量再剔除一个，再重新建立回归方程，直到回归方程中的变量都显著为止．

4.3.5　预测及统计推断

利用回归方程除了对Y 与自变量X 1 ，X 2 ，…，X p -1 的相关关系作分析，了解各自变量对Y 的影响的显著性以外，另一个重要的应用就是对因变量取值的预测．假设已由样本（x i 1 ，x i 2 ，…，x ip -1 ）（i ＝1，2，…，n ）计算得到回归方程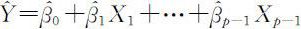4.3 线性回归分析方法 - 图35 ，经检验，回归效果以及各回归系数都是显著的．在给定一组值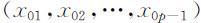4.3 线性回归分析方法 - 图36 ，则可求出y 0 的点估计以及预测区间．

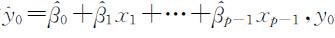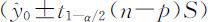y 0 的点估计为4.3 线性回归分析方法 - 图37 的置信度为1-α 的预测区间（置信区间）为：4.3 线性回归分析方法 - 图38 ．