2.3　微分方程建模案例分析1

本节针对实际问题，在对其具体情况进行分析或类比后，给出相应的假设条件，建立对应的数学模型，利用合适的数学工具对模型进行求解，对结果进行检验．

例1 　随着卫生设施的改善，医疗水平的提高以及人类文明的不断发展，诸如霍乱、天花等曾经肆虐全球的传染性疾病已经得到有效的控制．但是一些新的、不断变异的传染病毒却悄悄向人类袭来.20世纪80年代十分险恶的艾滋病毒开始肆虐全球，至今仍在蔓延；2003年春，来历不明的SARS病毒突袭人间，给人们的生命财产带来了极大的危害．长期以来，建立传染病的数学模型来描述传染病的传播过程，分析受感染人数的变化规律，探索制止传染病蔓延的手段等，一直是各国有关专家和官员关注的课题．

不同类型传染病的传播过程有其各自不同的特点，弄清这些特点需要相当多的病理知识，本节不从医学的角度分析各种传染病的传播，而只是按照一般的传播机理建立4种模型．

一、模型Ⅰ

和人口模型中的指数模型一样，可以假设时刻t 的病人人数x （t ）是连续、可微函数，并且每天每个病人有效接触（足以使人致病的接触）的人数为常数λ ，考察t 到t ＋Δt 时间段内病人人数的增加，就有：

令Δt →0，得到x （t ）满足方程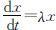： ，再设当t ＝0时，有x ₀ 个病人，可以得到微分方程：

利用分离变量法容易得到方程的解为：

结果表明，随着t的增加，病人人数x （t ）无限增长，这显然是不符合实际的．

建模失败的原因在于：在病人有效接触的人群中，有健康人也有病人，而其中只有健康人才可以被传染为病人，所以在改进的模型中必须区别这两种人．

二、模型Ⅱ（SI模型）

假设条件为：

1．在疾病传播期内该考察地区的总人数N 不变，既不考虑生死，也不考虑迁移．人群分为易感染者（Susceptible）和已感染者（Infective）两类（取两个词的第一个字母，称之为SI模型），以下简称健康者和病人．时刻t 这两类人在总人数中所占的比例分别记作s （t ）和i （t ）．

2．每个病人每天有效接触的平均人数是常数λ，λ 称为日接触率．当病人与健康者有效接触时，使健康者受感染变为病人．

根据假设，每个病人每天可使λs （t ）个健康者变为病人，由于病人数为Ni （t ），所以每天共有λNs （t ）i （t ）个健康者被感染，考察t 到t ＋Δt 病人人数的增加有：

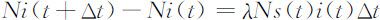
令Δt →0，得：

又考虑到：

再记初始时刻（即t ＝0）病人的比例为i ₀ ，则得微分方程：

利用分离变量法容易得到方程的解为：

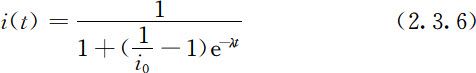
i （t ）-t 和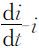 的图形如图2.1和图2.2所示．

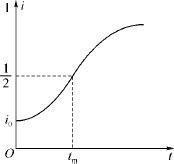
图2.1　SI模型的i-t 曲线

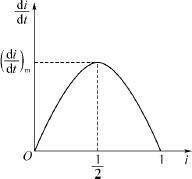
图2.2　SI模型的di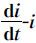 曲线

由（2.3.5）式、（2.3.6）式及图2.1可知：第一，当i ＝0.5时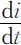 达到最大值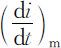 ，这个时刻为：

此时，病人数增加得最快，可以认为是医院的门诊量最大的一天，预示着传染病高潮的到来，是医疗卫生部门关注的时刻．t_m 与λ 成反比，因为日接触率λ 表示该地区的卫生水平，λ 越小卫生水平越高．所以改善保健设施、提高卫生水平可以推迟传染病高潮时刻的到来．第二，当t →∞时i →1，即所有人终将被感染，全变为病人，这显然不符合实际情况．其原因是模型中没有考虑到病人可以治愈，人群中的健康者只能变成病人，病人不会再变成健康者．

为了修正上述结果，必须重新考虑模型的假设条件，下面两个模型讨论的是病人可以治愈的情况．在可以治愈的情形下，有的传染病（如伤风、痢疾等）愈合后免疫力很低，可以假定无免疫性，这个问题在模型Ⅲ中讨论，在该模型中病人被治愈后变成健康者，健康者还可以被再次感染变成病人，所以该模型也称为SIS模型．而有的传染病（如天花、流感、肝炎、麻疹等）治愈后均有很强的免疫力，所以病愈的人既非健康者（易感染者），也非病人（已感染者），他们已经退出传染系统，把他们叫做移出者（R emoved），所以该模型也称为SIR模型．下面对这两种模型进行详细的介绍．

三、模型Ⅲ（SIS模型）

在SI模型假设的基础上，要增加一个条件．

3．每天被治愈的病人数占病人总数的比例为常数μ ，称为日治愈率．病人治愈后成为仍可被感染的健康者．显然1／μ 是这种传染病的平均传染期．

不难看出，考虑到假设3，SI模型应修正为：

（2.3.4）式不变，于是（2.3.5）式应改为：

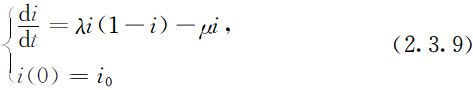
利用分离变量法可求出（2.3.9）式的解析解，为：

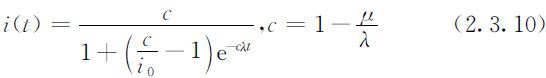
通过图形来分析i （t ）的变化率．定义

注意到λ 和 的含义，可知σ 就是整个传染期内每个病人有效接触的平均人数，称为接触数．

利用（2.3.9）式和（2.3.10）式，容易画出i （t ）-t 和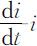 的图形，见图2.3～图2.6所示．

图2.3　SIS模型的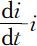 曲线（σ >1）

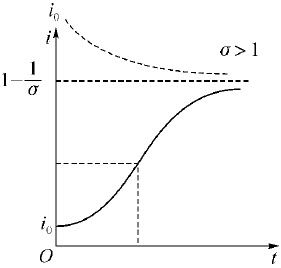
图2.4　SIS模型的i （t ）-t 曲线（σ >1）

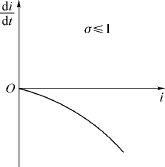
图2.5　SIS模型的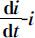 曲线（σ ⩽1）

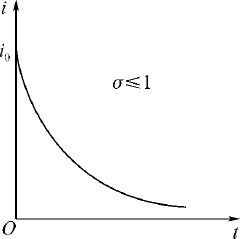
图2.6　SIS模型的i （t ）-t 曲线（σ ⩽1）

不难看出，接触数σ ＝1是一个阈值．当σ >1时，i （t ）的增减性取决于i ₀ 的大小（见图2.4），但其极限值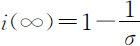 随σ 的增加而增加，这说明，接触数σ 越大（当地的医疗水平越低），整个被传染的人数就越大，这与实际是吻合的．当σ ⩽1时，i （t ）越来越小，最终趋于零，这是因为传染期内经有效接触的人数不超过原来病人数的缘故．模型较好地解释了传染病传播的规律．

当μ →0时，SIS模型就是SI模型，说明SI模型是它的特例．

四、模型Ⅳ（SIR模型）

由于有些传染病病人被治愈后会有免疫力，所以这部分人，既不是易感染者，也不是已感染者，他们已经退出了传染系统，所以我们应该对这部分人进行考虑．

1．模型假设

SI模型的假设可以修改成如下形式：

（1）总人数N 不变．人群分为健康者、病人和移出者三类，他们在总人数N 中所占比例分别记作s （t ），i （t ）和r （t ）．

（2）病人的日接触率为λ ，日治愈率为μ ，传染期接触数为σ ＝λ ／μ ．

（3）设初始时刻的健康者和病人的比例分别是s ₀ （>0）和i ₀ （>0），移出者的初始值为r ₀ ．

2．模型构成

由第一个假设容易有：

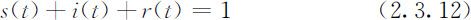
由于这里仍然考虑病人会被治愈的情况，故（2.3.8）式仍成立．而对于病愈后具有免疫力的移出者而言，应该有：

那么，由（2.3.8）式，（2.3.12）式和（2.3.13）式，SIR模型的方程可以写作：

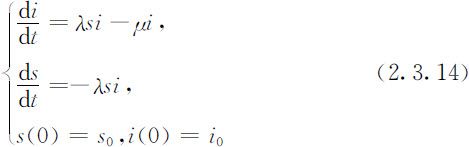
（2.3.14）式为常微分方程组，但此时无法求出s （t ）和i （t ）的解析解，于是考虑利用数学工具（如Matlab软件）求其数值解．

3．模型求解

在方程（2.3.14）式中设λ ＝1，μ ＝0.3，i （0）＝0.02，s （0）＝0.98，用Matlab软件编程．有两个M文件，一个是ill.m，一个是主程序SIR.m．其中ill.m的语句为：

Function y＝ill（t，x）

a＝1；

b＝0.3；

y＝［ax（1）x（2）－bx（1），－ax（1）*x（2）］’；

它是一个函数文档，以关键词function开头，函数的名称是ill，与M文件的名称保持一致．其中保存的是常微分方程组的函数，并以变量名y （为一数组）返回．

主程序SIR.m中对变量（s ₀ ，i ₀ ，t ）赋初值，并利用Matlab软件中自带的函数ode45求解微分方程组，计算s （t ），i （t ）在时间t 上的函数值，并画图．语句为：

ts＝0∶50；

x0＝［0.02，0.98］；

［t，x］＝ode45（‘ill’，ts，x0）

plot（t，x（：，1），t，x（：，2）），grid，pause

plot（x（：，2），x（：，1）），grid

输出的简明计算结果列入表2.1，i （t ），s （t ）的图形见图2.7，i （t ）-s （t ）的图形见图2.8，图中曲线称为相轨线，初值i （0）＝0.02，s （0）＝0.98相当于图2.8中的P ₀ 点，随着t 的增加，（s，i ）沿轨线自右向左运动．当t ＝7时，i （t ）达到最大值，然后减少，t →∞，i →0；而s （t ）则单调减少，t →∞，s →0.0398．

表2.1　i （t ），s （t ）的数值计算结果

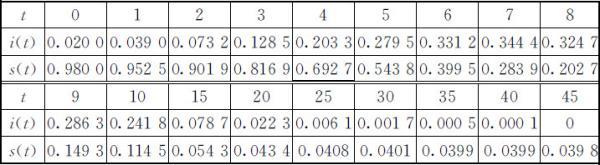
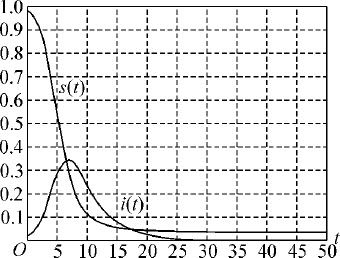
图2.7　i （t ），s （t ）图形

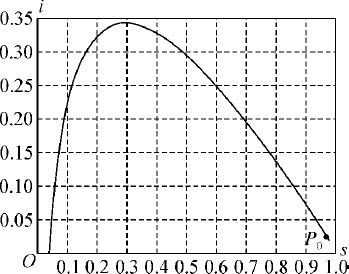
图2.8　i （t ）-s （t ）图形（相轨线）

4．结论分析

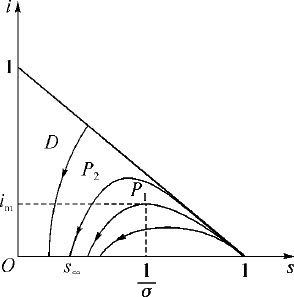
为了分析i （t ），s （t ）的一般变化规律，需要进行相轨线分析．s-i 平面称为相平面，相轨线在相平面上的定义域D 为：

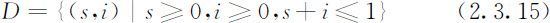
在方程（2.3.14）中消去dt 并注意到σ 的定义，容易得到：

（2.3.16）式的解容易得到：

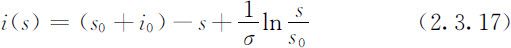
在定义域D 内，（2.3.17）式表示的曲线即为相轨线，如图2.9所示．其中箭头表示了随着时间t 的增加s （t ）和i （t ）的变化趋向．