4.1　数据分布拟合方法基础

4.1.1　数据描述性分析的数字特征

数据的描述性分析就是从数据出发概括数据特性，主要包括数据的位置特性、分散性、关联性等数字特征和反映数据整体结构的分布特征，它是数据分析的第一步，也是对数据进行更进一步分析的基础．

4.1.1.1　一维数据的数字特征

设有n 个一维数据：x ₁ ，x ₂ ，…，x_n ．它们是从总体X中观测得到的一个样本．其从小到大的顺序统计量值为x _（1） ，x _（2） ，…，x _{（n ）} ．在数学建模实践中，常用的描述一维数据的数字特征的随机变量主要有：

一、表示位置的数字特征

1．均值：

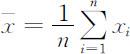
2．中位数：

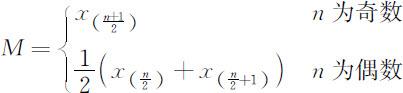
3．分位数：

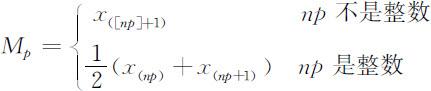
其中0⩽p<1，［np ］表示np 的整数部分．当p ＝1时，定义：M ₁ ＝x _{（n ）} ．

二、表示分散性的数字特征

1．标准差：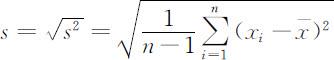

2．变异系数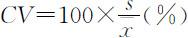： ，它为一个无量纲的值．

3．极差：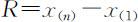

三、表示分布形状的数字特征

1．偏度：

其中s 为标准差，偏度是刻画数据分布对称性的指标．

若g ₁ ≈0，则认为数据分布是近似对称的；

若g ₁ >0，则认为数据是右偏态的；

若g ₁ <0，则认为数据是左偏态的．

2．峰度：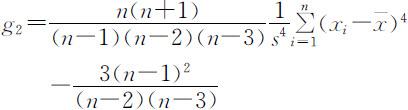

峰度是另一种度量分布形状的量，它是以正态分布为标准，比较两侧极端数据分布情况的指标．当数据的总体分布为正态分布时，峰度g ₂ ≈0；若g ₂ >0，表示数据中含有较多远离均值的极端数值；若g ₂ <0表示均值两侧的极端数值较少．

4.1.2　数据的参数分布类型

在数学建模中，我们经常需要对所研究的总体中所抽取的样本数据进行分布拟合检验，了解一些常见的数据参数分布类型是必要的．下面我们给出几类建模中经常用到的随机变量的概率密度函数，详细的介绍可参见《数据分析方法》或者其他的数理统计文献．

1．正态分布的概率密度函数：

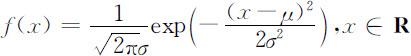
2．对数正态分布的概率密度函数：

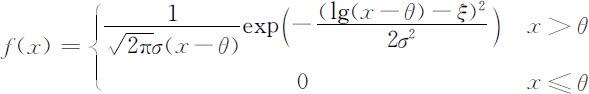
3．指数分布：

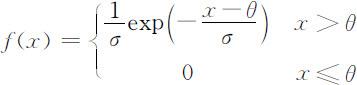
4．Gamma分布：

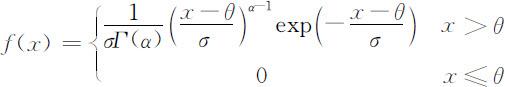
5．Weibull分布：

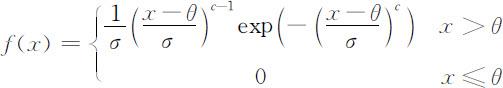
6．Beta分布：

4.1.3　数据的分布拟合检验方法

在许多实际问题的数学建模中，总体的分布类型往往不知道，或者知之甚少，这就需要根据样本的观察值对总体分布的类型及其参数进行统计推断，这就是我们所说的分布拟合检验问题．

1．皮尔逊（K．Pearson）χ ² 检验方法

皮尔逊χ ² 检验法是著名的英国统计学家K．Pearson于1900年提出来的．下面我们介绍这一方法．

设总体X 的分布未知，根据样本X ₁ ，X ₂ ，…，X_n 来检验关于总体分布的假设．假设检验问题为：

H ₀ ：总体X 的分布函数为F ₀ （x ）

H ₁ ：总体X 的分布不是F ₀ （x ）

皮尔逊χ ² 检验法的基本思想如下：在对数据按其取值范围进行分组后计算频数的基础上，考察每个区间的实际频数与理论频数的差异，它使用如下的χ ² 统计量：

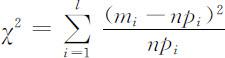
其中n 是样本观测数据的容量，l 是分组数，m_i 和p_i 分别为样本观测值落入第i 组的频数与其理论频数，第i 组的概率，其值可根据原假设所指定的分布求得．

根据假设检验问题：

将实轴分为l 个区间，分点满足

得l 个区间

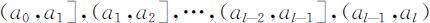
设p_i 是原假设H ₀ 为真时，服从F ₀ （x ）的随机变量取值于第i 个区间（a _{i -1} ，a_i ］的概率，即

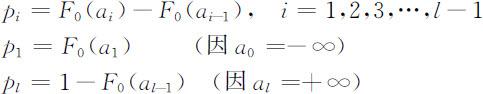
从而得到检验统计量χ ² ．设k 是F ₀ （x ）中待估参数的个数，例如，原假设是正态分布，其中均值μ 与方差σ ² 待估计，此时k ＝2．可证明当样本容量n 充分大且原假设H ₀ 为真时，统计量近似服从自由度为l-k -1的χ ² 的分布，即

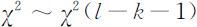
若原假设H ₀ 为真，χ ² 的值应比较小；否则，χ ² 有偏大的趋势．故对给定的显著水平α ，设由样本观测值算得的χ ² 的观测值是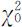 ，则当 时，拒绝H ₀ ；否则，不能拒绝H ₀ ．这里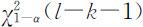， 表示自由度为l-k -1的χ ² 分布的（下侧）分位数．

2．正态性W 检验法

W 检验法是夏皮罗（S．S．Shapiro）与威尔克（M．B．Wilk）于1965年提出的一种灵敏度高，计算简单，需要的样本容量小的正态性检验方法．W 统计量的计算步骤如下．

设样本观测值为x ₁ ，x ₂ ，…，x_n ，其次序统计量为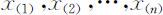 ．计算

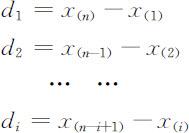
当n 是偶数时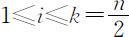， ；当n 是奇数时， ，将d_i 与系数a_i （有表可查）相乘并求和，得

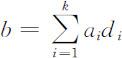
计算

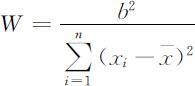
W 统计量满足0<W ⩽1，假设检验问题为

H ₀ ：F （x ）是正态分布函数，H ₁ ：F （x ）不是正态分布函数

在原假设H ₀ 为真时，W 的值接近于1，W 的值过小应拒绝H ₀ ，因此其检验p 值为

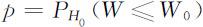
其中W 是根据样本观测值x ₁ ，x ₂ ，…，x_n 算得的W ．当p <α 时，拒绝H ₀ ；当p ⩾α 时，不能拒绝H ₀ ．

4.1.4　多维数据的数字特征及相关分析

在实际生活中，人们更多遇到的是多维数据，它是从多维总体（X ₁ ，x ₂ ，…，x_p ）^T （p 维）中观测得到的．对于多维数据，除按前述一维数据的描述性分析方法分析各分量取值的数字特征外，更重要的是分析各个分量之间的相关关系，这就是多维数据的相关分析．

1．相关系数

设（X，Y ）^T 是二维总体，从中得到观测数据（x_i ，y_i ）^T ，i ＝1，2，…，n ．引进数据观测矩阵

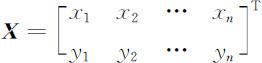
记

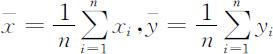
则（X，Y ）^T 称为二维观测数据的均值向量．记

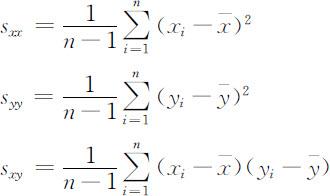
分别称s_xx 和s_yy 为X，Y 的观测数据的方差，称s_xy 为X，Y 的观测数据的协方差，而

称为观测数据的协方差矩阵．注意总有s_xy ＝s_yx ，即数据的协方差矩阵是对称矩阵．

由Schwarz不等式有：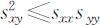

所以 S 总是非负定的．观测数据的相关系数计算公式是

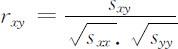
由Schwarz不等式，有|r_xy |⩽1，称r_xy 为Pearson相关系数．

2．多维数据的Pearson相关矩阵

设（X ₁ ，X ₂ ，…，X_p ）^T 是p 维总体，从中取得样本数据

记各组观测数据为

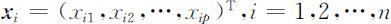
称之为样品，引进n ×p 样本数据观测矩阵

X 的p 个列分别是p 个变量 X ₁ ， X ₂ ，…， X _p 的n 个观测数据．

（1）第j 列数据的均值

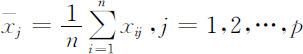
（2）第j 列数据的方差

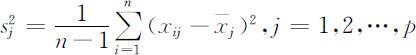
（3）第j，k 列数据的协方差

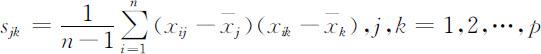
并且有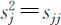

称

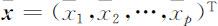
为p 维样本观测数据的均值向量．称

为样本观测数据的协方差矩阵．易知有

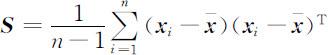
均值向量 x 与协方差矩阵 S 是p 维观测数据的重要数字特征． x 表示p 维观测数据的集中位置，而协方差矩阵 S 的对角线元素分别是各个变量观测值的方差，非对角线元素是两两变量观测值之间的协方差．

（4） X 的第j，k 列数据的相关系数

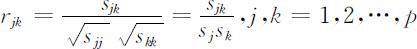
r_jk 是无量纲的量，总有 ．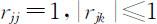

称

是观测数据的Pearson相关矩阵．记

对p 阶对角矩阵，则有

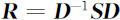
相关矩阵 R 也是p 维观测数据的最重要的数字特征，它刻画了变量观测值之间的线性相关的密切程度． R 往往是多维数据分析的出发点． S 及 R 总是非负定的，在实际应用中， S 及 R 常是正定的．

观测数据矩阵 X 的第j，k 列数据的Spearson相关系数记为q_jk ，称

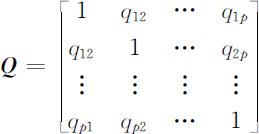
为多维数据的Spearson相关矩阵．从其定义看，数据的Spearson相关矩阵视乎较Pearson相关矩阵损失了数据的某些信息，但Spearson相关矩阵适用于研究具有一般分布的p 维总体，且对有异常值的观测数据，具有耐抗性． Q 同样是非负定的．