6.4　模糊综合评价

在客观世界中，存在大量的模糊概念和模糊现象，模糊数学就是试图用数学工具解决模糊事物方面的问题．模糊综合评价方法是模糊数学中应用比较广泛的一种方法．模糊综合评价是以模糊数学为基础，应用模糊关系合成的原理，将一些边界不清，不易定量的因素定量化，进行综合评价的一种方法．它具有结果清晰、系统性强的特点，能较好地解决模糊的、难以量化的问题，适合各种非确定性问题的解决．模糊综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价，即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价．模糊综合评价的基本思想是：许多事情的边界并不十分明显，评价时很难将其归于某个类别，于是我们先对单个因素进行评价，然后对所有因素进行综合模糊评价，防止遗漏任何统计信息和信息的中途损失，这有助于解决用“是”或“否”这样的确定性评价带来的对客观真实的偏离问题．

6.4.1　模糊综合评价法

模糊综合评价法的基本原理是：首先确定被评价对象的因素（指标）集合评价（等级）集，再分别确定各个因素的权重及它们的隶属度向量，获得模糊评判矩阵，最后，把模糊评判矩阵与因素的权向量进行模糊运算并进行归一化，得到模糊综合评价结果．

6.4.2　模糊综合评价的模型与步骤

设评判对象为P

1．确定评价对象的因素论域：设评判对象的因素集记为：U ＝｛u ₁ ，u ₂ ，…，u_n ｝，也就是说评判对象有n 个指标，表明我们对评价对象从哪些方面进行评判描述．

2．确定评语等级论域：评语集是评价者对被评价对象可能做出的各种总的评价结果组成的集合，评判等级集记为：V ＝｛v ₁ ，v ₂ ，…，v_n ｝．评语集实际上就是对被评价对象变化区间的一个划分，其中，v_i 表示第i 个评价结果，n 为总的评价结果数．具体等级可以依据评价内容用适当的语言进行描述，比如评价产品的竞争力可用V ＝｛强、中、强｝，评价某地区的社会经济发展水平可用V ＝｛高、较高、一般、较低、低｝等．

3．进行单因素评价、建立模糊关系矩阵

单独从一个因素出发进行评价，以确定评价对象对评价集合V 的隶属程度，称为单因素模糊评价．在构造了等级模糊子集后，要逐个对被评事物从每个因素u_i （i ＝1，2，…，p ）上进行量化，即确定从单因素来看被评事物对等级模糊子集的隶属度（R |u_i ），进而得到模糊关系矩阵：

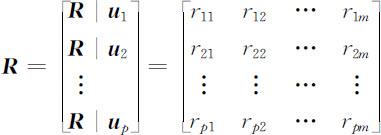
矩阵 R 中第i 行第j 列元素r_ij ，表示某个被评事物从因素u_i 来看对v_j 等级模糊子集的隶属度．一个被评事物在某个因素u_i 方面的表现，是通过模糊向量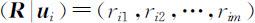 来刻画的，而在其他评价方法中多是由一个指标实际值来刻画的，因此，从这个角度讲模糊综合评价要求更多的信息．在确定隶属关系时，通常由专家或与评价问题相关的专业人员，依据评判等级对评价对象进行打分，然后统计打分结果，然后根据绝对值减数法求得r_ij ，即：

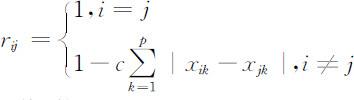
其中，c 可以适当取值，使0⩽r_ij ⩽1．

4．确定评价因素的模糊权向量

在模糊综合评价中，确定评价因素的权向量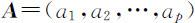： ．权向量 A 中的元素a_i 本质上是因素u_i 对模糊子｛对被评事物重要的因素｝的隶属度．通常a_i 满足

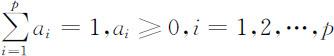
它表示第i 个因素的权重，再由各权重组成的一个模糊集合A 就是权重集．在进行模糊综合评价时，权重对最终的评价结果会产生很大的影响，不同的权重有时会得到完全不同的结论．权重选择的恰当与否关系到模型的成败，常用的确定权重的方法有：层次分析法、Delphi法、加权平均法、专家估计法等．

5．合成模糊综合评价向量

利用合适的算子将与各被评事物的进行合成，得到各被评事物的模糊综合评价结果向量 B ．即

其中b_j 是由 A 与 R 的第j 列运算得到的，它表示被评事物从整体上看对v_j 等级模糊子集的隶属程度．

6．对模糊综合评价结果向量进行分析

模糊综合评价的结果是被评价对象对各等级模糊子集的隶属度，它一般是个模糊向量，而不是一个点值，因而它能提供的信息比其他方法更丰富．对多个评价对象比较并排序，就需要进一步处理，即计算每个评价对象的综合分值，按大小排序，按序择优．将综合评价结果 B 转化成综合分值，于是可依其结果进行排序，从而挑选出最优者．处理模糊综合评价向量的常用方法有以下两种：

（1）最大隶属度原则

若模糊综合评价向量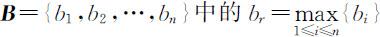 ，则被评价对象总体上来讲隶属于第r 等级，即为最大隶属原则．

（2）加权平均原则

加权平均原则就是将等级看作为一种相对位置，使其连续化．为了能定量处理，不妨用1，2，…，n 表示各等级，并称其为各等级的秩．然后用 B 中对应分量将各等级的秩加权求和，从而得到被评价对象的相对位置，其表达方式如下：

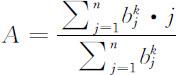
其中，k 为待定系数（k ＝1或2），目的是控制较大的b_j 所引起的作用．当k →∞时，加权平均原则就是最大隶属原则．

6.4.3　模糊综合评价法应用举例（CUMCM2005年C题）

1．问题的提出

天气对人民的生命财产及生产、生活息息相关，然而要准确、及时地对雨量做出预报十分困难．选取好的预报方法对气象部门来说是至关重要的，某气象部门正在研究6 h的雨量预报，现在他们采用2种不同的降雨量预测方法，数据已给出．该气象部门希望建立一种科学评价预报方法好坏的数学模型，来评价2种6 h雨量预报方法的准确性．气象上将6 h降雨量分为6等：0.1～2.5 mm为小雨，2.6～6 mm为中雨，6.1～12 mm为大雨，12.1～25 mm为暴雨，25.1～60 mm为大暴雨，大于60.1 mm为特大暴雨．并且要求若按此分级向公众预报，还应当在评价方法中考虑工作的感受．

2．问题的分析

我们对已给出的问题以及数据做出以下分析：我们的任务是评价该气象部门的2种雨量预报方法的优劣．首先应找出这2种方法的相同点以及不同点．由分析可知，它们是在相同时间段内，相同经度与纬度上进行气象数据采集，而所得数据不同．然后上报气象电台，经数据处理，得出6 h的雨量预报．而在向公众预报时，公众对小雨、中雨、大雨、暴雨、大暴雨的感受是一个模糊的概念，并且不同的人也会有不同的感受，但是在某一雨量域内，他们的感受应该是不会差很多的．因此我们可以建立一种模糊模型来评价这两种预报方法．

3．模型建立

问题分析时，预报小雨、中雨、大雨、暴雨、大暴雨带有模糊性，公众的感受也是模糊的．根据公众对降雨量的感受，其感受程度在其某个感受域中应符合正态分布，例如：对中雨的感受，应该以降雨量4.3 mm左右，认为是中雨的感受度最高．随着雨量的减小，远离4.3 mm时有人可能会认为是小雨；而当随着雨量增大时，远离4.3 mm，有人会认为是大雨．因此我们利用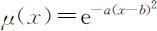 表示隶属度．据题目要求，将整个论域分为7个模糊子集，尽管气象局将降雨量划分为6个等级，但实际我们也需考虑无雨天的情况，因此我们就有7种情况需要分析．

4．建立隶属度函数模型

通过对问题的分析，我们构造了隶属度函数

上式中的x 表示降雨量，μ （x ）表示隶属度，表示在不同雨量感受域中感受半径是不相等的，因此需调整系数a，b 为雨量感受域的中心点．通过以上分析，得到以下雨量感受的模糊模型．

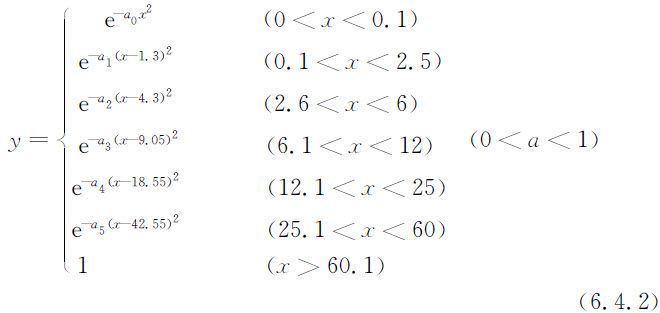
在工程中，一般隶属度为0.5时，应包含整个相应的模糊子集，故令y ＝0.5，则

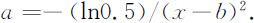
于是我们可以求出相对应的系数a_i ＝（i ＝1，2，3，4，5），于是：

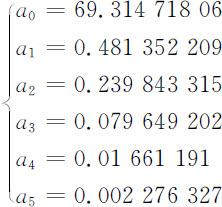
故隶属度函数模型为：

综述：将降雨量的等级分为：0～0.1 mm为无雨天气，0.1～2.5 mm为小雨，2.6～6 mm为中雨，6.1～12 mm为大雨，12.1～25 mm为暴雨，25.1～60 mm为大暴雨，大于60.1 mm为特大暴雨．各个降雨量等级分别符合上述的模糊函数．

6.5　应用举例：模糊综合评价法在堰塞湖风险评估中的应用

6.5.1　问题提出^［19］

问题要求从堰塞体危险性与溃决损失严重性两方面考虑堰塞湖风险评估问题．其中：堰塞体危险性评估依据堰塞体物质组成，堰塞体高度，堰塞湖库容，已有蓄水量4项指标；溃决损失严重性评估则依据风险人口与国民经济两项指标．

6.5.2　模型的建立与求解

1．确立风险评价指标体系

堰塞湖并不是蓄满后才溃坝，如果蓄水量只以库容为标准．把未蓄满状态作为满库考虑，就高估了实际风险相比满库状态，堰塞湖未蓄满时，可以有效减少水流对坝顶的冲刷，且对堰塞体滑移、渗透、冲刷破坏都有明显的减轻，还能继续容纳一部分降雨从而减少漫顶风险．未蓄满状态与蓄满状态的溃决可能性及溃决形式都会有所不同，所以对堰塞湖进行风险估计时，考虑已有蓄水量这一因素，应该更为准确．

从堰塞体危险性与溃决损失严重性两方面入手，分别给予评价，两者的评价结果能综合反映堰塞湖的风险状态．由问题的提出，建立堰塞湖风险评价指标体系，如表6.6所示．