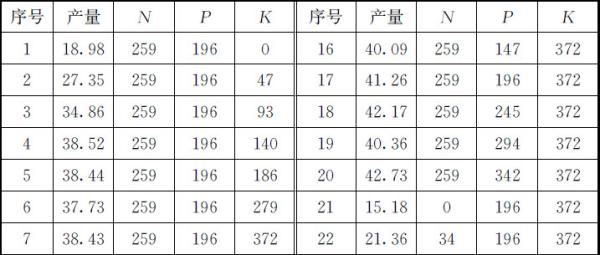
表4.1　对土豆和生菜给出的观测数据

二、回归模型的建立

在固定其他生产条件下，仅考虑施肥量与产量间的关系，用三元二次多项式进行拟合．回归模型为

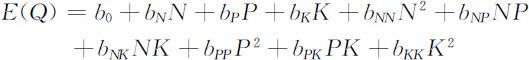
其观测为

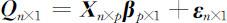
其中， Q _{n ×1} 为可观测随机向量； X _n×p 为观测阵，其中元素为原始数据中各变量及尤其生成的二次项，交互项； β _{p ×1} 为未知参数向量； ε _{n ×1} 不可观测的随机误差，服从N （0，σ ² l_n ）．

在本例中，n ＝30，p ＝10．

三、全回归模型的建立

1．数据变换

以VIF作为检验共线性影响的标准．

记 C ＝（c_ii ）（ X ^T X ）^-1 ，R （i ）为变量x_i 对其余p -1自变量的复相关系数，则有

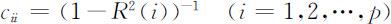
称c_ii 为变量x_i 的方差膨胀因子．一般认为，当VIF最大值接近或超过10时，共线性显著，最小二乘所得结果失真；而当均趋于1时，认为共线性影响很弱．

直接对原始数据拟合，VIF最大值接近10，故将原始数据进行相关变换．即

令

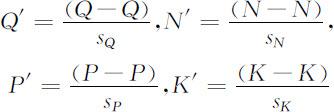
以下仍以Q，N，P，K 记标准化后的变量．

2．全回归模型

先以土豆为例．结果表明，系数矩阵不满秩，相关变换仅消除了一次项与平方项间共线性影响，而交互项仍可表示为其他项的线性组合．故仅对一次项和平方项进行回归．

（1）模型的适度性．VIF均接近于1，相关变换后的模型基本上消除了多重性影响；方差分析中，F 检验的P 值为0.0001，回归方程极其显著，真实值与回归值间R 达95.9％，拟合度极高；再由残差对观测的散点图，残差均匀分布在零值两侧，无系统偏差．因此，模型是适度的．

（2）参数估计．对回归模型的各个参数进行估计及显著性检验，结果表明，t -检验的P 值均小于0.05，参数显著不为0，含N 的参数更为显著；参数估计的方差均很小，因此参数的置信区间相对于参数值很窄（如b_NN 的95％置信区间上、下限为（-0.375899±0.0483）），参数估计有较强实用价值．

（3）相关分析．由Q 与含N 项间相关系数均很大，如与N 为0.54，与NN 为-0.62，与NK 为0.72等，知土豆产量对含N 项线性依赖性极强，而对含P 的较弱，如与P 为0.12，与PP 为0.07等．N，P，K 之间仅有极弱负相关，如N 和P 为-0.05，N 和K 为-0.05，P 和K 为-0.06．

（4）预测与回判．模型可以给出对给定N，P，K 水平下，Q 的预测值和预测区间．对原始数据作回判表明，原始数据均落在置信水平为0.95的预测区间内．

对生菜可作类似分析，其结果是：VIF接近1，方差分析中F 检验的P 值为0.0001，R 为92.7％，残差均匀分布，无系统偏向，模型适度；参数推断中，取显著性水平0.05，参数显著不为0，参数估计方差均较小，P 的作用最为显著；生菜的产量对含P 项线性依赖性极强，N，P，K 之间仅有较弱的负相关；原始数据均落在置信水平为0.95的预测区间．

从以上分析中初步得出：土豆对N依赖强，对P 弱；而生菜对P 依赖强，这与土豆是茎生长作物，需N 量高，生菜是蔬菜作物，需P 量高的规律是吻合的．