图2.14　确诊病例日增量对比图

该模型考虑的因素较为全面，能基本上反映疫情发展的本来面貌，只要给足初始值即可进行预测，不需要大量数据支持．但对疫情发展的预测不是很准确．还可用其他方法（如基于低通滤波理论的系统控制，神经网络的系统模型）加以改正．

例5　长江水质的评价和预测 （CUMCM 2005年A题）

1．问题分析

污染物浓度的变化显然随时间而变化的，这里可以考虑用微分方程来解决．由于污染物不止一种，所以要实现数据的标准化．其次建立变权函数，确定四项标准物的污染度权值；根据水质综合的指标，对长江从上游到下游的17个观测点给出每个月的水质排序．再用决策分析方法对28个月进行水质综合排序．

通常认为一个观测站（地区）的水质污染主要来自于本地区的排污和上游的污水．把7个观测站点分为6个江段，计算各江段的排污量．利用一维水质模型可以得到每个江段中污染物浓度变化，再通过假设排污口的位置，结合流量计算各江段的单位时间排污量，以此确定主要污染源所在江段．

2．模型的建立与求解

（一）问题1的模型建立与求解

（1）数据的归一化处理

①pH的谷形处理

由限值表知，对于Ⅰ～Ⅴ类地表水，p H介于6到9．在数据处理上，我们认为，由于中性液体的pH＝7，随着液体pH远离7（即大于和小于）的值的增加，其被污染的程度越大，数据处理应反映这个近似谷形关系．处理方法为

其中，P_ik 表示第i 个地区第k 个月的pH（i ＝1，2，…，17；k ＝1，2，…，28）．

②溶解氧值的归一化处理

对于污染物而言，应该遵循：值越大，污染越严重的原则．但对于溶解氧值，含量与污染度却成反向关系，因此，所选的隶属度函数必须是一个减函数．经过求解，得到所需的减函数隶属度函数为

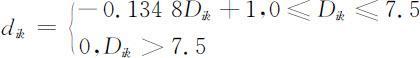
③氨氮值和高锰酸盐指数值的归一化处理

针对这两组数据的离散化程度并不是很高，可以采用极差变换法．

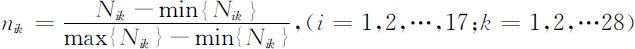
于是得到17个地区28个月的氨氮的归一化值n_ik ．同理，得高锰酸盐指数的归一化值c_ik ．

④归一化处理结果检测数据矩阵

通过上述数据的处理方法，对题中附件3的28张检测表进行处理，就能得到17个地区28个月的检测数据矩阵：

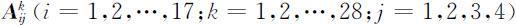
（2）变权函数的确定

分析题中附件3，发现某地区的水质类别是由溶解氧值、氨氮和高锰酸盐指数含量决定的．且由三者的最差级别决定．这种现象定义为水质类别的不越界性．定义限值表中Ⅰ～劣Ⅴ六个等级的权值分别为｛x ₁ ，x ₂ ，x ₃ ，x ₄ ，x ₅ ，x ₆ ｝，发现只要权值间满足下列关系：x ₆ ∶x ₅ ⩾2；x ₅ ∶x ₃ ⩾3，（x ₁ ，x ₂ ，x ₃ ）相互接近可以有效地防止越界的发生．

经过验证，一种可行的权值定量化为x ₃ ＝2，x ₅ ＝9，x ₆ ＝18．用变动权值的办法刻画模糊评语集｛轻度污染，中度污染，严重污染｝的等级权值．考虑到人们对于明显水质优劣有强烈的感觉，而对于同一个级别的水质类型感觉上的差异并不明显．通过心理函数，求出变动权值x ₁ ，x ₂ ，x ₄ ．综合分析选取阻滞模型，利用Matlab软件的非线性回归命令，求出曲线方程，得

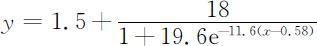
其中：y ∈x_i （i ＝1，2，…，6）表示六个等级的变动权值；x 表示经离散化后的数据．

利用上式处理限值表，得到17个地区28个月的变动权值矩阵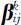 ．对权值归一化处理

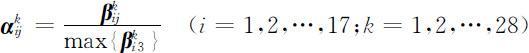
（3）17个地区28个月的水质污染值

对检测数据矩阵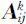 和变动权值矩阵 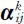进行加权求和，得到水质污染值 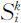为

（4）17个地区的水质综合排序

求解得17个地区28个月的水质综合排序可以得到对长江流域整体的污染程度进行更加细致的描述．现在采用决策分析中的Borda法进行水质综合排序．用Borda法处理数据，得到17个地区28个月的水质污染综合排序（见表2.2）．