4.5　常微分方程数值解

Matlab不仅可以求解常微分方程的数值解，而且可以求解简单微分方程或微分方程组的解析解（见符号处理），本节介绍数值解的求法．

4.5.1　微分方程的初始问题的数值解

微分方程的初始问题可以表示为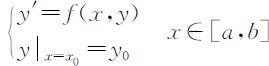 的形式，其解曲线通过点（x ₀ ，y ₀ ）的函数y ＝y （x ）．如果解析式求不出，则可以求近似数值解，即寻求解曲线上的近似点．

常微分方程数值解法的思路是：对求解区间进行剖分，利用近似公式或近似方程求解曲线在各结点的近似值．

4.5.2　欧拉法

将方程的求解区间分成n 等份，记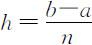 ，对于方程y ′＝f （X，y ），在x_n 处有y ′（x_n ）＝f （x_n ，y_n ）．欧拉法的基本思想是：在小区间［x_n ，x _{n ＋1} ］上用差商 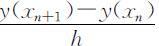代替y ′（x_n ）．此时，有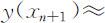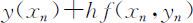： 将该公式写成递推公式：

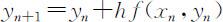称为欧拉公式或向前欧拉公式．

同样，在小区间［x_n ，x _{n ＋1} ］上用差商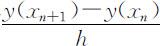 代替y ′（x_n ）可以推出：

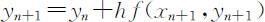称为向后欧拉公式．

向前欧拉公式和向后欧拉公式均为1阶公式，精度不高，将两个公式加起来再取平均有：

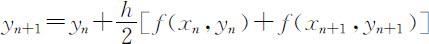称为梯形公式，可以证明，梯形公式具有2阶精度．虽然梯形公式精度稍高，但右边也有y _{n ＋1} 属于隐式公式，不能直接计算．因此可转化为：

称为改进的欧拉公式．

Matlab没有提供欧拉公式的函数，但利用上述推导，可以方便地写出改进的欧拉公式的程序．

【例】　用向前欧拉法和改进的欧拉法解初值问题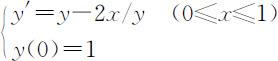 ，并与精确值比较．（取步长h ＝0.1，解析

解为 ）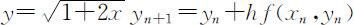

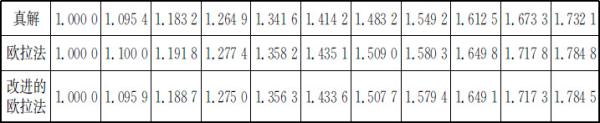
结果如下：

4.5.3　龙格—库塔法

因为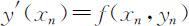 ，即f （x_n ，y_n ）表示在结点x_n 处的切线的斜率，改进的欧拉法比欧拉法精度高的原因在于，它在确定平均斜率时，多取了一个点的斜率值．这样，如果我们在区间上多取几个点的斜率值，然后对它们作线性组合得到平均斜率，则有可能构造出精度更高的计算方法．这就是龙格—库塔法的基本思想．

Matlab提供了ode23、ode45是3阶、4阶龙格—库塔法的函数．调用格式相同．

格式：［T，Y］＝ode23（′F′，TSPAN，Y0）

其中：′F′是一个字符串，是f （x，y ）的M文件．

TSPAN＝［T0 TFINAL］表示积分区间，Y0表示初始条件．

【例】　用龙格—库塔法求解：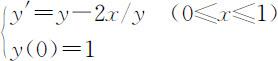

解：先将微分方程写成自定义函数exam2fun.m

function f＝exam2fun（x，y）

f＝y-2*x./y；

然后在命令窗口输入以下语句：

>>［x1，y1］＝ode23（′exam2fun′，［0：0.1：1］，1）