图2.12　人口正反馈控制系统示意图

3．人口指数

在上面的模型中密度函数p （r，t ）或分布函数F （r，t ）固然是人口发展过程最完整的描述，但是使用起来并不方便．在人口统计学中常用一些所谓人口指数来简明扼要地表示一个国家或地区的人口特征．下面是一些人口指数的定义及它们与p （r，t ）等数量之间的关系．

（1）人口总数N （t ）

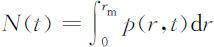
（2）平均年龄R （t ）

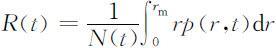
（3）平均寿命S （t ）

它表示时刻t 出生的人不论活到什么时候，死亡率都按时刻t 的μ （r，t ）计算，这些人的平均存活时间为：

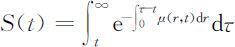
S （t ）实际上是预估寿命．通常说目前平均寿命已达到多少岁，是指今年出生婴儿的预估寿命，即S （0）．根据统计资料得到当前的死亡率μ （r ，0）后就可以算出S （0）．

（4）老龄化指数w （t ）

它定义为：

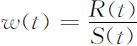
显然，平均年龄R （t ）越大，w （t ）越大；对于R （t ）相同的两个国家或地区，平均寿命S （t ）大的，表示健康水平高，一个人能工作的时间在一生中占的比例大，于是老龄化指数w （t ）较小．

鉴于我国目前人口的年龄结构状况，在控制生育率、降低人口增长速度的同时，需适当考虑不要使老龄化指数变得过高．

（5）依赖性指数ρ （t ）

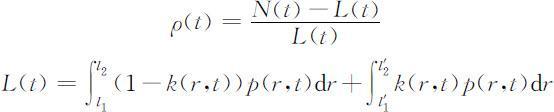
其中［l ₁ ，l ₂ ］和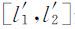 分别是男性和女性有劳动能力的年龄区间，L （t ）是全体人口中有劳动能力的人数，所以依赖性指数ρ （t ）表示平均每个劳动者要供养的人数．

例3　按年龄分组的种群增长

当某个自然环境中只有一种生物的群体（生态学上称为种群）生存时，人们常用阻滞增长模型来描述这个种群数量的演变过程，即

x （t ）是种群在时刻t 的数量，r 是固有增长率，N 是环境资源容许的种群最大数量．由（2.3.29）式可以直接得到：x ₀ ＝N 是稳定平衡点，即t →∞时，x （t ）→N ．

在组织增长模型中，它没有考虑种群的年龄结构，种群的数量主要是由总量的固有增长率决定的．显然，不同年龄动物的繁殖率和死亡率有着明显的不同，为了更精细地预测种群的增长规律，本节讨论按年龄分组的种群增长预测模型．这个向量形式的差分方程是Leslie在20世纪40年代用来描述女性人口变化规律的．

下面先建立差分方程模型，接着讨论稳定状况（即时间充分长）下种群的增长规律，然后分析各年龄组的繁殖率和死亡率对种群总量增减的影响．

1．模型建立

将种群按年龄大小等间隔地分成n 个年龄组，比如每10岁或每5岁为1个年龄组．与年龄的离散化相对应，时间也离散为时段，并且时段的间隔与年龄区间大小相等，即以10年或5年为1个时段．

种群是通过雌性个体的繁殖而增长的，所以用雌性个体数量的变化为研究对象比较方便，下面提到的种群数量均仅指其中的雌性．

记时段k 第i 年龄组的种群数量为x_i （k ），k ＝0，1，2，…；i ＝1，2，…，n ，第i 年龄组的繁殖率为b_i ，即第i 年龄组的每个（雌性）个体在1个时间段内平均繁殖的数量，第i 年龄组的死亡率为d_i ，即第i 年龄组1个时间段内死亡数与总数之比．s_i ＝1－d_i 称为存活率．这里假设b_i 和d_i （从而s_i ）不随时段k 变化，在稳定的环境下这个假设是合理的．b_i 和s_i 可由统计资料获得．x_i （k ）的变化规律由以下的基本事实得到：时段k ＋1第1年龄组种群组数量是时段k 各年龄组繁殖数量之和，即

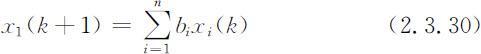
时段k ＋1第i ＋1年龄组的种群数量是时段k 第i 年龄组存活下来的数量．即

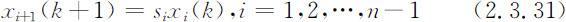
记时段k 种群按年龄组的分布向量为：

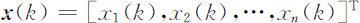
由繁殖率b_i 和存活率s_i 构成的矩阵

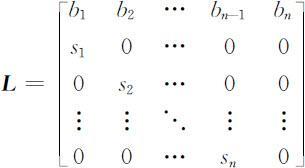
则（2.3.30）式和（2.3.31）式可表示为：

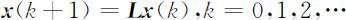
当矩阵 L 和按年龄组的初始分布向量 x （0）已知时，可以预测任意时段k 种群按年龄组的分布为：

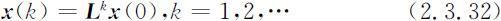
有了 x （k ），当然不难算出时段k 种群的总数．

2．稳定状况分析

下面研究时间充分长后（即k →∞）种群的年龄结构及数量的变化．

根据b_i 和s_i 的定义，矩阵 L 中的元素满足：

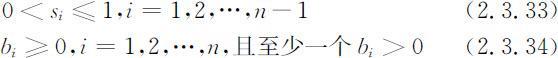
注：在（2.3.33）式中，若某个s_i ＝0，那么第三年龄组应取消．满足（2.3.33）和（2.3.34）两个式子的矩阵 L 称Leslie矩阵（简称 L 矩阵）．容易看出，x （k ）的稳定性完全由矩阵决定．关于 L 矩阵我们不加证明地叙述两个定理．

定理1　L 矩阵有唯一的正特征值λ ₁ ，且它是单重的，λ ₁ 对应正特征向量

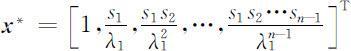
L 矩阵的n －1个其他特征值λ_k 都满足：

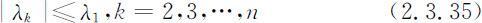
该定理表明 L 矩阵的特征方程为：

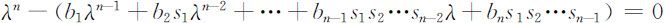
只有一个正单根λ ₁ ，且容易验证 L x ＝λ ₁ x ．

定理2 　若 L 矩阵第一行有两项顺次的元素b_i ，b _{i ＋1} 都大于零，则（2.3.35）式中仅不等号成立，即

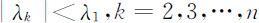
且由（2.3.32）式表示的 x （k ）满足：

其中c 是由b_i ，s_i 及 x （0）决定的常数．

附带指出，对于种群增长来说该定理的条件通常是满足的．

从上述定理可以对时间充分长（k 充分大）时种群按年龄组的分布 x （k ）的性态作出如下分析．（为简便起见将λ ₁ 记为λ ）

①由（2.3.36）式直接有：

这说明：k 充分大时种群按年龄组的分布 x （k ）趋向于稳定，其各年龄组的数量占总量的比例，与特征向量 x 中对应分量占总量的比例是一样的，即 x 就表示了种群按年龄组的分布状况，故 x ^* 可称为稳定分布，它与初始分布 x （0）无关．

②由（2.3.37）式又可以得到：

或者更清楚的写作：

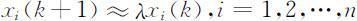
这表明：k 充分大时种群的增长也趋向稳定，其各年龄组的数量都是上一时段同一年龄组数量的λ 倍，即种群的增长完全由 L 矩阵的唯一正特征根决定．显然，当λ >1时，种群递增；当λ <1时，种群递减．λ 可称为固有增长率．

③λ ＝1时种群数量不变．由 L 矩阵的特征方程可知这个条件等价于：

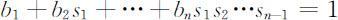
若将上式左端记作：

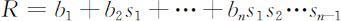
由这个表达式可以知道：R 表示一个（雌性）个体在整个存活期内繁殖的平均数量，称为总和繁殖率，显然R ＝1时，种群总量不变．由定理1中 L 矩阵的正特征值λ ₁ 对应的特征向量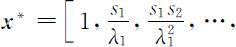 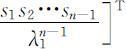可知，此时稳定分布为：

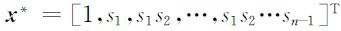
根据（2.3.37）式，这个结果表明：

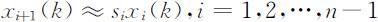
即当k 充分大且R ＝1时，存活率s_i 等于相邻两年龄组的种群数量x _{i ＋1} （k ）与x_i （k ）之比．

3．人口模型（离散型）

在例1中我们讨论过连续形式的人口模型，如将其中给出的生育率、生育模式等概念引入到Leslie模型中，即满足：

于是可以得到离散形式的人口模型^［20］ ．

为方便起见，这里只涉及女性人口（只要考虑性别比函数即可得到总人口数），且以1岁为1个年龄组，1年为1个时段，即k 年i 岁的女性人数为x_i （k ）．设生育率与年龄和时间有关，记k 年i 岁女性生育率（每位女性平均生育的女儿数）为b_i （k ），育龄区间为［i ₁ ，i ₂ ］．设死亡率只与年龄有关，记i 岁女性死亡率为d_i ，存活率为s_i ．

进一步将b_i （k ）分解为：

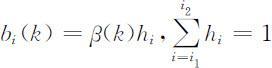
其中h_i 为生育模式，而β （k ）满足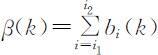： ，是k 年所有育龄女性平均生育的女儿数，若女性在育龄期所及的时间内保持生育率不变，则β （k ）就是k 年i ₁ 岁的每位女性一生平均生育的女儿数，即总和生育率（或生育胎次），是控制人口数量的主要参数．

仍用 x （k ）表示女性人口的（按年龄）分布向量，即 x （k ）＝［x ₁ （k ），x ₂ （k ），…，x_n （k ）］^T ，为了清楚地表明β （k ）的作用，将 L 矩阵分解为：

则模型（2.3.38）式应表示为：

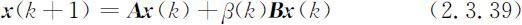
当根据统计资料知道了人口的初始分布x （0）和存活率矩阵 A ，并给定了生育模式矩阵 B ，就可以用不同的总和生育率β （k ）来预测或控制未来的人口数量．

在控制理论中 x （k ）为状态变量，β （k ）为控制变量，（2.3.39）式对于 x （k ）和β （k ）都是双线性的，称双线性方程．

类似地，对人口总数，平均年龄，平均寿命等，可进行离散化，引入离散形式模型的人口指数．

离散形式模型的优点是便于计算机作数值计算，20世纪70年代末曾用这类模型，根据1978年的统计资料对21世纪我国人口总数作预测．在不同的总和生育率β 下得到了1980～2080年一系列结果．图2.13是这些结果的略图．计算结果表明：