6.3　三维图形

6.3.1　空间参数曲线

6.3.2　带网格的曲面

A．水平面格点数据生成函数（meshgrid）

设空间坐标系为xyz（x横坐标，y纵坐标，z立坐标），在x轴上有一个剖分，在x轴的剖分点上作与y轴的平行线．y轴上一个剖分，在y轴上的剖分点作与x轴的平行线．这样构成一个网格，这些网格点向z轴寻找曲面上的点构成了空间曲面．

格式1：［X，Y］＝meshgrid（x，y）

注1：这里x，y是一个向量，x表示在x轴上的一个剖分，y表示在y轴上的一个剖分；

注2：X是函数meshgrid返回的一个矩阵，表示xy平面上所有网格点的x坐标值，Y是函数meshgrid返回的一个矩阵，表示xy平面上所有网格点的y坐标值．

格式2：［X，Y］＝meshgrid（t）这里t是一个向量，这个格式表示坐标轴x轴与y轴的剖分相同，均按t进行．

B．网格图绘制

格式1：mesh（X，Y，Z）和surf（X，Y，Z）这里X，Y是按meshgrid生成的矩阵格式，Z是曲面函数在X，Y中的值，即：X，Y，Z是各点坐标的横、纵、立坐标构成的矩阵.mesh主要偏重网格图，surf主要偏重表面图．Z既指定了曲面的颜色，也指定了曲面的高度，所以渐变的颜色可以和高度适配．

【例】　作图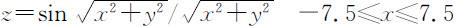

解：

>>x＝-7.5：0.2：7.5；％剖分，注意定义域，剖分要避开（0，0）点

>>y＝x；

>>［X，Y］＝meshgrid（x，y）；％生成格点矩阵数据

>>R＝sqrt（X.^2＋Y.^2）；

>>Z＝sin（R）./R；％计算立坐标矩阵

>>mesh（X，Y，Z）％绘制网格图

格式2：meshc（X，Y，Z）和surfc（X，Y，Z）在mesh函数的作用之上增加了绘制带有等高线．

格式3：meshz（X，Y，Z）和surfl（X，Y，Z）在mesh函数的作用之上增加了屏蔽作用，即增加了边界面屏蔽．