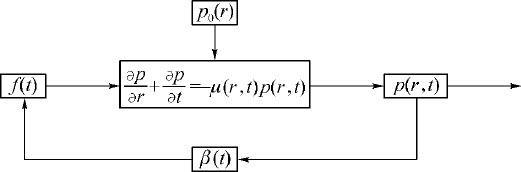
图2.9　SIR模型的相轨线

若记t →∞时，s （t ）、i （t ）和r （t ）的极限值分别为s _∞ 、i _∞ 和r _∞ ．下面根据（2.3.14）式，（2.3.17）式和图2.9来分析s （t ）、i （t ）和r （t ）的变化情况，得到如下四个结论．

结论1：不论初值条件s ₀ 和i ₀ 如何，病人终将消失，即：

证明：首先由（2.3.14）式可知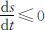： ，而s （t ）⩾0，故s _∞ 存在．由（2.3.13）式可知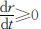： ，而r （t ）⩽1，故r _∞ 存在；再由（2.3.12）式，知i _∞ 存在．下面证其极限为0．假设极限不为0，而是r _∞ ＝ε >0，则由（2.3.12）式，对于充分大的t 有 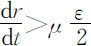，这将导致r _∞ ＝∞，矛盾，故i _∞ ＝0．

从图形上看，不论相轨线从P ₁ 点还是P ₂ 出发，它终将和s 轴相交（当t 充分大时）．

结论2：最终未被感染的健康者的比例s _∞ 满足如下方程（在（2.3.17）式中令i ＝0）：

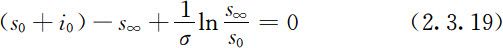
且s _∞ ∈（0，1／σ ）．从图2.9中可以看出，s _∞ 是相轨线与s 轴在（0，1／σ ）内交点的横坐标．

结论3：若s ₀ >1／σ ，则i （t ）先增加，当s ＝1／σ 时，i （t ）达到最大值：

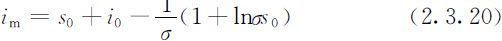
然后，i （t ）减少且趋于零，s （t ）则单调减小到s _∞ ，如图2.9中P ₁ （s ₀ ，i ₀ ）出发的轨线．

结论4：若s ₀ ⩽1／σ ，则i （t ）单调减少至零，s （t ）则单调减小到s _∞ ，如图2.9中P ₂ （s ₀ ，i ₀ ）出发的轨线．

可以看出，如果仅当病人比例i （t ）有一段增长的时期才认为传染病在蔓延，那么1／σ 是一个阈值，当s ₀ >1／σ （即σ >1／s ₀ ）时传染病就会蔓延．而减少传染期接触数σ ，即提高阈值1／σ ，使得s ₀ ⩽1／σ （即σ ⩽1／s ₀ ），传染病就不会蔓延（健康者比例的初值s ₀ 是一定的，通常可认为s ₀ 接近于1）．

并且，即使s ₀ >1／σ ，从（2.3.19）式和（2.3.20）式也可以看出来，σ 减小时，s _∞ 增加（通过作图分析），i _m 降低，也控制了蔓延的程度．我们注意到σ ＝λ ／μ 中，人们的卫生水平越高，日接触率λ 越小；医疗水平越高，日治愈率μ 越大，于是σ 越小，所以提高卫生水平和医疗水平有助于控制传染病的蔓延．

从另一方面看，σs ＝λs ·1／μ 是传染期内一个病人传染的健康者的平均数，称为交换数，其含义是一个病人被σs 个健康者交换．所以，当s ₀ ⩽1／σ （即σs ₀ ⩽1）时，必有σ s⩽1．既然交换数不超过1，病人比例i （t ）绝不会增加，传染病不会蔓延．

5．控制传染病蔓延方法

根据对SIR模型的分析，当s ₀ ⩽1／σ 时，传染病不会蔓延．所以，针对s ₀ 和1／σ 这两个方面，为了制止传染病的蔓延，有两种控制的方法．

第一种方法是：使1／σ 尽量大，即提高卫生和医疗水平；第二种方法是：使s ₀ （健康人比例的初始值）尽量小，这可以通过预防接种，使群体免疫的办法做到．

忽略病人比例的初始值i ₀ ，有s ₀ ＝1－r ₀ ，于是s ₀ ⩽1／σ 可以表示为：

这就是说，只要通过群体免疫使初始时刻的移出者比例（即免疫者比例）r ₀ 满足（2.3.21）式，就可以制止传染病的蔓延．

本节介绍的传染病模型从几个方面很好地体现了模型的改进、建模的目的性，以及方法的配合．

第一，最初建立的模型Ⅰ基本上不能用，修改假设后得到的SI模型，虽有所改进，但仍不符合实际．进一步修改假设，并针对不同情况建立了SIS模型和SIR模型，这两种模型才是比较符合实际的．

第二，SIS模型和SIR模型的可取之处在于它们比较全面的达到了建模的目的，即描述传播过程、分析受感染的人数变化规律，预测传染病高潮到来的时刻，度量传染病蔓延的程度，并探索制止蔓延的手段．

第三，对于比较复杂的SIR模型，采用了数值计算方法，图形观察与理论分析相结合的方法，先有感性认识（表2.1，图2.7，图2.8），再用相轨线做理论分析．可以看作是计算机技术与建模方法的巧妙配合．

例2　人口的预测和控制（连续模型）

人口问题是当今世界上最令人关注的问题之一．一些发展中国家的人口出生率过高，越来越严重地威胁着人类的正常生活，有些发达国家的自然增长率趋近于零，甚至是负数，造成劳动力短缺，也是不容忽视的问题．由于我国20世纪五六十年代人口政策方面的失误，造成人口总数增长过快，使得年龄结构不合理，对人口增长的严格控制会导致人口老龄化问题严重．因此在首先保证人口有限增长的前提下适当控制人口老龄化，把年龄结构调整到合适的水平，是一项长期而又艰巨的任务．

建立数学模型对人口发展过程进行描述、分析和预测，并进而研究控制人口增长和老龄化的生育策略，已引起社会各方面的极大关注，是数学在社会发展中的重要应用领域．我国一些从事自然科学，主要是控制论研究的专家，从我国人口的现状出发，结合当前的人口政策，在人口预测和控制方面做了许多工作．这里介绍的人口模型包含了他们的部分（也是基本的）成果^［20］ ．

模型中不但要考虑人口总数、总的增长率，还要考虑年龄结构，因为不同年龄人的生育率和死亡率有着很大的差别．两个国家或地区目前人口总数一致，如果一个国家或地区年轻人的比例高于另一个国家或地区，那么两者人口的发展状况将大不一样．所以模型中要考虑人口按年龄的分布，即除了时间变量外，年龄也是另一个自变量．

1．人口发展方程

使人口数量和结构变化的因素不外乎出生、死亡和迁移．为简化起见，这里只考虑自然的出生和死亡，不计迁移等社会因素的影响．

为研究任意时刻不同年龄的人口数量，引入人口的分布函数和密度函数．时刻t 年龄小于r 的人口称为人口分布函数，记作F （r，t ），其中r，t （⩾0）均为连续变量，设F （r，t ）是连续、可微的．时刻t 的人口总数记作N （t ），最高年龄记作r _m ，理论推导时设r _m →∞．于是对于非负非降函数F （r，t ），有

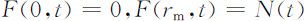
人口密度函数定义为：

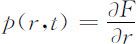
p （r，t ）dr 表示时刻t 年龄在区间［r，r ＋dr ）内的人数．

记μ （r，t ）为时刻t 年龄r 的人的死亡率，则μ （r，t ）p （r，t ）dr 表示时刻t 年龄在［r，r ＋dr ）内单位时间死亡的人数．

为了得到p （r，t ）满足的方程，考察时刻t 年龄在［r，r ＋dr ）内的人到时刻t ＋dt 的情况．他们中活着的那一部分人的年龄变为［r ＋dr ₁ ，r ＋dr ＋dr ₁ ），这里dr ₁ ＝dt ．而在dt 这段时间内死亡的人数为μ （r，t ）p （r，t ）dr dt ．于是：

p （r，t ）dr －p （r ＋dr ₁ ，t ＋dt ）dr ＝μ （r，t ）p （r，t ）dr dt

上式可写为：

［p （r ＋dr ₁ ，t ＋dt ）－p （r，t ＋dt ）］dr ＋［p （r，t ＋dt ）－p （r，t ）］dr ＝－μ （r，t ）p （r，t ）dr dt

注意到：dr ₁ ＝dt ，就可以得到：

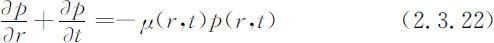
这是人口密度函数p （r，t ）的一阶偏微分方程，其中死亡率μ （r，t ）为已知函数．

方程（2.3.22）有两个定解条件：初始密度函数记作p （r ，0）＝p ₀ （r ）；单位时间出生的婴儿数记作p （0，t ）＝f （t ），称婴儿出生率．p ₀ （r ）可由人口调查资料得到，是已知函数；f （t ）则对预测和控制人口起着重要作用，后面将对它进一步分析，将方程（2.3.22）及定解条件写为：

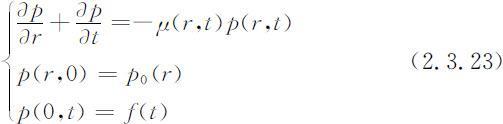
这个连续型人口发展方程描述了人口的演变过程，从这个方程确定出密度函数p （r，t ）以后，立即可以得到各个年龄的人口数，即人口分布函数：

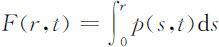
方程（2.3.23）的求解过程比较复杂，这里只给出一种特殊情况下的结果．在社会安定的局面下和不太长的时间内，死亡率大致与时间无关，于是可近似地假设μ （r，t ）＝μ （r ）．这时（2.3.23）式的解为：

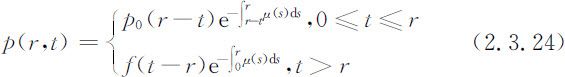
显然（2.3.24）式满足（2.3.23）式，其解见图2.10所示．这个解在rOt 平面上有一个浅显的解释：

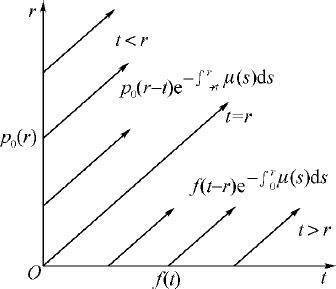
图2.10　rOt 平面上的p （r，t ）

对角线t ＝r 将rOt 平面分成两部分，在t <r 区域，p （r，t ）完全由年龄为r －t 的人口初始密度p ₀ （r －t ）和这些人的死亡率μ （s ）（r －t ⩽s ⩽r ）决定；而在t >r 区域，p （r，t ）则由未来的生育状况f （t －r ）和死亡率μ （s ）（0⩽s ⩽r ）决定．

2．生育率和生育模式

在方程（2.3.23）式或解（2.3.24）式中，p ₀ （r ）和μ （r ）可从人口统计数据得到，μ （r，t ）也可由μ （r ，0）粗略估计．这样，为了预测和控制人口的发展状况，人们主要关注和可以用作控制手段的就是婴儿出生率f （t ）了．下面对f （t ）作进一步分解．

记女性性别比函数为k （r，t ），时刻t 年龄在［r，r ＋dr ）的女性人数为k （r，t ）p （r，t ）dr ，将这些女性在单位时间内平均每人的生育数记作b （r，t ），设育龄区间为［r ₁ ，r ₂ ］，则：

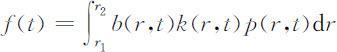
再将b （r，t ）定义为：

其中h （r，t ）满足：

于是：

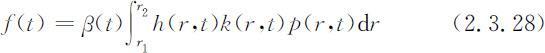
由（2.3.27）式可以看出，β （t ）的直接含义是时刻t 单位时间内平均每个育龄女性的生育数．如果所有育龄女性在其育龄期所及的时刻都保持这个生育数，那么β （t ）也表示平均每个女性一生的总和生育数，所以，β （t ）称为总和生育率（简称生育率）或生育胎次．

从（2.3.25）和（2.3.26）两式及b（r，t ）的含义可以看出，h （r，t ）是年龄为r 女性的生育加权因子，称生育模式．在稳定环境下可以近似地认为它与t 无关，即h （r，t ）＝h （r ）．h （r ）表示了在哪些年龄生育率的高低．图2.11给出了h （r ）的示意图，表明r ＝r ₀ 附近生育率最高．由人口统计资料可以知道当前实际的h （r，t ）．作理论分析时人们常采用的h （r ）的一种形式是借用概率论中的Γ 分布：

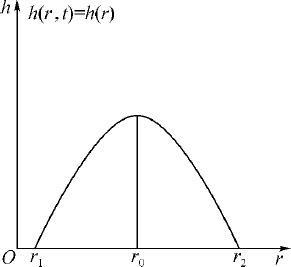
图2.11　生育模式h （r ）示意图

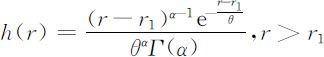
并取θ ＝2，α ＝n ／2，这时有：

r ₀ ＝r ₁ ＋n －2

可以看出，提高r ₁ 意味着晚婚，而增加n意味着晚育．

这样，人口发展式（2.3.23）和单位时间出生的婴儿数f （t ）的表达式（2.3.28），构成了我们的连续型人口模型．模型中死亡率函数μ （r，t ）、性别比函数k （r，t ）和初等密度函数p ₀ （r ）可以由人口统计资料直接得到，或在资料的基础上估计，而生育率β （t ）和生育模式h （r，t ）则是可以用于控制人口发展过程的两种手段．β （t ）可以控制生育的多少，h （r，t ）可以控制生育的早晚和疏密．我国的计划生育政策正是通过这两种手段实施的．

这样，人口发展式（2.3.23）和单位时间出生的婴儿数f （t ）的表达式（2.3.28），构成了我们的连续型人口模型．模型中死亡率函数μ （r，t ）、性别比函数k （r，t ）和初等密度函数p ₀ （r ）可以由人口统计资料直接得到，或在资料的基础上估计，而生育率β （t ）和生育模式h （r，t ）则是可以用于控制人口发展过程的两种手段．β （t ）可以控制生育的多少，h （r，t ）可以控制生育的早晚和疏密．我国的计划生育政策正是通过这两种手段实施的．

从控制论观点看，在方程（2.3.23）描述的人口系统中p （r，t ）可视为状态变量，p （0，t ）＝f （t ）视为控制变量，是分布参数系统的边界控制函数．（2.3.28）式表明控制输入中含有状态变量，形成状态反馈，β （t ）视为反馈增益．并且通常是一种正反馈，即人口密度函数p （r，t ）的增加，通过婴儿出生率f （t ）又使p （r，t ）进一步增大（见图2.12）．方程的解（2.3.24）式中因子f （t －r ）表明这种反馈还有相当大的滞后作用，所以一旦人口政策失误，使p （r，t ）在一段时间内增长得过多过快，再想通过控制手段β （t ）和h （r，t ）把人口增长的势头降下来，就很困难并且常常需要相当长（几代人）的时间．